基于样本熵的时间序列非线性检测方法研究
2014-12-23李聪改
李聪改,曹 锐,武 政,相 洁,2
(1.太原理工大学 计算机科学与技术学院,山西 太原030024;2.北京工业大学 国际WIC研究院,北京100000)
0 引 言
对于生理信号等观测得到的时间序列,目前常用于检验其非线性特性的方法主要是替代数据法。替代数据法最早是在1992年由Theiler等人提出,之后很多学者对该方法提出了改进[3-9]。用于验证原数据和替代数据之间差别的特 征 量 有 很 多,如 关 联 维D2[10-12]、近 似 熵 (approximate entropy,ApEn)[13-16]等。然而,这些指标都存在一些不足,如使用关联维时,只有数据量很大时才能得到可靠结论[17]。近似熵的结论也缺乏相对一致性[18],且计算时间较长。样本熵 (sample entropy,SampEn)是近似熵算法的改进,比近似熵具有更好的稳定性。样本熵是否可以作为特征量来判定时间序列的非线性特性?本文针对这一问题进行了相关研究,文中将样本熵作为替代数据法中的特征量,在3种仿真时间序列上验证样本熵是否可以作为特征量来识别时间序列的非线性特性。本文同时也记录了近似熵作为特征量的实验结果,并对近似熵和样本熵的结果进行了对比。
1 基于样本熵的替代数据法
1.1 替代数据分析方法
替代数据法中,首先提出零假设 (假设原始待测数据是线性的),其次通过振幅调节傅里叶变换 (AAFT)等方法产生替代数据。替代数据是随机排列的线性数据,它与原始数据具有相同的功率谱,但是,原始数据中的非线性成分已经被完全破坏掉了。产生替代数据之后,分别计算原始数据与替代数据的特征量,并采用如式 (1)所示的统计检验方法来比较原始数据和替代数据之间的差异,如果原始数据与替代数据特征量差别显著,则拒绝原假设,即原始时间序列为非线性;反之为线性

式中:Ao——原始数据的某特征量的值,As——多组替代数据的该特征量的平均值,SD(As)——多组替代数据的该特征量的标准差。
1.2 样本熵
样本熵SampEn是由Richman和Moorman提出的一种新的时间序列复杂性测度方法[19],是ApEn的一种改进算法,其计算方法如下:
步骤1 将序列x(1),x(2),...,x(N)按顺序组成m维矢量,即
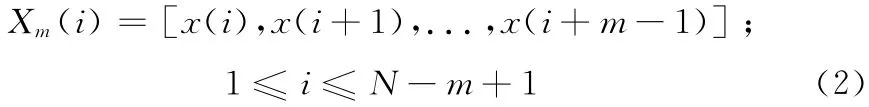
步骤2 定 义Xm(i)与Xm(i)间 的 距 离d[Xm(i),Xm(i)]为两者对应元素中差值最大的一个,即
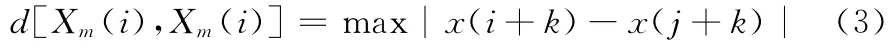
式中:1≤k≤m-1;1≤i,j≤N-m+1,i≠j。
步骤3 给定的阈值r(r>0),对每一个1≤i≤Nm 值统计d[Xm(i),Xm(i)]<r 的数目 (称之为模板匹配数)与总的距离数目N-m-1的比值,记作Bmi(r)

其中1≤j≤N-m,j≠i。求其对i所有的平均值
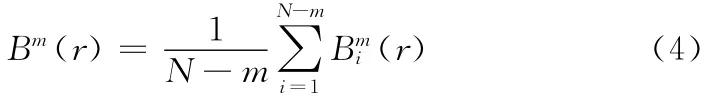
对于m+1点矢量,同样有
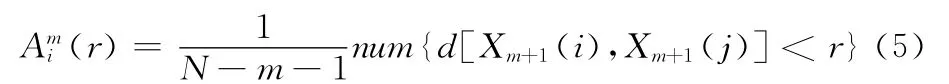
其中1≤j≤N-m,j≠i。求其对所有i的平均值
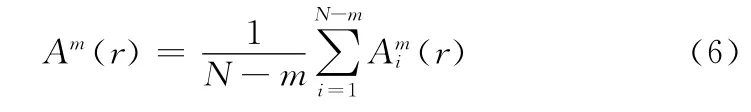
步骤4 此序列的样本熵为

但是在实际计算中N 不可能为∞,当N 取有限值时,估计

样本熵的算法思想是:当维数为m 时,时间序列的自相似概率用B 表示;当维数为m+1 时,时间序列的自相似概率用A 表示,从而可以得出公式:CP=A/B。可以看出,样本熵的计算是以-ln (CP)为模型。近似熵的算法与样本熵类似,但是近似熵的计算过程中对数据自身进行了匹配,因而在计算的过程中肯定会存在偏差。另外近似熵的值与相似容限r的取值有很大关系,导致对于不同的参数计算结果缺乏相对一致性。因此本文提出将近似熵的改进算法—样本熵作为特征量引入到替代数据法中来检验时间序列的非线性特征。
2 仿真数据
本文实验所采用的数据为线性AR 模型、Lorenz方程、Logistic方程所产生的时间序列。其中线性AR 模型产生的时间序列确定是线性的;Lorenz方程产生的是典型的连续的非线性时间序列;而Logistic方程产生的是典型的离散的非线性时间序列。实验将验证本文提出的基于样本熵的非线性检测方法对这3种时间序列的检测结果是否与时间序列原特性一致。
为了验证SampEn作为特征量时,是否如关联维D2一样会受到时间序列长度的影响,实验中采用8种不同的时间长度的序列。同时,为了避免计算结果的偶然性,仿真实验为每个时间长度均产生了20组原始数据。另外,实验中记录了SampEn与ApEn作为特征量进行非线性检测时的运算时间,并进行了对比。
2.1 非线性数据
本文中采用两种方程来产生确定性混沌的时间序列:利用Lorenz方程产生连续的非线性时间序列,用Logistic方程产生离散的非线性时间序列。
Lorenz方程公式如下所示

当参数σ=10;r=28;b=8/3时,方程产生的数据为非线性。
产生非线性数据的Logistic离散映射方程如下所示
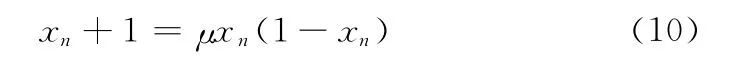
当μ=4.0,初始值x (1)=0.1的时候,产生的数据为非线性。
2.2 线性数据
本文采用一阶自回归AR 模型来产生线性数据,其计算方法如下所示

式中:e(t)——白噪声,服从均值为0,方差σ2的分布。论文中,取系数k=0.2,取初始值y(1)=0,e(t)的均值为0,方差为1。
为了避免数据的随机性,实验中首先对上述3种待测数据分别产生长度为5000 的数据,分别随机选择长度为100,200,300,500,800,1000,2000,3000 的数据 各20次作为原始数据并计算特征量,其次对每个长度下每组原始数据分别产生20组替代数据,并求得20组替代数据的特征量,最后计算得到原始数据和替代数据特征量的差别显著度。ApEn 和SampEn 的计算过程中,涉及到参数m,r的选取。根据参考文献 [19],本文计算过程中,维数m=2,相似容限r=0.15SD (SD 为时间序列的标准差)。
3 实验结果及分析
3.1 Lorenz
实验计算了8 种长度数据的特征量,图1 (a)、图1(b)仅给出数据长度N 分别为300和800时第1次产生的原始数据和对应的20组替代数据的样本熵值分布情况,其它长度结果类似。其中,横坐标sur表示第几组替代数据,纵坐标SampEn表示该数据的样本熵值。“+”表示原始数据的样本熵,“*”表示替代数据的样本熵。从图1中可以看出,本次原始数据的熵值和替代数据的熵值存在差异。所有数据的差别显著度结果见表1。
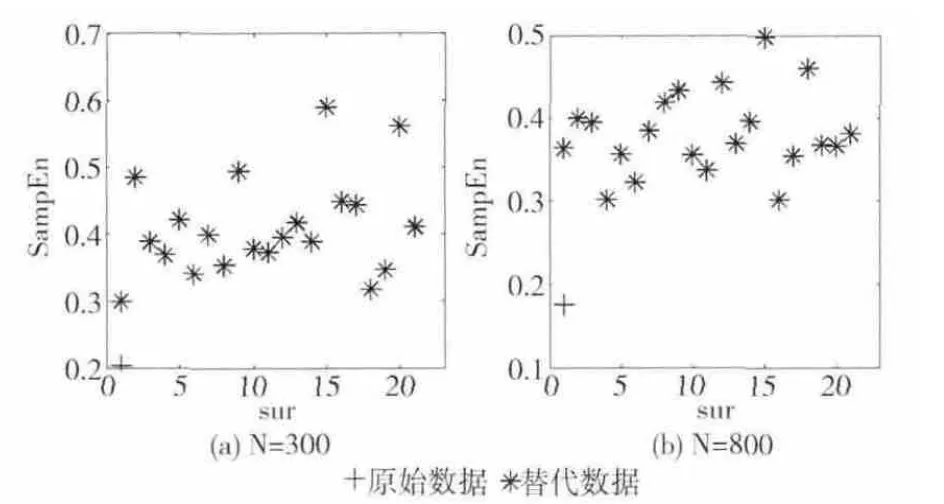
图1 Lorenz时间序列样本熵结果分布
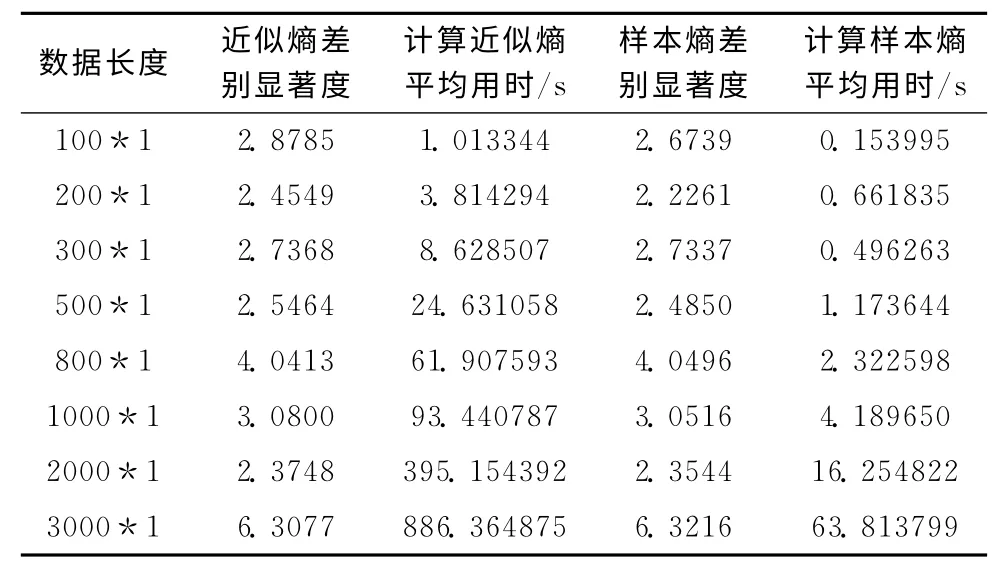
表1 Lorenz方程产生数据的熵值比较(df=19,ɑ=95%)
从表1中可以看出,所有差别显著度值均大于2.093(df=19,ɑ=0.95时的t检验临界值),意味着所有的差别显著度均达到了统计检验显著性,无论近似熵还是样本熵都可以判断出原始时间序列中包含非线性成分 (和Lorenz时间序列已知特性相符)。此外,不同长度下非线性检测的结果稳定,表明非线性检测结果不受数据长度的影响,并且样本熵的计算用时比近似熵大幅度减少。
3.2 Logistic离散映射
对于Logitic方程产生的时间序列,同样进行了相关处理并给出了实验结果。图2 (a)、图2 (b)也仅给出数据长度N 分别为300和800时第1次产生的原始数据和对应的20组替代数据的样本熵值分布情况。所有数据的差别显著度结果见表2。
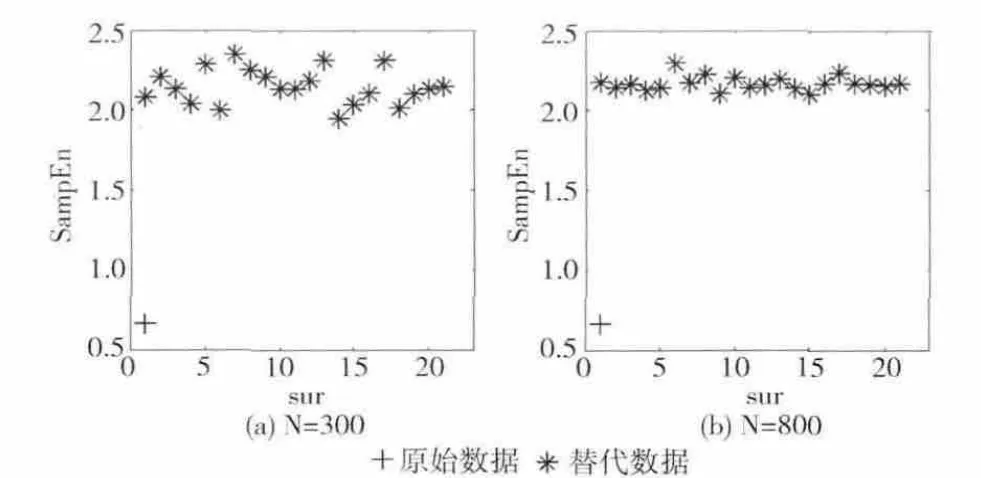
图2 Logistic时间序列样本熵结果分布
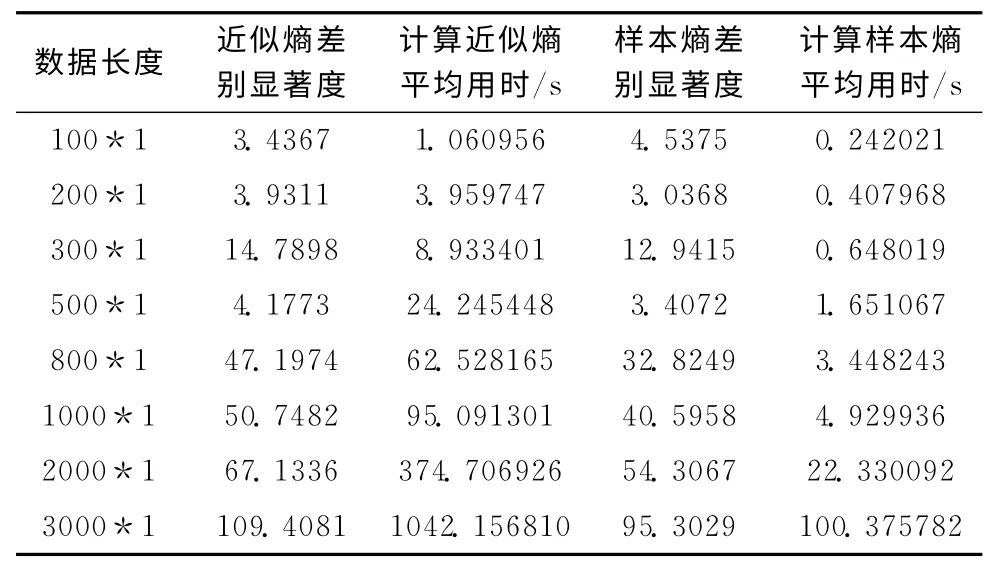
表2 Logistic方程产生数据的熵值比较(df=19,ɑ=95%)
从表2中可以看出,Logistic数据与Lorenz数据的实验结果类似,所有的差别显著度值均大于2.093 (df=19,α=0.95时的t检验临界值),表明样本熵作为特征值同样可以检测出待测数据中包含了非线性的成分 (和Logistic时间序列已知特性相符),并且不受数据长度的影响,以及计算用时比近似熵短。
3.3 一阶自回归AR 模型

图3 线性AR 时间序列样本熵结果分布
同前两个实验一样,本次也计算了AR 模型产生的8种长度数据的特征量,图3 (a)、图3 (b)仅给出数据长度N 分别为300和800时第1次产生的原始数据和对应的20组替代数据的样本熵值分布情况,其它长度结果类似。但图3 (a)、图3 (b)中可以看出,本次20组替代数据的熵值分布在原始数据的熵值周围,并没有出现像图1和图2中熵值的分离情况,意味着这组原始数据与替代数据并没有显著的差异。所有数据的差别显著度结果见表3。
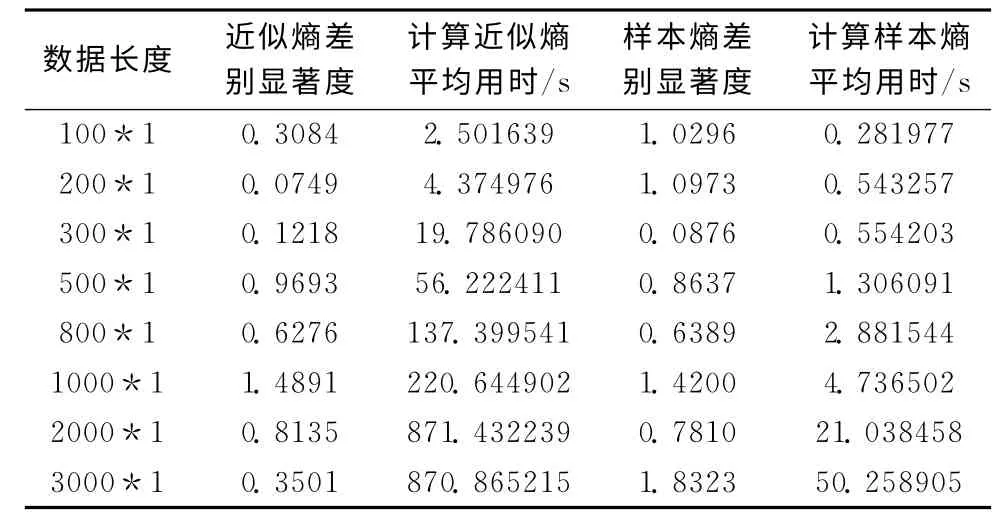
表3 一阶自回归模型产生数据的两种熵值比较(df=19,ɑ=95%)
表3中所有的差别显著度值均小于2.093 (df=19,α=0.95时的t检验临界值),表明原始数据与替代数据近似熵与样本熵的值的差异没有达到统计检验显著性,即原始数据和替代数据不存在显著差异,可以判断该时间序列中不包含非线性成分,是线性的 (和AR 时间序列已知特性相符),并且该结果不受数据长度的影响,另外样本熵计算用时比近似熵要短。
在本实验中,通过替代数据法对不同长度的时间序列进行了非线性检测。实验结果表明,近似熵和样本熵这两个指标均可作为替代数据法的特征量,较好的验证时间序列中的非线性成分。但是在相同长度的时间序列上,样本熵的用时要比近似熵短。
基于关联维的时间序列非线性检测对数据长度要求较高,本实验通过8种数据长度分析了样本熵作为特征量检验非线性特征时是否依赖于数据长度。结果表明样本熵作为特征量时对数据长度要求不高,适合较短时间序列的非线性特性检测。
4 结束语
论文在三组仿真数据上,验证了样本熵是否可以作为特征量来验证时间序列中有无非线性成分。实验结果表明,对于不同长度的时间序列,样本熵均可以作为替代数据法的特征量检验出时间序列中是否含有非线性成分;并且采用样本熵的替代数据法比采用近似熵的替代数据法计算效率得到明显提高。所以,本研究得到结论:基于样本熵的替代数据法是一种准确、高效的非线性检测方法。当然本研究还需要进一步在其它数据上进行验证,来支持论文的结论。但是本文的结论对于时间序列的非线性检测,以及非线性动力学在时间序列分析中的应用,特别是越来越多的生理信号的分析,有着较大的价值。
[1]Jouny C C,Bergey G K.Characterization of early partial seizure onset:Frequency,complexity and entropy [J].Clinical Neurophysiology,2012,123 (4):658-669.
[2]Chen Z,Brown E N,Barbieri R.Characterizing nonlinear heartbeat dynamics within a point process framework [J].IEEE Transactions on Biomedical Engineering,2010,57(6):1335-1347.
[3]Faes L,Zhao H,Chon K H,et al.Time-varying surrogate data to assess nonlinearity in nonstationary time series:Application to heart rate variability [J].IEEE Transactions on Biomedical Engineering,2009,56 (3):685-695.
[4]Suzuki T,Ikeguchi T,Suzuki M.Algorithms for generating surrogate data for sparsely quantized time series [J].Physica D:Nonlinear Phenomena,2007,231 (2):108-115.
[5]Keylock C J.A wavelet-based method for surrogate data generation [J].Physica D:Nonlinear Phenomena,2007,225(2):219-228.
[6]Lucio JH,Valdes R,Rodriguez LR.Improvements to surrogate data methods for nonstationary times series [J].Physica Review E,2012,85 (5):056202.
[7]Spasi c'S.Surrogate data test for nonlinearity of the rat cerebellar electrocorticogram in the model of brain injury [J].Signal Processing,2010,90 (12):3015-3025.
[8]Suzuki T,Ikeguchi T,Suzuki M.Algorithms for gene-rating surrogate data for sparsely quantized time series [J].Physica D:Nonlinear Phenomena,2007,231 (2):108-115.
[9]Keylock C J.A wavelet-based method for surrogate data generation [J].Physica D:Nonlinear Phenomena,2007,225(2):219-228.
[10]Spasic Sladana.Surrogate data test for nonlinearity of the rat cerebellar electrocorticogram in the model of brain injury [J].Signal Processing,2010,90 (12):3015-3025.
[11]HUANG Xiaona,ZHANG Junying.The nonlinear analysis of epilepsy EEG signals[J].Editorial Department of Hexi University,2010,26 (2):49-52 (in Chinese).[黄小娜,张军英.癫痫脑电信号的非线性分析方法 [J].河西学院学报,2010,26 (2):29-32.]
[12]WANG Liyuan.The pathological fetal heart rate signal analysis used surrogate data [J].Journal of Changchun Normal University,2007,26 (2):49-52 (in Chinese). [王立媛.病态胎儿心率信号的替代数据分析 [J].长春师范学院学报(自然科学报),2007,26 (2):49-52.]
[13]Sohn H,Kim I,Lee W,et al.Linear and non-linear EEG analysis of adolescents with attention-deficit/hyperactivity disorder during a cognitive task [J].Clinical Neurophysiology,2010,121 (11):1863-1870.
[14]Ocak H.Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy[J].Expert Systems with Applications,2009,36 (2):2027-2036.
[15]Sohn H,Kim I,Lee W,et al.Linear and non-linear EEG analysis of adolescents with attention-deficit/hyperactivity disorder during a cognitive task [J].Clinical Neurophysiology,2010,121 (11):1863-1870.
[16]Lodha N,Naik S K,Coombes S A,et al.Force control and degree of motor impairments in chronic stroke [J].Clinical Neurophysiology,2010,121 (11):1952-1961.
[17]YU Qing.The analysis of correlation dimension calculation[J].Journal of Tianjin University of Technology,2004,20(4):60-62 (in Chinese).[于青.关联维数计算的分析研究[J].天津理工学院学报,2004,20 (4):60-62.]
[18]Cao Rui,Li Li,Chen Junjie.Comparative study of approximate entropy and sample entropy in EEG data analysis[J].BioTechnology:An Indian Journal,2013,7(11):493-498.
[19]Moorman J R,Delos J B,Flower A A,et al.Cardiovascular oscillations at the bedside:Early diagnosis of neonatal sepsis using heart rate characteristics monitoring [J].Physiological Measurement,2011,32 (11):1821-1832.
