基于全局敏感性分析方法的WASP模型不确定性分析

张质明,王晓燕,李明涛 (1.北京建筑大学北京应对气候变化和人才培养基地,北京 100044；.首都师范大学资源环境与旅游学院,北京 100048)

基于全局敏感性分析方法的WASP模型不确定性分析

张质明1,2,王晓燕2*,李明涛2(1.北京建筑大学北京应对气候变化和人才培养基地,北京 100044；2.首都师范大学资源环境与旅游学院,北京 100048)

为了定量讨论WASP(The water quality analysis simulation program,水质分析模拟程序)模型中各参数对模拟结果的影响及其不确定性,本文在Simulink环境下对模型进行重组,利用Sobol方法,对影响DO、CBOD、NH3-N、NO3--N等4项输出的各参数敏感性进行了研究,重点讨论了输入条件如时空变化对参数敏感性的影响.结果表明:Sobol全局敏感性分析方法能够有效地筛选出 WASP模型中对 DO、CBOD、NH3-N、NO变化模拟较为敏感的参数,在实现模型参数“本土化”中具有较大的应用潜力;对比总敏感性与一阶敏感性指数之间的差异, WASP模型当中的若干参数(如GP1、PNH3、anc等)耦合性较强,不宜使用一次一个变量法对这些变量进行敏感性分析;在参数敏感性变化方面,即使对于同一条河流,WASP的参数敏感性指数会因边界条件的时空变化而发生改变.敏感性受空间变化的影响不大,但受时间(季节)变化的影响显著;输入变量随时间的变化,会引起模型不确定性在各季节上的较大的差异;WASP模型当中存在明显的“异参同效”作用,仅靠传统方法进行全局寻优率定,并不能体现水体各组分之间相互转化的过程,还需要结合实验对关键参数进行率定.

不确定性分析；敏感性；Sobol方法；WASP模型；边界条件

水质模型中的不确定性研究已经成为当前水质模拟领域中的重要问题[1-7].由于在水质模型的应用中,众多的可调参数会造成一定的不确定性,特别是当“异参同效”[8-10]现象出现时,多种参数组合令模型结果均可满足模型的最优条件,无法通过水质模型准确解析实际中的污染物迁移转化规律.

为识别造成不确定性的主要参数[11-12],需要进行敏感性分析[13-14],方法主要分为局部敏感性分析与全局敏感性分析两种[15-16].局部敏感性分析的优势在于计算量小[17],但由于该方法建立在模型输出与参数的一阶偏导数关系上,对参数取值邻域的可导性提出了要求.为了能够更为准确的评估参数敏感性,现在更多的研究倾向于使用全局敏感性分析方法.目前常见的全局敏感性分析方法包括定性的Morris法、FAST法、GLUE法以及定量的Extend FAST法、Sobol法、基于ANN的权值分析法等[18].其中Sobol方法基于方差分解的原理,可用于非线性、非单调的数学模型、结果稳健可靠、并且能够给出对参数敏感性的定量评价,已经广泛应用于环境及其他领域大型非线性模型中[19-23].

目前针对参数对最终结果的所造成的影响方面的研究较多,而对模型内部各个子模块所描述的污染物转化过程所具有的不确定性方面的研究并不多见,且关于参数敏感性随时空条件变化会发生什么样的改变的研究并不多.为讨论WASP水质模型在不同时空条件下的重点参数及其所引起的不确定性,本文以北运河通州段为例,利用聚类分析方法确定出河道污染特征,作为空间上的划分依据;按照春、夏、秋、冬四季作为时间上的划分依据,分别对 DO、CBOD、氨氮、硝态氮等 4个方面的模拟进行敏感性分析,基于Sobol法识别出各条件下的重要敏感参数,用来研究不同输入条件下模型参数的敏感性变化.之后对WASP的分解模型使用蒙特卡罗模拟,确认参数不确定性对模型中各个模块所造成影响的大小,获取模型中的敏感模块.旨在为WASP模型的进一步优化、减少不确定性方面提供理论依据.

1 数据与方法

1.1 分析方法

1.1.1 Sobol方法 Sobol方法是基于方差分解的思想对敏感性进行评估的[24]:

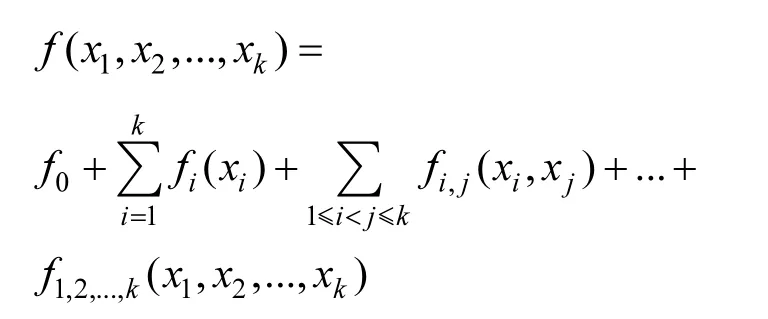
Sobol证明过分解式的唯一性并且所有分解项均可以通过多重积分求得[25]总方差为

偏方差可以通过分解式计算得到

敏感度系数1,2,...,sii iS 为

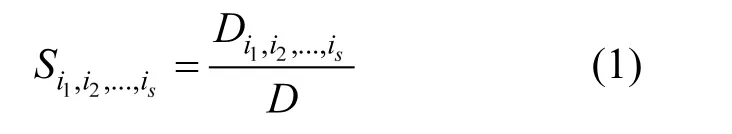
Si为 xi的一阶敏感性指数,用于定量描述 xi在函数f(x)中所造成的影响;叫做因素的s阶敏感性指数,用于定量描述这s个参数共同作用对函数 f(x)的影响.因此对于一个 s个参数的模型来说,变量总敏感性指数可以表示为:

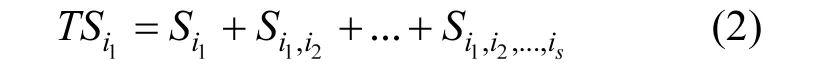
1.1.2 敏感性度量目标函数 目前关于模型参数敏感性度量主要从两个方面入手:一种是观察参数变化对模型输出值大小的直接影响,另外一种是通过参数变化对似然函数值造成的影响[26].本研究分别采用这 2种方法进行计算,似然函数使用平均相对误差以及Nash-Suttcliffe系数来衡量模拟值与观测值之间的拟合度,纳什系数表达式为:

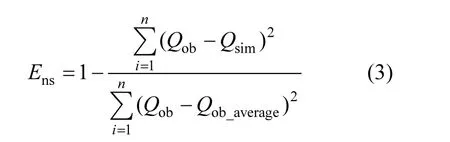
式中:Qob为观测值,Qsim为模拟值,Qob_average为观测平均值,n为观测的次数.当 Qob=Qsim时,Ens=1;若Ens＜0,则说明模型模拟无效.

1.1.3 模型的结构分解及参数 Simulink是MATLAB的可视化仿真工具,它基于 MATLAB的框图设计环境,可用于实现动态系统建模、仿真与分析.由于WASP在5.0之后的版本不再提供源码,为便于对模型的敏感性分析与参数率定,将 WASP6.0模型按照模型手册中的内容基于MATLAB/Simulink环境进行了重写.将 DO、CBOD、氨氮、硝氮的各个子过程(如:与 CBOD有关的氧化、死亡、反硝化、沉淀等作用机理)分别写入各自的m-function并定义其输出变量,最终集成在.mdl文件内.在本研究中,通过蒙特卡罗模拟方法,循环利用MATLAB中的sim命令调用该模型,获取自定义的输出变量获取各子过程的模拟结果,确定模型及其各子模块的输出范围,用于对模型的不确定性来源进行分析.

建模所涉及的机理过程、模型参数如表 1所示:

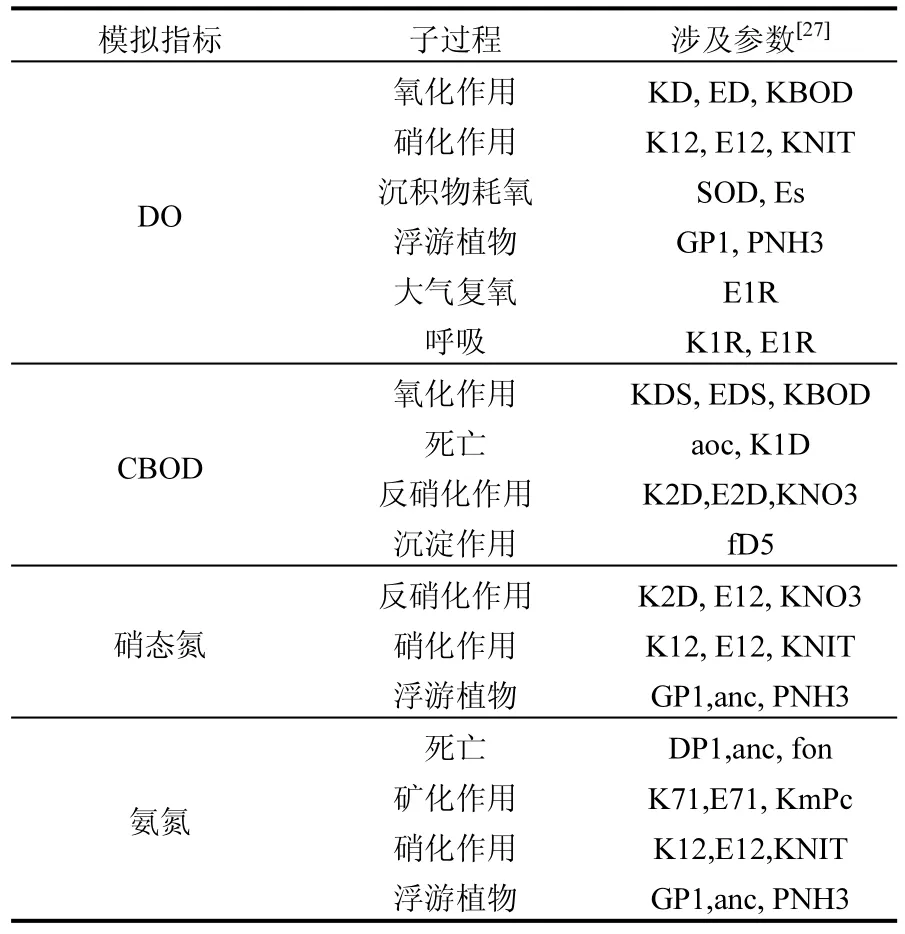
表1 模型所涉及的机理过程与参数Table 1 Mechanism processes and parameters referred to in the simulation of the four indicators

WASP应用的范围很广,很多河流都有WASP研究的案例,参数的选取范围也各不相同.特别是对于水动力条件受闸坝人为干扰明显的河流,参数的取值范围可能会与一般河流不同:例如水闸截流时的情形,参数范围就应当变化,甚至选取一些适用于湖泊水体的参数作为参考.因此本文模型参数的范围参照各类水体中的研究案例[27-31].

1.2 研究区域与数据来源

研究区北运河为唯一发源于北京境内的水系,闸坝多,流速缓慢,天然水量较少,多来自污水处理厂处理排放的再生水.课题组在 2009年4～10月以及2010年的4月、7月10月、12月对北运河通州段干流附近的共计14个样点的流量、流速以及水质(包括COD、CBOD、氨氮、硝态氮、DO、水温等指标)进行了同步采样监测.其中采样点布设及河段概化示意如图1所示.

图1 采样点空间分布与河道概化Fig.1 Location of monitoring sites of North Canal in Tongzhou

如图 1所示,监测点的重要排污口以及汇入的支流均加设置了监测点.根据监测数据,北运河通州段总磷浓度平均为0.70mg/L,超过地表水V类水标准[32].COD浓度为16.14～79.00mg/L,平均浓度为45.38mg/L,超过了地表水V类水标准.氨氮浓度为 1.88～25.80mg/L,占总氮的 78.0%,是北运河氮污染的主要指标.

2 结果与讨论

2.1 水质时空分布特征分析

普遍认为,水质变化的速率与水温、水力条件、水质状况等因素有很大的关系.在 WASP模型中,水质的变化速率的计算完全取决于这些状态变量以及相关常值参数.在模型计算过程中,状态变量取值差异,将会导致相关参数敏感性的差异.

在主要的状态变量中,水温主要受到季节因素的影响;水力条件主要受到水系汇流状况、季节因素以及闸坝控制的影响;河道水质状况(包括 DO、COD、氨氮、BOD、总磷等指标)除了受到季节因素的影响[33]以外,还与河段流经区域的土地利用有关[34-36],因此状态变量的变异可以分解为时间、空间两方面分别进行讨论.

为了研究水质污染状况随空间变化是否引起模型参数敏感性的变化,本研究采用聚类分析法来识别北运河不同河段的污染物组成特征.根据对监测水质、流量数据的相关性分析,发现在诸多的状态变量中存在一定的相关性.为了避免重复考虑这些因素,筛选出相对较为独立的DO、氨氮、COD等3个指标归一化后进行聚类分析,结果如图2所示.

图2 采样点聚类分析结果Fig.2 Dendrogram showing clustering of sampling sites of the North Canal

如图2所示,除8号采样点以外,其余采样点监测到的水质特征随与空间的变化而变.采样点1与采样点2为代表的人口密集的居住区纳污河段(类型 I),工业污染源较少,主要污染物来源为集中处理设施;3、4、5、6、7代表城乡结合部的水质特征(类型II),9、10、11、12、13、14代表流经农业用地、林地等人口较稀疏区域的河段(类型 III),主要污染来自面源.由于水温随季节变化明显,且作为重要变量参与WASP模型中的多个模块的计算,因此温度水平按季节进行划分.由于北运河水量受闸坝影响明显,因此为保证流量的典型性,选用置信水平为 90%的监测值来代表其正常范围.根据此3类河段的各指标监测范围,确定模型输入变量的上下界,其中受到季节性影响较大的温度及流量数据范围见表2.

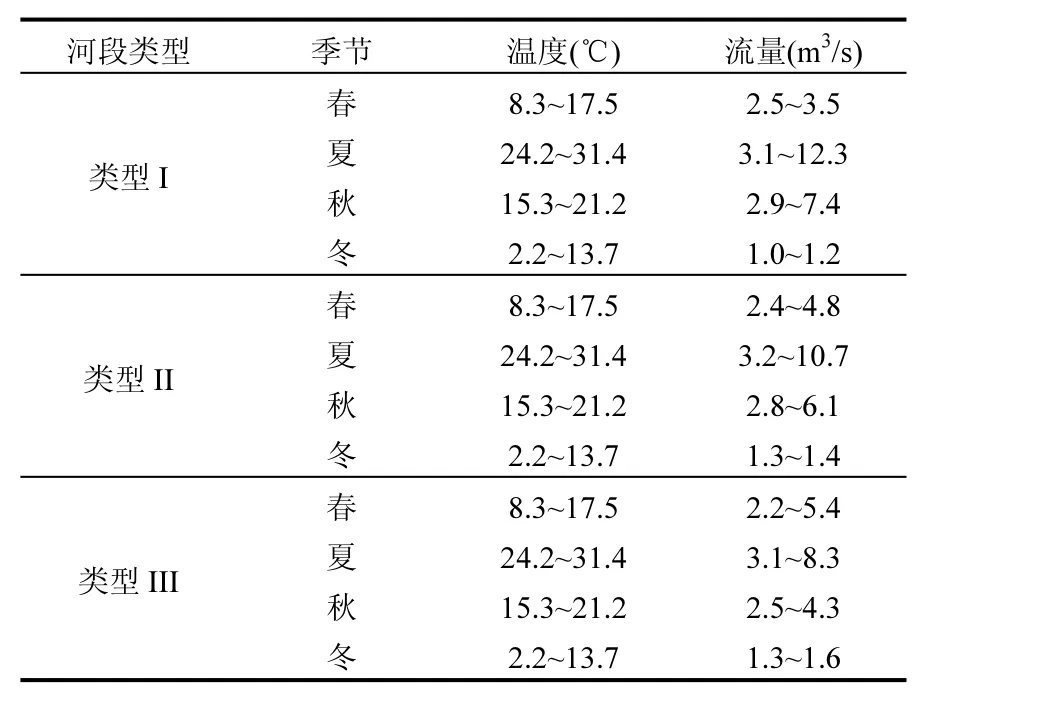
表2 研究区域季节性指标数据范围Table 2 Range of the seasonal indexes

2.2 模型不确定性分析

本研究将模型的不确定性分为整体与子模块两方面来进行讨论.模型的整体输出不确定性主要体现参数变化给模型输出指标带来的影响;子模型的不确定性可以体现整体输出不确定性在各子模块的分量.

2.2.1 模型整体输出的不确定性 蒙特卡罗模拟中,模型参数可根据实际数据所展现的特征为依据来确定服从何种分布,但对于无法进行参数界定概率分布的时候,一般情况可假设为均匀分布[37].本研究将这些参数设定为均匀分布.模拟所形成的条带状轨迹如图 5所示.其中CBOD、NH3-N、NON等指标拟合趋势较好,而 DO 拟合效果不佳,这可能与模型输入数据步长有关,由于DO在一天之内的变化幅度也较其他指标大,以步长单位为 1d的输入数据无法满足其模拟精度.

图3 2009年4月～2010年12月该河段内年蒙特卡罗模拟下的模型的整体输出Fig.3 Monte Carol simulation of the different indicators of WASP from April, 2009to December, 2010at Yulin Zhuang Segment观测值为除枯水期以外的月监测数据

以受闸坝干扰较小的榆林庄桥断面为例,DO的模拟中,秋、冬的不确定性小于春、夏两季;CBOD模拟中,夏季的不确定性最低;NON的模拟中冬季不确定性最低,其余季节不确定性相差不大;NH3-N模拟的不确定性四季相差不多.可见,对于同一个参数范围,由于输入条件的随时间的变化,参数对模型所造成的不确定性也可能随变量水平的不同有着较大差异.

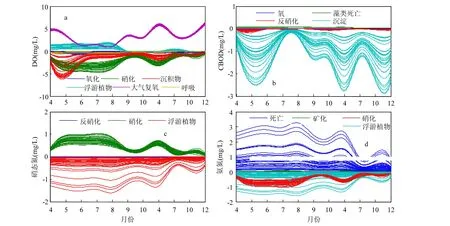
图4 蒙特卡罗模拟下的模型的各子模块的输出Fig.4 Sub-models’ respond under Monte Carol simulation of WASP

2.2.2 子模块不确定性 由于WASP模型的最终输出是由若干个子模块共同决定的,其中DO的模拟包括因水中CBOD的氧化所消耗的DO、藻类呼吸所消耗的 DO、因氨氮的硝化作用所消耗的DO、沉积物氧化分解所消耗的 DO、浮游植物生长过程中因光合作用产生的DO、大气复氧所增加的DO;CBOD的模拟包括CBOD氧化所消耗的量、反硝化菌因消耗碳源所减少的 CBOD、因沉淀作用所减少的CBOD、藻类死亡所产生的CBOD;硝态氮的模拟包括因反硝化作用所减少的硝态氮、浮游植物生长所消耗的硝态氮,因氨氮硝化所增加的硝态氮;氨氮的模拟包括因矿化作用所减少的氨氮、因硝化作用所减少的氨氮、浮游植物生长所消耗的氨氮、藻类死亡所产生的氨氮.根据蒙特卡罗模拟的结果,各个模块的不确定性如图4所示.

可以看出,对于DO的模拟,不确定性主要来自于沉积物、硝化作用等子模块;CBOD的模拟方面,不确定性主要来自于沉淀作用;NO3-N模拟方面,不确定性主要是硝化作用与浮游植物生长; NH3-N的模拟方面,不确定性主要来自于浮游植物的死亡、生长及硝化作用.然而,尽管NO3-N、NH3-N的模拟方面均有多个模块存在较大的不确定性,但是最终叠加的结果的不确定性却并不大.这说明WASP模型当中存在明显的“异参同效”作用,各个子模块此消彼长,仅靠传统方法进行全局寻优率定,并不能体现水体各组分之间相互转化的过程,还需要结合其他手段对关键参数进行率定.

另外,由图4可以看出,同一个子模块,在不同的时期的不确定性也会发生很大的变化,这是由于输入条件的改变所造成的.

2.3 模型参数敏感性分析

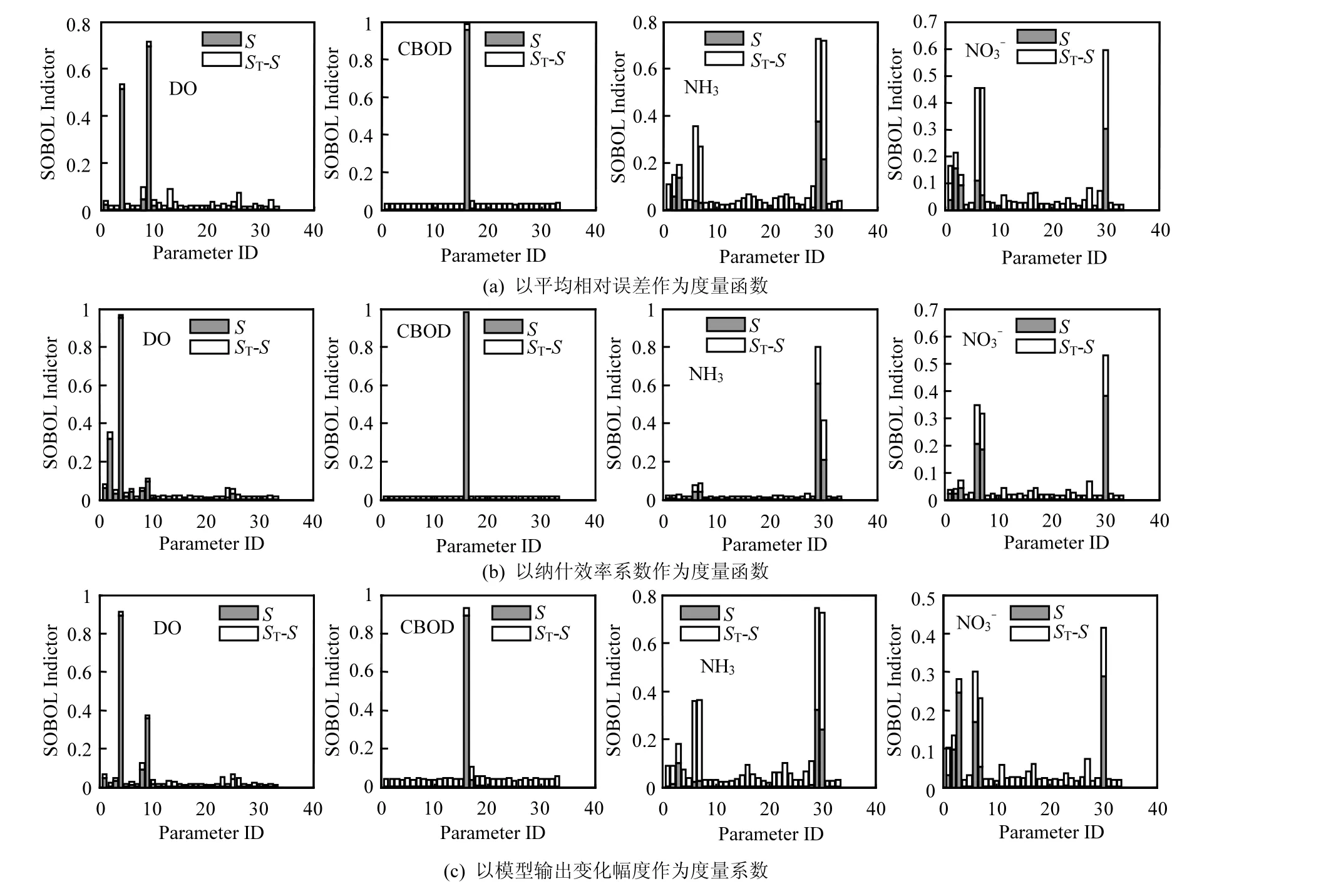
图5 各指标模拟参数敏感性指数Fig.5 Sobol’s index of the parameters in the simulation of each indicatorS为一阶敏感性指数,ST为总敏感性指数,ST-S即为由参数之间交互、协同作用产生的影响

2.3.1 WASP模型主要敏感参数的确定 基于Sobol方法,利用输出变化量以及纳什系数(NSE)、平均相对误差(MSE)两个统计量作为似然函数进行敏感性的度量.结果如图5所示.

图 5展示了以不同度量方法所得到参数总敏感性指数与一阶敏感性指数.总体上来讲 3种方法结果具有一致性.这是因为对于模型输出有着显著影响的参数,其对模型的精度所产生的影响也相对较大.但是在进行似然函数计算时,各个参数相当于在模型计算的基础上又进行了一次函数作用,因此参数相互之间的耦合作用就会进一步增强.如图2所示,当对于敏感性的度量选用似然函数时,参数总敏感性一般要比一阶敏感性大得多;而选用模型输出变化幅度时,参数的总敏感性与一阶敏感性之间的差异较小.这就说明,尽可能选用形式较为简单似然函数,有助于在研究参数敏感性问题中,减少因人为在使用似然函数时所造成的干扰.

综合以上结果,得到WASP模型中对结果产生主要作用的参数(表3).

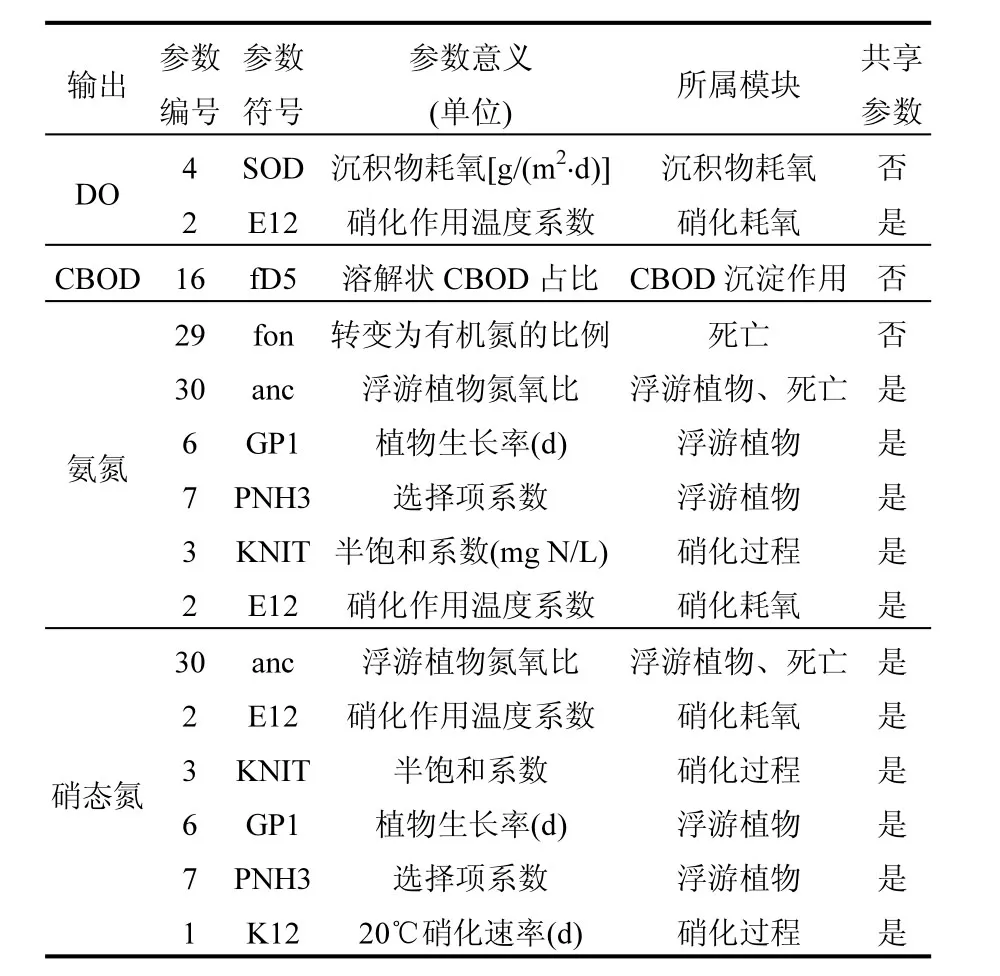
表3 WASP模型主要参数Table 3 The main sensitive parameters of WASP simulation at Tongzhou part of the North Canal

由表3可见,除SOD、fD5、fon外,其他对最终结果产生重要影响的参数,均参与多个模块计算.尽管这些参数在各个模块中的重要性不一致,但仍可能会与其他参数产生较强相互作用,如参数6、7、30,都在其相应的模块中出现了总敏感性指数远大于一阶敏感性指数的现象.由于这类参数敏感性会因其他参数的取值不同而发生较大的变化.通过一次变化一个参数而固定其他参数进行的局部敏感性分析就无法得到准确的结果.因此“一次一个变量”的敏感性评估方法对于这类参数来说并不适用.

对比利用蒙特卡罗模拟结果可以看出,敏感参数的所属子模块,其不确定性也较高:DO模块中,参数SOD决定着沉积物耗氧量, E12决定着硝化作用的强弱,在DO的模拟中,这两个参数的取值非常关键;CBOD模块中,参数fD5能够很大程度地决定模拟过程中沉淀量的多少,是模拟CBOD浓度的关键;硝态氮中的多个敏感参数也都集中在浮游植物生长与硝化过程的子模块中;氨氮模拟中的敏感参数也均集中在浮游植物的生长、死亡、硝化过程等子模块中.

但是由于边界条件的改变会造成参数敏感性也随之发生变化,所以尽管敏感参数在整个的模拟过程中呈主导地位,但在一定条件下的特殊时期,可能会发生变化.

2.3.2 输入条件变化对参数敏感性的影响 为讨论季节变化与空间变化所引起输入条件的改变对参数敏感性的影响,本研究以四季的水质水量均值数据作为模型的输入数据,用于体现四季的变化;以空间聚类分析结果的各类区域均值作为模型输入,用于体现空间变化.

(1) 季节变化对参数敏感性的影响:我国北方城市的河流季节性较强,往往在不同的季节水量不同,并同时呈现不同的水质特征.季节影响着输入变量的同时,也会影响参数在一定时间范围内所呈现的敏感性.以榆林庄桥断面的监测数据为例,通过对四季的数据变化,分别进行参数的敏感性计算,结果如图6所示.

由图 6可知,即使对于相同的河段来说,输入条件在季节上的变化也会引起同一个参数敏感性的显著改变.其中春、夏的敏感性分布情况较为接近,而秋、冬敏感性分布较为接近.这就意味着在参数率定方面,如果依照季节的不同,对参数进行有针对性的率定,可以显著改善率定工作的效率.

图6 不同季节条件下的各参数敏感性指数Fig.6 Sobol indices of the parameters in different seasons

对比图5与图6可以发现,在CBOD的模拟中,尽管参数 fD5(16号参数)在整体上是不确定性的主要来源(尤其是春、夏两季),但是在秋、冬两季的模拟中,其他参数对 CBOD的模拟影响程度有所加大.因此在确定该参数 fD5之后,在秋冬两季的模拟中继续对其他参数的率定,可以作为对该时间段模拟输出值的微调,以提高模拟精度.

区分各个时间段内影响水质模拟的主要参数,可以为改善局部的模拟效果提供一定得理论依据.图 3中所示,在该河段内,春、夏时段内的CBOD模拟,夏、秋、冬时段内的DO模拟,秋、冬时段内的NH3、NO3模拟都只有一个主要参数,通过率定相应的主要参数,就可以显著缩小模拟的不确定性.

(2) 空间变化对参数敏感性的影响 根据聚类分析得到的 3种不同类型的河段进行参数的敏感性计算(图7).

图7 不同区域类型条件下的各参数敏感性指数Fig.7 Sobol indicesof the parameters in different area of the North Canal

由图7可见,在水质特征不同的河段上,参数敏感性大小存在一些变化:其中变化最大的地方存在于NO3-N模拟中,参数E12、KNIT(2、3号参数)的敏感性在第3类区域中明显比其他两类区域要低,这是因为第3类区域当中NO3-N明显比其他两个区域的含量低所造成的.

但从整体上看,北运河通州段内的空间变化一般并不影响参数的主导地位.这有可能是由于北运河整体水质较差,虽然根据聚类分析能够依据水质特征区分出不同类型的河段,但各河段均属重污染、缺水型的纳污河流,对于这类水体的模拟来说,其参数的敏感性基本保持统一,也就是说在参数率定过程中,其率定的优先级随着空间的改变不会发生变化.

3 结论

3.1 对比总敏感性与一阶敏感性指数之间的差异,发现WASP模型当中的若干参数耦合性较强,不宜使用一次一个变量法对这些变量进行敏感性分析.

3.2 WASP的参数敏感性指数会随模拟对象的时、空变化而发生改变;其中时间(季节)变化的影响甚至可能会导致敏感参数数量上的变化,而空间变化的影响力不大.

3.3 WASP模型的不确定性在各个季节上也有一定差异:DO的模拟中,秋、冬的不确定性小于春、夏两季;CBOD模拟中,夏季的不确定性最低;NON的模拟中冬季不确定性最低,其余季节不确定性相差不大;NH3-N模拟的不确定性四季相差不多.

3.4 WASP模型当中存在明显的“异参同效”作用,各个子模块此消彼长,仅靠传统方法进行全局寻优率定,并不能体现水体各组分之间相互转化的过程,还需要结合实验对关键参数进行率定.3.5 对于在一定时空条件下敏感性会突增的参数,应当在该条件下另行率定.

[1] Vivian P, Roberto J C. Qual2E model for the Corumbata´ı River[J]. Ecological Modelling, 2006,198:269—275.

[2] Mehmet Y, Erdal K, Ridvan B. Simulation of river streams:Comparison of a new technique with QUAL2E [J]. Mathematical and Computer Modelling, 2007,46:292—305.

[3] Fan C H, Ko C H, Wang W S. An innovative modeling approach using Qual2K and HEC-RAS integration to assess the impact of tidal effect on River Water quality simulation [J]. Journal of Environmental Management, 2009,90:1824—1832.

[4] Lin C E, Chen C T, Kao C M, et al. Development of the sediment and water quality management strategies for the Salt-water River,Taiwan [J]. Marine Pollution Bulletin, 2011,63:528—534.

[5] Thorsen M, Refsgaard J C, Hansen S, et al. Assessment of uncertainty in simulation of nitrate leaching to aquifers at catchment scale [J]. Journal of Hydrology, 2001,242:210-227.

[6] Karl-Erich L, Katrin F, Martina B. Structural uncertainty in a river water quality modeling system [J]. Ecological Modelling,2007,204:289—300.

[7] Fabrizio B, Benedicte L, Eva L G, et al. Estimation of sampling uncertainty in lake-water monitoringin a collaborative field trial[J]. Trends in Analytical Chemistry, 2012,36:176-184.

[8] Keith B, Jim F. Equinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology [J]. Journal of Hydrology,2001,249:11-29.

[9] Reichert P, Omlin M. On the usefulness of over parameterized ecological models [J]. Ecological Modelling, 1997,95:289-299.

[10] Lindenschmidt K E. The effect of complexity on parameter sensitivity and model uncertainty in river water quality modeling[J]. Ecological Modelling, 2006,190:72-86.

[11] 王建平,程声通,贾海峰.基于MCMC法的水质模型参数不确定性研究 [J]. 环境科学, 2006,27(1):24-30.

[12] Lindim C, Pinho J L, Vieira J M P. Analysis of spatial and temporal patterns in a large reservoir using water quality and hydrodynamic modeling [J]. Ecological Modelling, 2011,222:2485-2494.

[13] Cea L, Bermúdez M, Puertas J. Uncertainty and sensitivity analysis of a depth-averaged water quality model [J].Environmental Modelling and Software, 2011,26:1526-1539.

[14] Saltelli A, Annonis P. How to avoid a perfunctory sensitivity analysis [J]. Environmental Modelling and Software, 2010,25:1508-1517.

[15] Saltelli A, Tarantola S, Chan K P S. A quantitative model independent method for global sensitivity analysis of model output [J]. Technometrics, 1999,41(1):39-56.

[16] 张 巍,郑 一,王学军.水环境非点源污染的不确定性及分析方法 [J]. 农业环境科学学报, 2008,27(4):1290-1296.

[17] Griensven A, Meixner T, Grunwald S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models [J]. Journal of Hydrology, 2006,324:10-23.

[18] 蔡 毅,邢 岩,胡 丹.敏感性分析综述 [J]. 北京师范大学学报(自然科学版), 2008,44(1):9-16.

[19] Sobol' I M. Sensitivity estimates for non-linear mathematical models [J]. Mathematical Modelling and Computational Experiment, 1993,4(1):407-414.

[20] Florian P, Keith B, Marco R, et al. Multi-method global sensitivity analysis of flood inundation models [J]. Advances in Water Resources , 2008,31:1-14.

[21] Dimov I, Georgieva R, IvansovskaS, et al. Studying the sensitivity of pollutants’ concentrations caused by variations of chemical rates [J]. Journal of Computational and Applied Mathematics, 2010,235:391-402.

[22] Yang J. Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis [J]. Environmetal Modelling and Software, 2011,26:444-457.

[23] Thierry A Mar, Stefano T. Variance-based sensitivity indices for models with dependent inputs [J]. Reliability Engineering and System Safety, 2012,107:115—121.

[24] Nossent J P Elsen. Sobol’ sensitivity analysis of a complex environmental model [J]. Environmental Modelling and Software,2011,26(12):1515-1525.

[25] 李 睿.Sobol灵敏度分析方法在结构动态特性分析中的应用研究 [D]. 长沙:湖南大学, 2003.

[26] 王纲胜,夏 军,陈军锋.模型多参数灵敏度与不确定性分析 [J].地理研究, 2010,29(2):263-270.

[27] Tim A Wool, Robert B Ambrose, James L Martin, et al. Water quality analysis simulation program (WASP) Draft: User’s manual [M]. Atlanta: US Environmental Protection Agency, MS.Tetre. Tech., 2001.

[28] 王旭东,刘素玲,张树深,等.白洋淀水域 WASP富营养化模型改进研究 [J]. 环境科学与技术, 2009,32(10):19-24.

[29] Arhonditsis G B, Brett M T. Eutrophication model for Lake Washington (USA) Part I. Model description and sensitivity analysis [J]. Ecological Modelling, 2005,187:140-178.

[30] 路成刚.基于WASP7.3的南四湖水质模拟分析研究 [D]. 青岛:青岛理工大学, 2010.

[31] 史铁锤,王飞儿,方晓波.基于 WASP的湖州市环太湖河网区水质管理模式 [J]. 环境科学学报, 2010,30(3):631-640.

[32] 于 洋.北运河水体中氨氮的氧化过程及微生物响应特征 [D].北京:首都师范大学, 2012.

[33] 方晓波,骆林平,李 松,等.钱塘江兰溪段地表水质季节变化特征及源解析 [J]. 环境科学学报, 2013,33(7):1980-1988.

[34] Whitehead P G. Steady state and dynamic modeling of nitrogen in the River Kennet: impacts of Land use change since the 1930s [J].The Science of the Total Environment, 2002,282:417-434.

[35] Vaze J, FrancisH S Chiew. Experimental study of pollutant accumulation on an urban road surface [J]. Urban Water,2002,4:379-389.

[36] 孙金华,曹晓峰,黄 艺.滇池流域土地利用对入湖河流水质的影响 [J]. 中国环境科学, 2011,31(12):2052-2057.

[37] 邹 锐,朱 翔,贺 彬,等.基于非线性响应函数和蒙特卡洛模拟的滇池流域污染负荷削减情景分析 [J]. 环境科学学报,2011,31(10):2312-2318.

Uncertainty analysis of WASP based on global sensitivity analysis method.

ZHANG Zhi-ming1,2, WANG Xiao-yan2*,LI Ming-tao2
(1.Beijing Climate Change Response Research and Education Center, Beijing University of Civil Engineering and Architecture, Beijing 100044, China；2.College of Resources, Environment and Tourism, Capital Normal University, Beijing 100048, China). China Environmental Science, 2014,34(5)：1336～1346

To quantitatively evaluate parameters influence and uncertainty of model, WASP model was reorganized by Simulink in this paper. Sensitivity of the parameters related to model output of DO, CBOD, NH3-N and NO3--N was studied based on Sobol method. In particular, sensitivity changes with temporal and spatial variations of input were discussed. Global sensitivity analysis of Sobol method can identify the most sensitive parameters of the process simulation; The significant difference between the total sensitivity and first-order sensitivity index showed that some parameters (e.g. GP1, PNH3, anc, etc.) of the WASP model were strongly coupling, and“One variable at a time”method was inappropriate to evaluate the sensitivity of these parameters; Sensitivity index of WASP parameter changed with the temporal and spatial variation of boundary conditions, even for the same river; WASP model showed an obvious equifinality for different parameters, so the traditional methods such as the global optimization calibration, failed to simulate the mechanism process. Experiments were required as a verification for calibration of key parameters.

uncertainty analysis；sensitivity；Sobol method；WASP model；boundary conditions

X703

A

1000-6923(2014)05-1336-11

2013-09-10

国家自然科学基金项目(40971258,41271495);高等学校博士学科点专项科研基金联合资助项目(20121108110006);北京市教委北京市应对气候变化研究基地(2014年)(市级)专项(PXM2014_014210_000037)

* 责任作者, 教授, cxnwxy@sohu.com

张质明(1984-),男,北京人,博士,主要从事水质模拟、模型不确定性方面的研究.发表论文10余篇.