最小生成树在城市地下管网优化中的应用

朱恒其 张 颖 王华雨

（泰州职业技术学院，江苏 泰州225300）

由于城市化进程的进一步加快，人口的快速增长，城市对电力电缆、通信电缆、给水排水管线、燃气管理等维持城市“生命力”的各种市政管线的需求量日益剧增。 因此，各管线承建单位为了满足发展现状或未来的需求，需要挖掘城市道路来铺设、更新和维修管线，经常刚铺好的道路，很快会被其它管理单位开挖施工，如此反复，让人恨不得在马路上安条“拉链”。

为解决这样的问题，我市市政出台了若干新规，并开始了地下管廊的建设研究工作。 地下管廊一般设置在地下，将各类公用管线集中容纳于一体，并留有供检修人员行走通道的隧道。 地下管廊设有专门的检修口、吊装口和监测系统，实施统一规划、设计、建设和管理，彻底改变以往各自建设、各自管理的零乱局面。 而且避免了酸碱物质的腐蚀，延长了管线的使用寿命。 但地下管廊的开发初期需要投入的费用较大,为缓解财政压力,可以利用图论理论求出城区主干线的最小生成树，使总修建长度之和最小。

1 图论模型的建立

设赋权连通无向图G(V,E)是城市道路构成的网络图，其中，V 表示图中所有的顶点集(vi)，E 表示由城市道路构成的弧集，道路的长度用边权d(vivj)表示，如图1 所示。

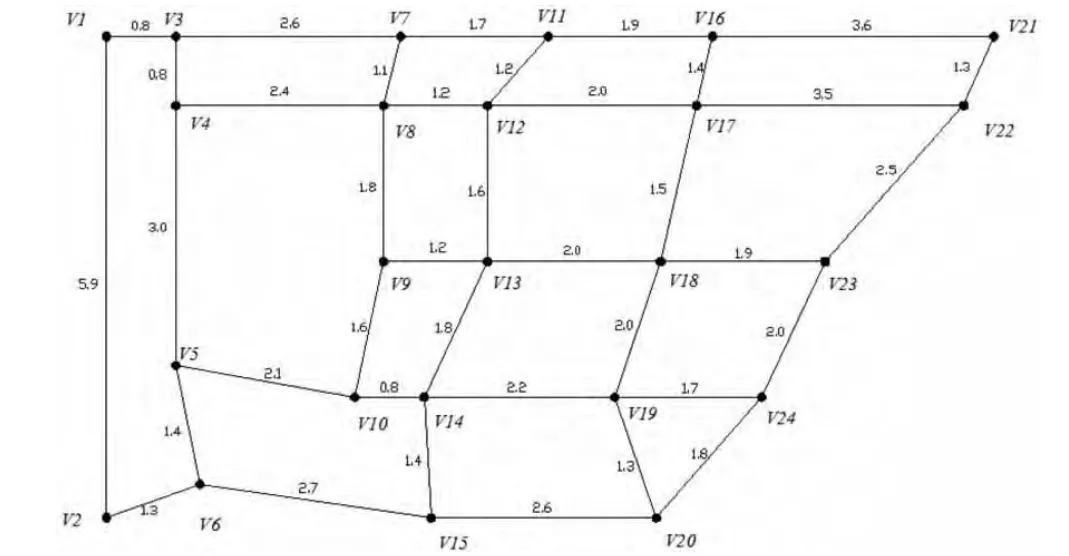
图1

2 模型的求解

求最小生成树的方法常用的算法主要有Prim 和Kruskal 算法，这里我们选用Prim 算法。

令P={vi},Q={}， 分别用于存放G 的最小生成树中的顶点和边。Prim 算法的的思想是：从所有p∈P，v∈V-P 的边中，选取具有最小权值的边pv，将顶点v 加入集合P 中，将边加入集合Q 中，如此不断重得，直到P=V，最小生成树构造完毕。 具体程序如下：

clc;clear;

a=zeros(24);

a(1,2)=5.9;a(1,3)=0.8;a(2,6)=1.3;……;a(23,24)=2;

a=a+a';a(find(a==0))=inf;

result=[];p=1;tb=2:length(a);

while length(result)～=length(a)-1

temp=a(p,tb);temp=temp(:);

d=min(temp);

[jb,kb]=find(a(p,tb)==d);

j=p(jb(1));k=tb(kb(1));

result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];

end

Result

程序运行后，即可求得最小生成树，如图2。

图2

3 模型评价

该模型结合实际给出了城市主干线上的最小生成树，为城市修建地下管廊提供方案。 若考虑不同道路适宜修建不同类型管廊，即不同道路的修建成本不同时，可通过改变相应的边权值，重新由Prim 算法得出最小生成树。

［1］郭培俊，毛海舟.高职数学建模[M].浙江：浙江大学出版社，2010，12.

［2］司守奎.数学建模算法与应用[M].国防工业出版社，2011，08.