基于赤迟信息准则的人因可靠性模型变量选择
2014-12-23魏文斌
魏文斌 万 劼
(首都经济贸易大学安全与环境工程学院,中国 北京 100070)
0 绪论
随着科技发展,设备自身的可靠性不断提高,人机系统的可靠性愈来愈取决于人的可靠性[1]。人因可靠性分析(HRA)主要研究人的失误对系统的风险所造成的影响。近年来,该领域研究取得很大进展。王遥、黄祥瑞等[2]通过模拟机实验给出了操纵员响应时间数据的处理方法。张力、黄曙东等[3]对核电站人员可靠性、复杂人-机系统人员可靠性等进行了研究。肖国清等[4]学者在对人的行为原理进行分析的基础上,讨论了3 种可靠性机理及其影响因素,应用模糊数学理论建立了可靠性评价模型。目前,各种HRA 方法仍存在着过多依赖专家判断、难以将对人误概率有显著影响的因子定量化的问题。由于人误因素复杂,故回归模型中回归元的个数过多,增加了回归分析的难度。本文先引入定性响应模型与虚拟变量回归,在此基础上利用赤迟信息准则,在不降低预测精度的前提下进行变量选择,给出一个解决上述问题的可行方法。
1 定性响应回归模型
1.1 线性概率模型
在突发状况下,应急人员进行处置的结果有两种,一是处置成功,二是处置失败,事故发生。令应急处置结果为变量Y,若处置成功取Y值1,否则取Y 值为0,这样Y 就是一个(0-1)变量。构造定性响应回归模型:

其中X1,X2,……,Xn为对因变量即应急处置结果有影响的情境因子,先假定其为定量变量。εi为随机干扰项,E(εi)=0。对方程(1.1.1)求条件期望可得:
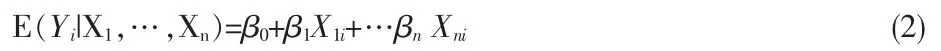
若突发状况下应急人员成功处置的概率为Pi,则应急处置失败的概率为1-Pi,则变量Yi服从参数为Pi的(0-1)分布,其期望值为Pi。根据上述讨论可知,若对应急处置数据拟合方程(1)将得到在给定情境下,应急人员成功处置突发状况的概率Pi。而偏回归系数βi则给出了在保持其余解释变量保持不变的条件下,回归元Xi每变化一个单位时,应急人员成功处置突发状况的概率Pi的变化量。
1.2 虚拟变量回归模型
实际上人因可靠性分析领域情境因子多为定性变量,如在认知可靠性及失误分析方法(CREAM)中将可能对人行为有影响的情境因素归结为一系列的共同绩效条件(CPC 因子)。为量化定性回归元的影响,可根据其水平数k,构造(k-1)个取值为0 或1 的虚拟变量,1 代表回归元取此水平,0 代表不取此水平。若突发状况应急处置的结果Yi仅受CPC 因子“培训和经验的充分性”的影响,由于该因子具有三个水平“充分,经验丰富”、“充分,经验有限”、“不充分”[5],分别记为E1、E2、E3。可设虚拟变量的回归方程为:

拟合数据得到其样本回归函数:

对上述回归方程可做如下解释:在假定应急处置结果仅受“培训和经验的充分性”一个CPC 因子影响时,级差截距系数βˆ0给出在该因子处于“充分,经验丰富”水平时,应急处置人员成功处置突发状况的概率。而级差截距系数βˆ1、βˆ2则给出了当此CPC 因子处于另外两个水平时,“处突”成功概率与基准组的差距值。通过构造虚拟变量将其余CPC 因子引入模型,且对于每个CPC 因子所定义的虚拟变量的个数必须比该因子具有的水平数少1,以避免导致模型中回归元的完全共线性。模型中不显式存在的CPC 因子的水平为基准组,基准组对于应急处置成功概率的影响通过回归方程的截距项予以表达,所有其它水平对成功概率的影响都与基准组的概率相比较。
2 赤迟信息准则
2.1 AIC 统计量
根据上述讨论,可以在CREAM 法共同绩效条件指标体系的基础上构造虚拟变量,进而建立定性响应回归模型,分析变量间相关关系,以得到各CPC 因子水平对应急处置成功概率的定量影响。CREAM 有9 个CPC 因子,共29 个水平,因此需要构造20 个虚拟变量,变量过多,不利于预测,需要对变量进行选择。如果在回归方程中删去了对被解释变量Y 有显著影响的自变量,那么方程必然与实际产生较大偏离,但若在回归方程中包括所有可能变量,将导致方程过于臃肿,使用繁琐,且若方程中存在对因变量影响不显著的回归元,将使得残差平方和(RSS)增大进而增大误差。为增强回归方程的预测能力,可采用赤迟信息准则对方程中回归元进行选择。
赤迟信息准则(Akaike Information Criterion,AIC)是由日本统计学家赤迟弘次创立的一种衡量统计模型拟合优良性的标准,它建立在熵的基础上,用以衡量回归模型的复杂度及其拟合数据的优良性。AIC统计量如下方程所示[6]:

方程中RSS 为回归的残差平方和,n 是观测数,k 为方程中解释变量的个数。其中2k/n 被称为惩罚因子,与其它对拟合优度进行度量的统计量相比,AIC 对在回归方程中添加回归元施加了更为严厉的处罚[7],其目的是寻求能够最好拟合数据但包含最少回归元的方程。AIC统计量不仅能够描述回归方程对给定样本数据的拟合优度,还能够描述拟合模型在给定自变量值下对因变量未来值的预测,在从一组可供选择的模型中选取最佳模型时,AIC 值最小的模型是可取的[8]。
2.2 利用AIC 统计量进行变量选择
利用AIC 统计量进行变量选择的过程如下:
1)用全部可能对应急处置概率有影响的解释变量进行回归,计算回归后的AIC 值;
2)每次减去一个回归元,用剩余回归元进行回归并计算回归方程的AIC 值,依次计算去掉每一个回归元后方程的AIC 值后,将这一轮使得方程AIC 值下降最多的那个回归元真正从方程中排除;
3)重复此过程,直到方程的AIC 值达到最小,在此情况下无论再从方程中去掉哪一个回归元都将导致回归方程的AIC 值上升,这时便得到了“最优”回归方程。
3 实例应用
本文用上述方法分析挖掘机作业中突发状况下人的应急可靠性,在CREAM 法CPC 因子体系的基础上构造虚拟变量如表1 所示。
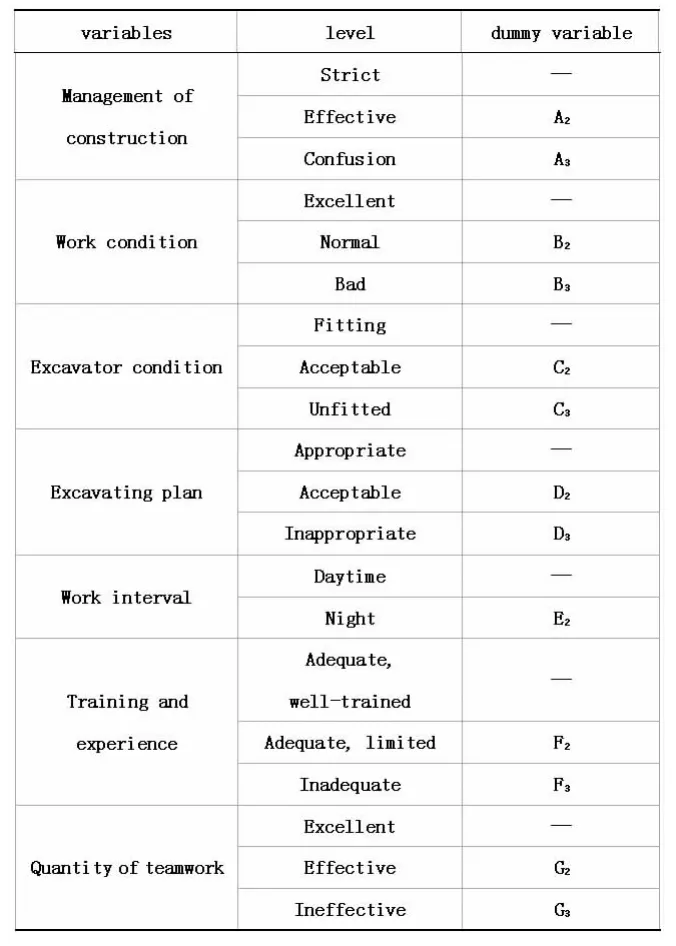
表1 虚拟变量设定
进入北京盛博为建筑装饰公司施工现场向工程建设方、施工方及建立方进行调研,得到该项目2014 年上半年挖掘机突发状况应急处置数据,数据包括了每次突发状况下挖掘机驾驶员进行应急处置时的状态信息,将数据以表1 所示的形式转化为各虚拟变量。对上述数据拟合定性响应模型,进行数据变换后,利用统计R 软件[9]进行基于赤迟准则的逐步回归,可得结果如表2、表3 所示的变量剔除结果。
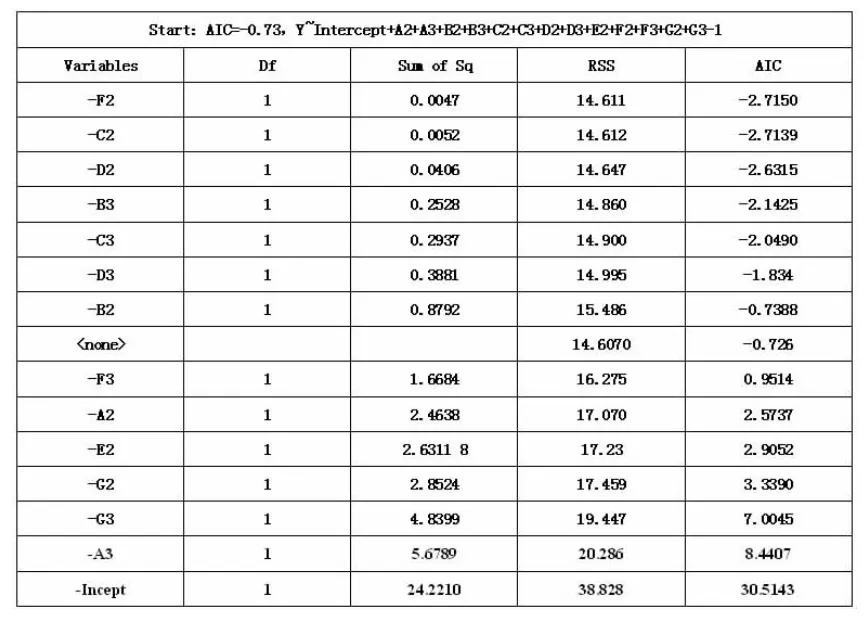
表2 变量剔除运算
经过7 轮计算后可得表3 结果。
从表3 中计算结果可知,经过7 轮计算剔除了7 个变量后,回归方程AIC 值已到达最小,在下一轮计算中无论去掉哪一个变量,AIC值均会升高,故变量剔除计算结束。经过剔除变量,得到了对突发状况下挖掘机驾驶员应急处置可靠概率有显著影响的6 个虚拟变量。
得到各个显著变量之后,可以用得到显著变量与待解释变量(应急处置结果)建立回归模型,以预测在突发状况下应急人员的响应可靠性。所用的回归模型可以是线性或非线性(如Logistic)的。另外,从以上的基于AIC 准则的变量显著性分析中,还可以得出以下结果:施工现场管理、班组合作质量、值班时间区间、培训和经验为影响应急处置结果的最为显著的几个因素。

表3 变量剔除最终结果
4 结论
本文讨论了利用赤迟信息准则对基于CPC 因子建立的虚拟变量回归模型进行了变量剔除的方法,有利于提高模型的预测准确度及解释能力,为HRA 领域建立人因可靠性模型提供了一些新的思路。并结合建筑工程领域挖掘机作业的HRA 予以说明,通过根据AIC 值进行变量剔除,得到对于突发状况下挖掘机驾驶员应急处置可靠概率有显著影响的虚拟变量为培训和经验不充分、施工现场管理很乱等6 个因素。因此本文认为:对于工程管理人员而言,在日常工作中,应该把施工现场管理、优化班组合作以及培训的加强放在最为突出的重要位置。
[1]张力,黄曙东,何爱武,杨洪.人因可靠性分析方法[J].中国安全科学学报,2001,11(3):6-8.
[2]王遥,高平校,沈祖培,黄祥瑞.人的认知可靠性模型分类及实验研究[J].核动力工程,2004,25(6):542-545.
[3]张力,黄曙东,杨洪,等.岭澳核电站人因可靠性分析[M].北京:中国核工业音像出版社,2001:3-15.
[4]肖国清,温丽敏,陈宝智,等.建筑物火灾中人行为的可靠性模型[J].东北大学学报:自然科学版,2002,8(23):761-764.
[5]何旭洪,黄祥瑞.工业系统中人的可靠性分析:原理、方法与应用[M].北京:清华大学出版社,2007:7-12.
[6]李子奈,潘文卿.计量经济学[M].北京:高等教育出版社,2009:74-75.
[7]Damodar N G,Dawn P.Basic Econometric[M].5 版.费剑平,译.北京:中国人民大学出版社,1995:277-288.
[8]Akaike,Hirotsugu.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control,1974,19(6):716-723.
[9]R Core Team(2014).R:A language and environment for statistical computing.R Foundation for Statistical Computing,Vienna,Austria[OL].http://www.R-project.org/.3600.
