基于流形学习的面向对象的软件缺陷预测模型

石陆魁，马春娟，王靖鑫，周 浩

（河北工业大学 计算机科学与软件学院，天津300401）

0 引 言

在面向对象的软件缺陷预测中，大部分模型基于分类算法，如BP神经网络 （back propagation network，BP）［1］、朴素贝 叶 斯 （naive Bayesian，NB）［2］、支 持 向 量 机 （support vector machine，SVM）［3，4］、K 近 邻 法 （K－nearest neighbors，KNN）等。在软件缺陷预测中，通常根据某种软件度量模型来获得相关数据，然后利用分类方法进行预测。但对于面向对象的软件，为了更好地描述软件的特性，需要用更多的属性来度量软件，导致数据的维数越来越高。随着数据维数的增加，最大限度地预测软件中存在的缺陷变得较为困难，产生了所谓的 “维数灾难”问题。因此，为了更准确地预测面向对象的软件中存在的缺陷，提高软件质量，对高维的软件度量数据进行降维处理是非常必要的［5］。而流形学习作为一种处理高维数据的重要技术，可以发现隐藏在高维数据中的真实结构。流形学习方法分为线性和非线性方法，线性方法如主成分分析法 （principal component analysis，PCA）等，非线性方法如等距映射法（isometric mapping，ISOMAP）、局域线性嵌入法 （locally linear embedding，LLE）、拉普拉斯特征映射法 （Laplacian eigenmaps，LE）、局部切空间校正法 （linear local tangent space alignment，LTSA）等［6］，这些非线性方法都可以较好地将高维数据映射到低维空间中，并得到了广泛的应用［7－11］。通过将流形学习引入到面向对象的软件缺陷预测中，有效地提高了缺陷的预测精度和效率。

1 相关工作

1.1 C＆K 度量

软件缺陷在软件工程领域是指可运行产品中会导致软件失效的瑕疵，开展软件缺陷预测的目的是帮助软件开发人员更有效地提高发现和排除缺陷的效率，从而减少软件产品中的缺陷，达到提高软件产品的有效性和可靠性的目的。软件度量是与软件缺陷预测密切相关的一个概念，指软件生产过程和软件产品的属性，其实质是根据一定的规则，量化实体属性，有效描述和理解软件产品。软件度量的目的是用软件度量学科学地对软件质量进行评价，帮助制定切实可行的开发计划，合理利用资源，有效控制和管理开发过程，从而提高软件质量，降低开发成本。传统的软件度量模型包括McCabe结构复杂性度量、Halstead软件科学度量、LOC 语句行度量和Woodward度量等，它们都是针对传统的面向结构化的软件开发过程。软件缺陷预测则是通过软件度量来指导软件开发过程中资源的分配，帮助开发人员发现缺陷，找出相应的解决方案，提高软件产品的质量。

随着面向对象技术的广泛应用，传统的度量模式无法度量面向对象的编程中的数据抽象、封装、继承、多态、信息隐藏等特性，需要研究面向对象的软件度量模型。目前，主要的面向对象的软件度量模型有：C＆K 度量模型和MOOD 模 型 等［12－14］。C＆K 度 量 模 型 给 出 了6 个 类 级 别 的度量指标：每个类的加权方法数 （weighted methods per class，WMC）；继 承 树 的 深 度 （depth of inheritance，DIT）；类的孩子数目 （number of children，NOC）；对象类之间耦合 （coupling between object classes，CBO）；一个类的响应集 合 （response for a class，RFC）；类 内 聚 缺 乏 度（lack of cohesion in methods，LCOM）。该模型能较好好地反映面向对象技术的本质特点，设计者可以根据这6个指标的度量值调节设计的灵活度，指导类的设计。由于MOOD 模型受环境影响较大，所以应用较少。在实验中选择基于C＆K 度量模型对面向对象软件的缺陷进行预测。

1.2 LE算法

LE算法是一种基于谱图理论的流形学习算法，其基本思想是在高维空间中离得很近的点投影到低维空间中的像也应该离得很近，LE算法最终归结为求解图拉普拉斯算子的广义特征值问题［6］。设集合X＝ ｛X1，X2，…，Xn｝是D 维空间RD中的一个数据集，LE算法的主要步骤如下［6］：

（1）构造邻域图。使用ε邻域或k 近邻方法计算每个样本点Xi的邻域并构造邻接矩阵G。

（2）建立加权邻接矩阵W。为邻域图中的每条边选择一个权值，有2种方法。一种是使用0／1核，如果样本点i和j 有边连接，即Gij＝1，则Wij＝1，否则Wij＝0；另一种是热核方程，如果Gij＝1，则Wij＝exp（－d2ij／σ2）；否则Wij＝0。

（3）求解广义特征问题。通过求解稀疏矩阵的特征值问题来求出最优解，图G 的拉普拉斯矩阵定义为L＝DW，其中D 为对角矩阵且Dij＝∑jWij，L 为拉普拉斯算子。将广义特征方程中d 个最小特征值对应的特征向量作为嵌入空间的坐标Y。

LE算法侧重于保持流形的局部邻域结构，是一种局部的非线性方法，能够反映数据集映射到低维空间的内在几何结构，可以用于数据的聚类处理。该算法的特点在于将问题最终转化为求解图拉普拉斯算子的广义特征值问题，不仅简化了求解过程，而且大大提高了运行速度。

1.3 软件缺陷预测方法

不同的软件缺陷预测模型使用了不同的预测技术，目前常用的软件缺陷预测技术大部分是基于分类算法的，如K 近邻、朴素贝叶斯、支持向量机、BP神经网络等。实验中使用这4种分类方法作为预测方法，下面简要地介绍一下这些方法。

1.3.1 K 近邻法

K 近邻法的基本思路是：在训练集中找出k 个与待测样本距离最近的样本，计算每一个待测样本属于每类的权重，如下所示

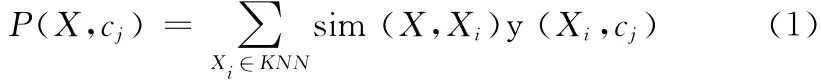
式中：X——测试样本的特征向量，sim（X，Xi）——相似度计算公式，y（Xi，cj）——类别属性函数，当样本Xi属于类cj时，函数值为1，否则为0。然后比较权重值，将测试样本分到权重最大的一类中。

1.3.2 朴素贝叶斯法

朴素贝叶斯分类法基于概率统计的思想，假定各决策变量是相互独立的，通过统计现有数据和已知的先验知识，使用概率统计的手段预测未来某一事件可能发生的概率。假设X＝ ｛x1＝A1，x2＝A2，…，xn＝An｝为观测样本，假定可以将样本分为m 个类，用c1，c2，…，cm表示，当且仅当满足如下公式时，未知样本X 通过贝叶斯分类模型将其分为ci

P（ci｜X）＞P（cj｜X），1≤j≤m，j≠i （2）

式中：ci——P（ci｜X）的最大值对应的类也称为最大后验假定。

为了计算P（ci｜X），由全概率公式可知

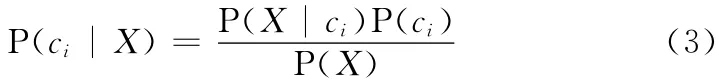
式中：P（ci）——先验概率。

为了解决数据集属性较多时计算P（X｜ci）开销非常大的问题，朴素贝叶斯理论提出类条件独立的假定，这样简化了联合分布，降低了P（X｜ci）的计算开销，P（X｜ci）的计算可简化为

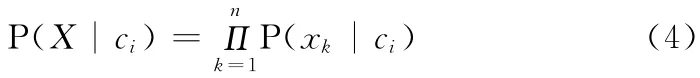
式中：P（x1｜ci），P（x2｜ci），…，P（xn｜ci）由训练样本估计，其计算方法如下

式中：Sik——类ci中属性Ak的值为xk的训练样本数。

1.3.3 支持向量机

支持向量机分类通过在高维空间中寻找最优的分类超平面将两类样本尽可能多地正确分开，同时使分开的两类样本距离该超平面最远。支持向量机的关键在于核函数，它将向量映射到高维空间中。对二分类问题，给定 ｛（X1，y1），…，（Xl，yl）｝为线性可分样本集，其中Xi∈Rn，yi∈ ｛＋1，－1｝，i＝1，2，…，l。SVM 求最优分类面问题可以转化为二次规划问题，如下所示

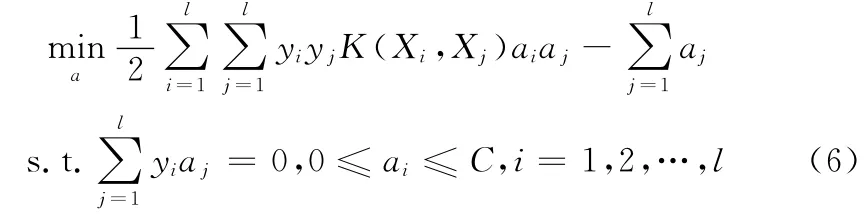
式中：αi和αj——拉格朗日乘子，K （Xi，Xj）——核函数，它是连接低维与高维之间的桥梁。求解方程式得：

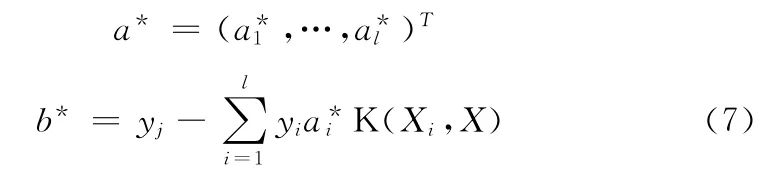
式中：b＊——最优超平面的偏移量。根据支持向量机求得决策函数如下

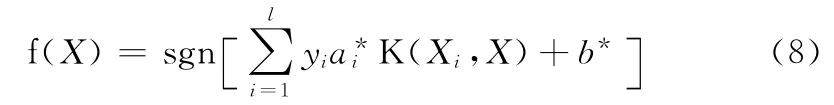
在 实 验 中 使 用 径 向 基 核 函 数 （radial basis function，RBF），其定义如下

式中：X 和X′——特征向量，σ决定径向基核函数的带宽。

1.3.4 BP神经网络

误差反向传播神经网络BP通过反向传播反复调整网络的权值和偏差，使输出模式尽可能地接近期望模式，当输出层的误差平方和小于指定误差时训练完成。算法包括以下几个步骤：

（1）初始化网络及学习参数，设定神经元阈值，初始化隐含层与输出层各节点的连接权值为 ［－1，1］区间的一个随机数。

（2）提供训练模式，选择一个期望输出不满足要求的训练模式，将其输入模式和期望输出传递给网络。

（3）正向传播过程，对给定的输入模式，计算从第一隐含层开始的输出模式，比较得到的输出模式与期望模式，若误差不满足要求，则执行步骤 （4）；否则，执行步骤（6）。

（4）反向传播过程，从输出层反向计算到第一隐含层，并逐层修正各单元的连接权值。首先计算同一层单元的误差δk，然后按照下式修正相应的权值

（5）返回步骤 （3）。

（6）如果所有训练模式都满足期望输出，训练结束；否则，返回步骤 （2）。

2 基于流形学习的缺陷预测模型

为了更好地度量面向对象软件的特性，面向对象的软件度量模型中包含的属性越来越多，导致度量数据的维数越来越高，直接对这些高维的软件度量数据进行软件缺陷预测，不但会影响预测的精度，而且会降低预测算法的执行效率。如果使用流形学习算法对高维的软件度量数据进行降维，提取出其与分类类别相关的本质特征，无疑会提高软件缺陷的预测精度，而且会提高算法的执行效率。基于此提出了基于流形学习的面向对象的软件缺陷预测模型，如图1所示。

在该模型中，首先对原始的度量数据利用流形学习方法进行降维处理，得到低维特征，然后将低维特征数据分为训练集和测试集，在训练集上训练建立预测模型，最后在测试集上测试预测模型的有效性。流形学习方法可以采用PCA、MDS、ISOMAP、LLE、LE和LSTA 等，预测方法可以采用KNN、BP神经网络、NB、SVM 等。

3 实验结果

在2个数据集上验证所提模型的有效性，一个是KC1数据集［15］，包含145个样本，每个样本有89个度量属性，其中包括CK 度 量 集 的 属 性 如 WMC、NOC、DIT、CBO、RFC、LCOM 等。另 一 个 是Eclipse2.0 数 据 集［16］，有6728个样本，从中抽取了200个样本。样本标签分两类，没有缺陷的软件模块用 “1”表示，有缺陷的软件模块用 “2”表示。在实验中采用二折交叉验证法，将每个数据集平均分成2个子集，轮流将其中一个子集做训练集，另一个子集做测试集，取2次的均值。使用精度（accuracy）、查准率 （precision）、查全率（recall）和F值来评价模型的预测能力。

在实验中，首先用KNN、NB、SVM 和BP 神经网络直接对高维的软件度量数据进行预测；然后利用PCA 方法将高维数据映射到低维空间中，再用4种分类方法对低维数据进行预测；接着利用LE 算法得到高维数据的低维表示，再用4种分类方法对低维数据进行预测；最后比较不同方法得到的结果。在实验中，SVM 模型类型采用CSVC模型，核函数采用径向基核函数。在KC1 数据集上，LE算法中k＝4 和d＝5，PCA 算法中主成分个数为5，SVM 算法中C＝1和σ＝0.01176，实验结果见表1。在Eclipse2.0数据集上，LE算法中k＝8和d＝6，PCA 中主成分个数为5，SVM 算法中C＝1 和σ＝0.04167，实验结果见表2。

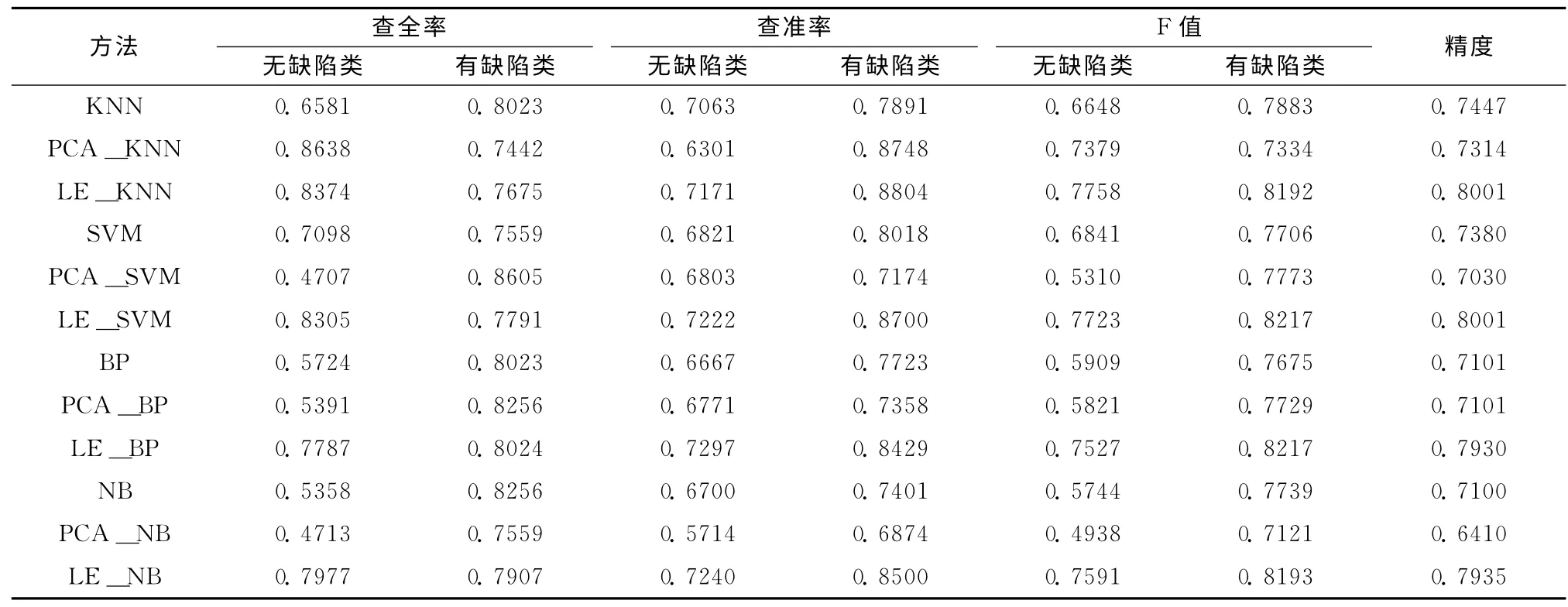
表1 在KC1数据集上的结果

表2 在Eclipse2.0数据集上的结果

通过上述实验可以看出，与直接对原始的软件度量数据预测相比，用LE 算法降低维数后再预测具有更高的精度，而利用PCA 降维后多数情况下与直接预测的结果相近。同时，用4种方法直接对高维数据进行预测时，4种方法的预测结果相差较大，KNN 方法的预测精度最高。而降维后再用4种方法进行预测得到的结果非常相近，说明降维后采用何种预测方法对预测结果的影响不大。因此，利用所提出的模型提高了软件缺陷预测的精度，这样有助于软件开发团队在软件开发周期的前期更准确地预测软件缺陷的分布，可以更好地帮助软件开发团队将有限的资源集中于容易出现缺陷的高风险模块，以有效预防因前期模块的缺陷带来更多的漏洞，避免了后期测试时发现错误而需要花费大量时间和影响经济效益的问题，可以更好的确保软件如期保质保量地完成。

此外降维后再预测所用的时间明显减少，算法的执行效率得到极大地提升。不同预测方法在2个数据集上降维前后的执行时间如表3和表4所示。每种方法所用时间为十次执行的平均值，单位为秒／s。

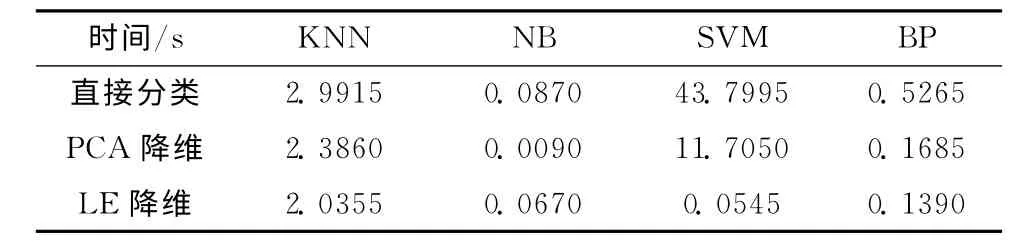
表4 各种预测方法在Eclipse2.0上的执行时间

4 结束语

为了有效地度量面向对象的软件，需要用更多的度量属性来描述。对于高维的软件属性度量数据，传统的软件缺陷预测方法会产生 “维数灾难”问题。本文结合流形学习提出了一种基于流形学习的面向对象的软件缺陷预测模，其基本思想是利用流形学习方法降低数据的维数后再利用分类算法预测软件中存在的缺陷。实验结果表明该模型有效地提高了软件缺陷预测的精度和效率。下一步的工作是研究如何将该模型应用在实际的软件开发过程中，来指导实际的软件开发。

［1］LI K，GONG L，KOU J.Predicting software quality by fuzzy neural network based on rough set［J］.Journal of Computational Information Systems，2010，6 （5）：1439－1448.

［2］GE Hehe，JIN Cong，YE Junmin.Software defect prediction model based on particle swarm optimization and nave Bayes［J］.Computer Engineering，2011，37 （12）：36－37 （in Chinese）.［葛贺贺，金聪，叶俊民.基于PSO 和朴素贝叶斯的软件缺陷预测模型 ［J］.计算机工程，2011，37 （12）：36－37.］

［3］WANG Tao，LI Weihua，LIU Zun，et al.Software defect prediction model based on support vector machine［J］.Journal of Northwestern Polytechnical University，2011，29 （6）：864－870 （in Chinese）.［王涛，李伟华，刘尊，等.基于支持向量机的软件缺陷预测模型 ［J］.西北工业大学学报，2011，29 （6）：864－870.］

［4］JIANG Huiyan，ZONG Mao，LIU Xiangying.Research of software defect prediction model based on ACO－SVM ［J］.Chinese Journal of Computers，2011，34 （6）：1148－1154 （in Chinese）. ［姜慧研，宗茂，刘相莹.基于ACO－SVM 的软件缺陷预 测 模 型 的 研 究 ［J］.计 算 机 学 报，2011，34 （6）：1148－1154.］

［5］LU H，Cukic B，Culp M.Software defect prediction using semi－supervised learning with dimension reduction ［C］／／Proceedings of the 27th IEEE／ACM International Conference on Automated Software Engineering，2012：314－317.

［6］Tsai FS.Comparative study of dimensionality reduction techniques for data visualization ［J］.Journal of Artificial Intelligence，2010，3：119－134.

［7］LIU Jinling.Chinese short messages text clustering algorithm based on ISOMAP ［J］.Computer Engineering and Application，2009，45 （34）：144－146. ［刘金岭.基于ISOMAP 的中文短信文本聚类算法 ［J］.计算机工程与应用，2009，45（34）：144－146.］

［8］QIAN Jin，DENG Kazhong，FAN Hongdong.Dimensionality reduction and classification for hyperspectral remote sensing imagery based on Laplacian Eigenmap ［J］.Remote Sensing Information，2012，27 （5）：3－7 （in Chinese）. ［钱进，邓喀中，范洪冬.基于拉普拉斯特征映射高光谱遥感影像降维及其分类 ［J］.遥感信息，2012，27 （5）：3－7.］

［9］WU Qiang，WANG Xinsai，WANG Weiping，et al.Infrared imaging colorizing method based on local linear embedding ［J］.Journal of Applied Optics，2012，33 （4）：733－737 （in Chinese）.［吴强，王新赛，王卫平，等.基于LLE的红外成像彩色 化 处 理 算 法 研 究 ［J］. 应 用 光 学，2012，33 （4）：733－737.］

［10］XIANG Tingting，LUO Yunlun，WANG Xuesong.Application of manifold learning and nonlinear dimensionality reduction in private preserving ［J］.Computer Engineering and Applications，2011，47 （8）：79－83 （in Chinese）. ［向婷婷，罗运纶，王学松.流形学习及维数约简在数据隐私保护中的应用［J］.计算机工程与应用，2011，47 （8）：79－83.］

［11］CUI Y，ZHENG C，YANG J.Dimensionality reduction for microarray data using local mean based discriminant analysis［J］.Biotechnology Letters，2013，35 （3）：331－336.

［12］YI Tong.Software measurement study in object－oriented design：State of art ［J］.Application Research of Computers，2011，28 （2）：427－434 （in Chinese）.［易彤.面向对象设计中软件度量学：回顾与热点 ［J］.计算机应用研究，2011，28 （2）：427－434.］

［13］ZHANG Yan，LIN Ying，WANG Hongsong.Study on object－oriented software metrics［J］.Computer and Digital Engineering，2009，37 （3）：117－119 （in Chinese）.［张雁，林颖，王红崧.面向对象软件度量的研究 ［J］.计算机与数字工程，2009，37 （3）：117－119.］

［14］TAO Min，TAO Shi.Research on software metrics method for object oriented C＋＋based ［J］.Software Industry and Engineering，2010，4：40－44 （in Chinese）. ［陶敏，陶石.基于C＋＋语言的面向对象的软件度量方法研究 ［J］.软件产业与工程，2010，4：40－44.］

［15］Boetticher G，Menzies T，Ostrand T.Promise repository of empirical software engineering data ［DB／OL］. ［2007－01－01／2013－03－17］.http：／／promisedata.org／repository.

［16］Zimmermann T，Premraj R，Zeller A.Predicting defects for eclipse［C］／／In Proceedings of the 3rd International Workshop on Predictor Models in Software Engineering，2007.