GNSS系统中检测与判决的研究

欧松林，李金海，袁建国，孙金海，阎跃鹏

（1.重庆邮电大学 光纤通信技术重点实验室，重庆400065；2.中国科学院微电子研究所，北京100029）

0 引 言

GNSS（global navigation satellite system）的捕获系统通常包括相关峰的计算、信噪比的提升、检测与判决3个部分，而检测与判决部分的作用是判断系统是否捕获到信号以及确定系统的检测概率。检测与判决部分通常包含很多种形式，如单次检测、多次的唐检测以及系统检测等。

文献［1－7］主要阐述了单次检测和唐检测的检测概率并给出了相关的性能分析，但这些检测判决的分析却没有结合整个系统进行分析。系统检测概率是整个捕获系统性能评价的一个重要指标，它不仅依赖于系统中每个单元的单次检测概率，而且还和捕获策略息息相关。系统检测分析方法最早来源于扩频通信中关于检测概率的讨论，文献［8，9］首先提出了扩频通信中最大值检测算法，接着文献［10］将最大值分析方法引入到GNSS系统中，主要分析了最大值捕获策略下的系统检测概率、系统漏检概率等。但最大值策略下的系统性能却不太理想，存在系统检测概率较低和系统漏检概率高的问题。

为了解决这一问题，本文首先分析了单次检测概率和虚警概率，然后从概率的角度以最大值捕获策略为例分析了GNSS的系统检测概率、系统漏检概率、系统虚警概率；最后本文提出了两种常见GNSS系统中关于检测概率低和漏检概率高这一问题的解决方法，并给出了相应的仿真结果。

1 单次检测与判决

假设事件H0表示检测卫星不存在，输入信号中仅有噪声；H1表示检测卫星存在，输入信号中既有信号部分也有噪声部分；同时假设单次检测的门限值为Vt。这样单次检测概率和单次虚警概率可以表示成如下形式［1］

由文献［2］可知采用平方律检波时f（x｜H1）是服从非中心卡方分布，f（x｜H0）是服从中心卡方分布，因此可以用信噪比来表示上述关系，得到如下表达式

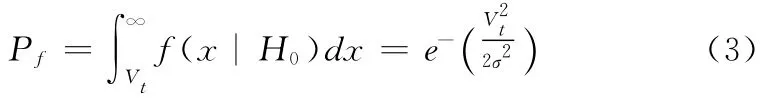
从而得到单次检测门限值为

将式（4）代入式（2）可以得到检测概率的表达式

式中：A2／σ2和信噪比SNR 是由直接关系的，而这个信噪比又和相干积分时间是由关系的，因此就直接把相干积分时间、信噪比和检测概率相互联系了起来，其表达式为

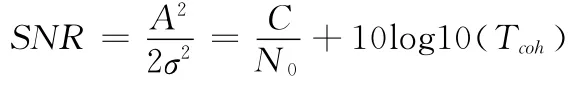
式中：I0（·）——修正的第一类零阶贝塞尔（Bessel）函数，Qk——广义k阶Marcum Q 函数。

2 系统检测与判决

对GNSS系统来说，捕获是一个对多普勒频移和码相位的二维搜索过程。假设码相位的个数为H，多普勒频的个数为L，系统的捕获过程相当于要检测一个由M＝HL 个单元组成的整体，其中每个单元都具有和单次检测相同的检测概率pd、虚警概率pf。我们定义系统检测概率为PD，系统虚警概率为PFA，系统漏检概率为PMD，在下文中将采用PD、PMD和PFA为主要指标对系统性能进行评价。为了更好的建模分析，假设概率分布符合如下约束：

（1）符合H1分布的单元最多只有一个，这个单元被记为XA，这就意味着在整个搜索空间中只有一个XA，其概率分布为fA（x）；

（2）除去符合XA的单元，其余的单元随机变量符合假设H0，这些单元被记为Xn，其概率分布为f0（x）；

（3）随机变量XA均匀分布在整个搜索空间中，其出现在任意一个单元中的概率为1／M；

（4）搜索空间中的所有单元都是相互独立的。

基于上面的假设，本文以最大值捕获策略为例，分析GNSS的系统检测与判决。所谓最大值捕获策略就是计算出整个搜索空间中所有码相位和多普勒频移的相关函数，找出其中的最大值，并对最大的相关峰进行判决。如果相关峰的最大值比门限值大，那么就认为卫星被捕获到，并且通过相关峰出现的位置可以计算出码相位和多普勒频移。

2.1 最大值捕获策略的系统检测概率

从上面的最大值捕获介绍中可以看出如果采用最大值捕获，只有当XA所在的相关峰为整个搜索空间中的最大值且这个值超过门限值时，才能被系统检测到。因此系统检测概率PD可以写成如下形式

式中：Vt——判决门限。从XA的定义中可以知道当XA的值是最大值，同时其值大于或者等于其它所有随机变量时上式可以取等号，因此有下式

由式（6）、式（7）可以得到

从上面得到的随机变量的分布可以得到检测概率的表达式如下

式中：除了XA＝Xn的一项外，其它的M－1 项都相等，所以式（9）中的相等项可以写成

当XA＝Xn时，其表达式为

因此系统检测概率为

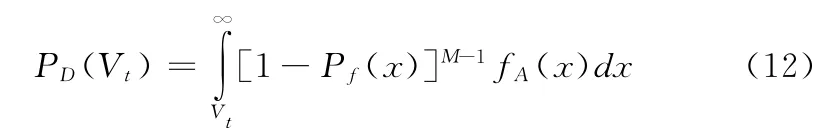
当Pf（Vt）非常小且M 非常大时，检测概率可以简化成如下形式

2.2 最大值捕获策略的系统漏检概率

系统漏检出现在卫星存在却没有被检测到，换句话说就是每个单元的相关峰值都比门限值小时才会发生漏检。这时漏检概率跟采用的捕获策略无关，因此系统的漏检概率可以表示为

式中的乘积项同样有M－1项相同，它们是XA不在的单元，另外一项是XA＝Xn时的单元，所以可以得到下式

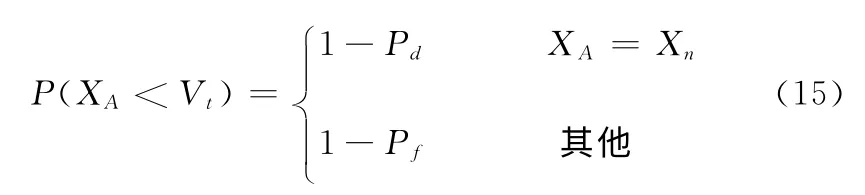
所以系统的漏检概率可以表示成

2.3 最大值捕获策略的系统虚警概率

系统的虚警概率是指检测判决输出错误的概率，这就意味着噪声单元的相关峰值超过门限值。单次虚警概率通常指的是没有信号时的虚警概率，而系统虚警概率除了没有信号时的虚警概率外，还有信号存在时的虚警概率。为了避免相互混淆，我们用PaFA表示信号不存在时的虚警概率，用PpFA表示信号存在时的虚警概率。信号存在时的虚警概率指的是卫星存在，但系统却错误的判决了卫星信号存在的位置。本文分别给出了两种系统虚警概率的表达式，首先分析信号不存在时的系统虚警概率。

最大值捕获时，当M 个单元的相关峰值超过门限值Vt时就会产生错误判决，所以信号不存在时的系统虚警概率变为如下形式

接着分析信号存在时的虚警概率。根据定义可知，当信号存在时系统的虚警概率表明XA不是M 个单元的相关峰的最大值，但是最大相关峰值却超过了门限值Vt。因此PpFA可以写成如下形式

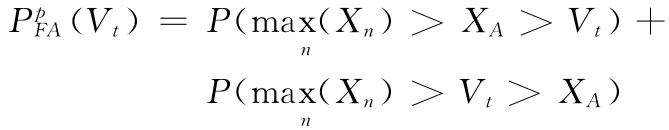
由前面的概率分布可以将PpFA表示为

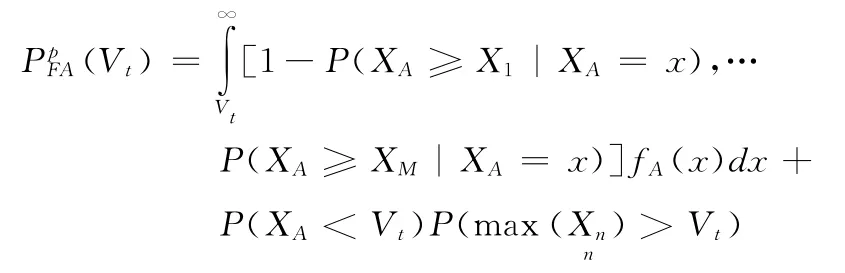
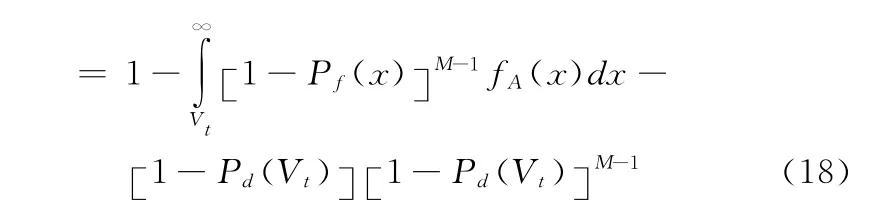
观察式（18）可以发现式中的第2项和第3项与前面关于系统检测概率和系统漏检概率的公式相同，因此PpFA可以简写成如下的形式

式 （19）和前文关于PpFA的定义是相一致的，即1－PD－PMD表示XA不是M 个单元的相关峰的最大值，但是最大相关峰值却超过了门限值Vt。式 （19）说明信号存在时的虚警概率只依赖于系统检测概率和系统漏检概率。

3 仿真分析

为了得到第二节中相关结论的仿真分析结果，需要知道单次检测概率、单次虚警概率和概率密度分布，将式（3）、式（5）归一化后可以得到单次检测概率和单次虚警概率，式（20）则说明了XA的概率密度分布

式中：λ——归一化后的信噪比，其值为λ＝2SNR，β是归一化后的系统门限。

将式（20）、式（21）、式（22）代入式（12）可以得到最大值捕获策略下的系统检测概率

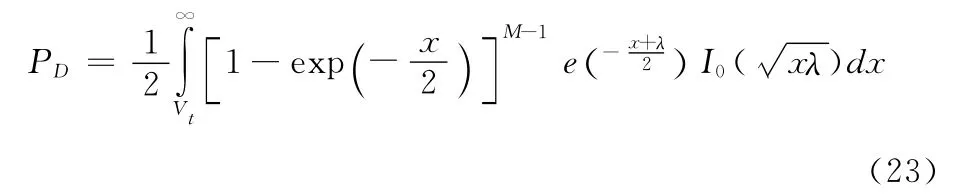
将式（21）、式（22）代入式（16）可以得到最大值捕获策略下的系统漏检概率

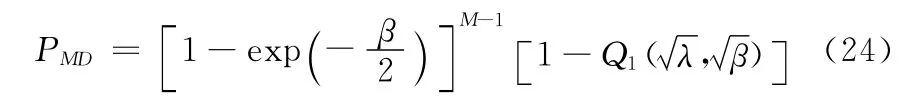
为了得到系统检测概率、系统漏检概率、有信号时的虚警概率和无信号时的虚警概率之间的关系，本文采用蒙特卡洛仿真得到性能曲线。其中参数设置为载噪比取实际环境中常见的40dB－Hz，相干积分时间为1ms，仿真时采用的总的搜索单元M＝2046，即码相位方格H＝186，多普勒频移方格L＝11。

仿真分为两步，首先假设一定的无信号时系统总的虚警概率，由式（17）可以得到各搜索策略下的单次虚警概率，将单次虚警概率代入式（21）得到门限值，从而由式（22）推出单次检测概率；第二步将得到的单次虚警概率、单次检测概率、门限值代入式（23）、式（24）可以得到最大值捕获策略下的系统检测概率和系统漏检概率，然后画出曲线得到图1、图2和图3。为了能对比说明最大值捕获策略和其它捕获策略的不同，我们在图1到图3中加入了顺序捕获策略的仿真结果，所谓顺序捕获就是按顺序计算出每一个单元的相关峰，一旦一个单元的相关峰值被计算出来，则立刻与门限值进行比较。如果相关峰值超过门限值，就认为卫星被捕获到，其它剩余的搜索单元就停止搜索。

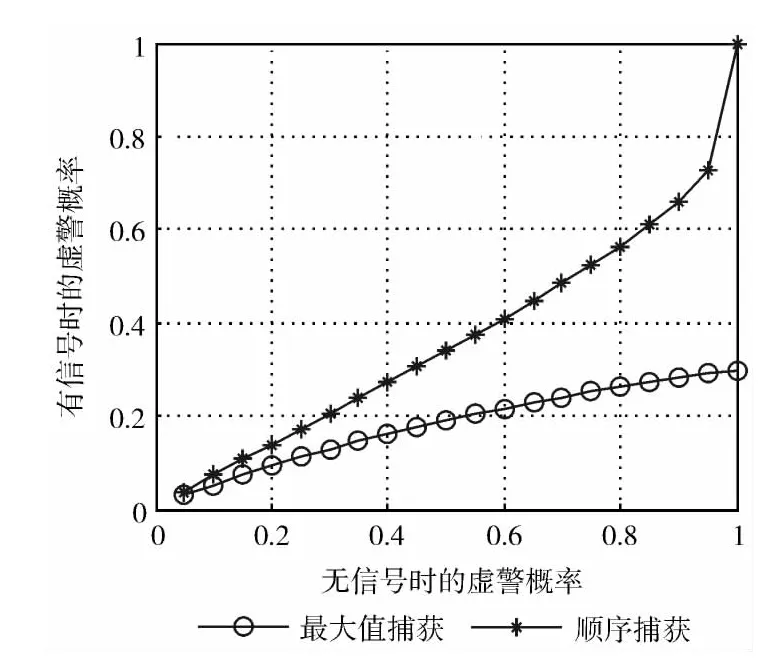
图1 PaFA 和PpFA 之间的关系

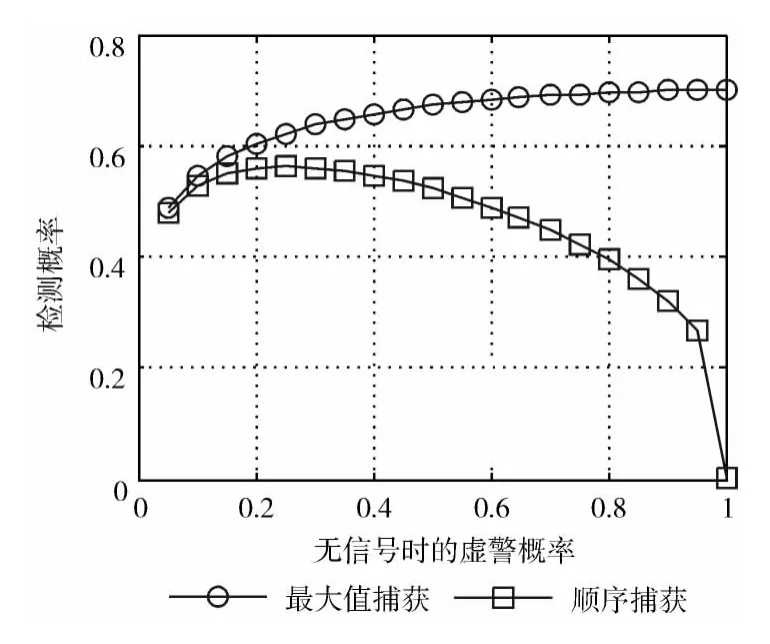
图2 PaFA 和PD 之间的关系

图3 PaFA 和PMD 之间的关系

从图1中可以看出有信号时的虚警概率随着无信号时的虚警概率的增加而增加，并且很明显的可以看出对于任意门限值，无信号时的虚警概率总是大于有信号时的虚警概率。造成这一现象的根本原因在于门限值是根据无信号时的虚警概率推导出来的，而门限值对有信号时的虚警概率也有着巨大的影响。

衡量一个系统性能好坏的一个重要指标就是ROC（receiver operating characteristic）曲 线，而 图2 画 出 了 系 统 检测概率和无信号时的虚警概率的ROC 曲线，图3画出了系统漏检概率和无信号时的虚警概率的ROC 曲线。从图2中可以看出最大值捕获的检测概率随着虚警概率的增加而增加，但顺序捕获的检测概率却随着虚警概率的增加而减少，这说明最大值捕获的检测概率和虚警概率同时随着捕获门限的减小而增大，也就是说不能通过简单的改变门限值的设定而提高检测性能，这个和单次检测是的结论是一致的。而顺序捕获则正好相反，检测概率和虚警概率随着门限值的减小而减小。从图3中可以看出系统的漏检概率随着虚警概率的增加而降低，虚警概率增加说明系统错误的检测到了信号，那么漏检概率必然减少。综合图2和图3可以看出当载噪比为40dB－Hz，系统虚警概率为0.05时，单次虚警概率为1×10－6，这个虚警概率在单次检测中性能良好。但我们发现这时的系统检测概率却仅为47%，而系统的漏检概率却高达45%，很显然这种程度的性能指标对于GNSS接收机的捕获系统来说是不能接受的。为了解决这一问题，本文提出了以下两种方法。

其中一种方法是提高整个系统的接收载噪比，具体方法可以通过延长相干积分时间、增加非相干积分次数以及引入差分相干来实现。根据相干积分、非相干积分的理论可知，多增加一倍的相干积分时间就能够得到3dB 的信噪比增益，而增加两倍非相干积分就能得到2.6dB 左右的信噪比增益。这种方法相对于普通的GNSS接收机来说仅仅增加了几毫秒的总积分时间，基本上不影响定位时间，因此该方案是可行的。我们改变系统的载噪比为42dB－Hz，其它参数不变，如图4所示。

图4 增加载噪比后PaFA 和PD 之间的关系

从图4中可以明显的看到载噪比为42dB－Hz、虚警概率为0.05 时，系统检测概率接近90%，相对于载噪比40dB－Hz时，系统性能有了较为明显的改善。这个检测概率和虚警概率在普通的GNSS接收机系统中是可以接受的。很显然随着系统检测概率的增加，系统的漏检概率也会随之降低。因此我们可以到以下结论：在同样虚警概率的条件下，载噪比的提高不仅可以提高单次检测概率，也能够提高系统检测概率。

另一种方法是在系统中结合多种检测算法，如在系统检测概率中增加唐检测算法或者增加N 中取M 算法，在此仅分析增加唐检测算法后的系统性能。以顺序捕获为例，增加唐检测算法的流程如下：每个单元的单次检测后的相关峰并不马上与门限值进行比较，而是在其后接上一个唐检测算法模块。如果相关峰值经过多次搜索过后没有达到门限值，则认为信号捕获失败，继续搜索下一个单元；反之如果唐检测过程中相关峰值多次超过门限值，那么就认为信号捕获成功，然后终止整个系统的搜索。设置系统信噪比为40dB－Hz，其它参数和前文相同，如图5所示。

图5 增加唐检测算法后PaFA 和PD 之间的关系

从图5中可以看出增加唐检测算法后，系统虚警概率为0.05时，系统的检测概率已经超过90%，这个方法比提高信噪比到42dB－Hz所获得的系统性能改善还要大。就实现复杂度而言，常见的GNSS接收机都会在单次检测后增加捕获确认算法，可以采用多个通道同时并行处理。因此这种方法对于系统硬件来说并没有较大的改动，仅需要针对每种不同的检测策略对原有的唐检测算法稍加改动即可。

4 结束语

本文以最大值策略下的系统检测概率、系统虚警概率和系统漏检概率为研究对象，根据概率论的相关理论基础，得到了系统检测概率、系统虚警概率和系统漏检概率的表达式，分析了其和单次检测概率之间的关系，利用无信号时的虚警概率推导出有信号时的虚警概率的表达式，在GNSS接收机的设计中必须要考虑到这两种虚警概率共同的影响。最后利用蒙特卡洛方法进行了MATLAB 仿真，得到如下结论：

（1）捕获策略不影响系统的漏检概率；

（2）有信号时的虚警概率随着无信号时的虚警概率的增加而增加，且对于任意门限值，无信号时的虚警概率总是大于有信号时的虚警概率；

（3）最大值捕获的检测概率随着虚警概率的增加而增加，但顺序捕获的检测概率却随着虚警概率的增加而减少。最大值捕获的检测概率和虚警概率同时随着捕获门限的减小而增大，而顺序捕获则正好相反。系统的漏检概率随着虚警概率的增加而降低；

（4）提高接收信号的载噪比和增加唐检测算法都能够明显的提高系统的检测性能和减少系统的漏检概率。

文中得到的一系列结论为GNSS捕获系统在实际环境中的运用提供了一定的理论依据。

［1］XIE Gang.Principles of GPS and receiver design ［M］.Beijing：Publishing House of Electronics Industry，2011 （in Chinese）.［谢钢.GPS原理与接收机设计 ［M］.北京：电子工业出版社，2011.］

［2］Kaplan E.Understanding GPS principles and applications ［M］.2nd ed.KOU Yanhong，transl.Beijing：Publishing House of Electronics Industry，2012（in Chinese）.［Kaplan E.GPS原理与应用［M］.2版.寇艳红，译.北京：电子工业出版社，2012.］

［3］Wang Jun，Wu Siliang，Yuan Qiao，et al.Direct acquisition method of GPS P code and its parameter optimization ［C］／／International Conference on Communications and Mobile Computing，2010：469－475.

［4］LI Sichao，YE Tianchun，XU Jianhua.Analysis on resident time and detection performance of tong detector［J］.Electronic Measurement Technology，2009，34 （3）：53－55 （in Chinese）.［李思超，叶甜春，徐建华.唐检测器驻留时间及其性能分析 ［J］.电子测量技术，2009，34 （3）：53－55.］

［5］Yen NY，Su SL.Robust matched－filter acquisition for directsequence ultra wide band systems［J］.IEEE Trans on Vehicular Technology，2009，58 （8）：4419－4452.

［6］MU Rongzeng，LI Jinhai，YAN Yuepeng.An improved threshold setting algorithm for fast acquisition of GPS signals［J］.Journal of Harbin Engineering University，2009，30（11）：1291－1294 （in Chinese）. ［牟荣增，李金海，阎跃鹏.GPS信号快速捕获方案中门限设定算法 ［J］.哈尔滨工程大学学报，2009，30 （11）：1291－1294.］

［7］MA Lin，CUI Wei，WU Siliang.Improved tong multiple trial algorithm with near neighbor constraint in extremely low SNR condition ［J］.System Engineering and Electronics，2011，33（8）：1745－1749 （in Chinese）. ［马琳，崔嵬，吴嗣亮.极低信噪比环境下含近邻约束的改进唐检测判决算法 ［J］.系统工程与电子技术，2011，33 （8）：1745－1749.］

［8］Corazza GE.On the MAX／TC criterion for code acquisition and its application to DS－SSMA systems［J］.IEEE Transactions on Communications，1996，44 （9）：1173－1182.

［9］Park H，Kang B.On the performance of a maximum likelihood code acquisition technique for preamble search in a CDMA re－verse link ［J］.IEEE Transactions Vehicle Technology，1998，47 （1）：65－74.

［10］Borio D，Camoriano L，Lo Presti L.Impact of GPS acquisition strategy on decision probabilities［J］.IEEE Transaction on Aerospace and Electronic Systems，2008，44 （3）：996－1011.