基于模式搜索法高精度矫正钢轨磨耗测量的定位偏差
2014-12-21向文明
向文明,沈 钢
(同济大学铁道与城市轨道交通研究院,上海201804)
在钢轨打磨测量中需要了解打磨前后的轨顶打磨区域的打磨量,常采用手持式仪器对打磨前的钢轨廓形进行一次测量,然后再对打磨后的同一处钢轨廓形进行第二次测量,对比两次测量结果则能获得打磨的情况。由于仪器定位面在钢轨的下颚面上,虽然没有被打磨过,但由于钢轨表面生锈和定位精度问题会给磨耗量测量结果带来一定偏差。目前的接触式钢轨轮廓测量仪器相应的数值处理软件中没有相关功能以实现偏差的纠正,为此我们需要研究相关方法纠正这种偏差。

图1 钢轨廓型Fig.1 Rail profile
如图1(a)所示为先后两次的钢轨全断面测量结果。(注:文中所有插图的坐标单位和表格的数值单位均为:mm)。如果将前后测得的钢轨轮廓曲线在非磨耗区域拟合对齐即能矫正测量仪器的定位偏差。为此,截取第一次测量的钢轨廓型曲线的左侧下部曲线(图1(b)中的实线I);又截取第二次测量的左下侧下部曲线(图1(b)中的虚线II)。截取的实曲线I和虚曲线II为钢轨的非磨耗区段。如果能将图1(b)中的虚曲线II拟合回归到实曲线I中,然后再通过计算就可获得打磨量的准确值。本文提出一种能实现上述的曲线拟合回归过程的方法。
1 曲线偏离度量函数
为将II曲线拟合回归到I曲线中,只需将II曲线相对坐标轴作一定的横移、纵移及相对坐标原点旋转变换。因而可以说两曲线偏离度量函数F是关于坐标轴横移量X,纵移量Y及相对坐标原点旋转量alpha3 个自变量的函数。在两曲线有偏离的情况下F(X,Y,alpha)是大于0 的,当两曲线实现较好拟合时,F(X,Y,alpha)是接近于0的极小正数。理想条件下,两曲线能完全拟合则F(X,Y,alpha)等于0。找到合适的一组(X,Y,alpha)使得F(X,Y,alpha)接近于0即实现了曲线II较好的拟合回归到曲线I。为了便于利用计算机快捷、方便地实现曲线拟合回归,F(X,Y,alpha)的计算应便于编程实现。考虑到曲线是由有限个离散点组成的,本文提出一种利用曲线上的离散点之间的距离来衡量曲线偏差程度的方法。
曲线偏离度量函数F(X,Y,alpha)的算法:
假设曲线I 由m个离散点构成,曲线II 由n个离散点构成。用下述算法计算的返回值作为目标函数F(X,Y,alpha)的函数值。
1)对II曲线上的K=1,2,3,…,n个点做:
寻找I曲线上与第K点距离最近的Pk点和次最近点Qk点。由K点,Pk点和Qk点三点构成一个三角形。如果ΔKPkQk中∠PkKQk≤90°,则dk=‖KPk‖否则dk等于ΔKPkQk底边KPk上的高Hk。
2)曲线偏离程度F(X,Y,alpha)=()/n。
F(X,Y,alpha)值可以近似理解为II曲线上的所有点距离I曲线的平均间隙。举例说明:如图2,假设曲线II由a,b,c三点组成,曲线I由A,B,C,D四点组成。

图2 举例Fig.2 Example
图2所示状态下,与a点距离最近的两点分别为A,B;与b点距离最近的两点分别为B,C;与c点距离最近的两点分别为C,D;又∠AaB>90°,∠BbC>90°,∠CcD<90°故按算法,图示曲线II与曲线I的偏离度可表达为F(X,Y,alpha)=(Ha+Hb+‖Cc‖)/3。
2 偏差矫正优化算法
上述的曲线拟合问题归结于寻找一组最佳(X,Y,alpha)值使得两曲线偏离F(X,Y,alpha)最小,该问题为无约束最优化问题。无约束最优化问题有解析法和直接法两类求解方法。解析法需要计算目标函数的一阶导数甚至二阶导数,但有些无约束最优化问题的目标函数,其表达式比较复杂难以表达或者难以用明显的解析式表示出来,因而其导数很难求解或者无法得到,以致影响程序的编译。直接法只涉及目标函数值的计算不需要求解函数目标的导数,尽管可能因此影响到算法的效果,但选择得当,可以满足精度要求,同时因为编译方便,工程实际采用广泛。根据本文中问题的特点,决定采用模式搜索法进行求解。

图3 定位偏差矫正程序框图Fig.3 Positioning deviation correction program chart
2.1 模式搜索的基本思想
模式搜索法又名Hooke—jeeves 方法,于1961年提出。算法从初始基点开始交替实施两种搜索:轴向搜索和模式搜索。轴向搜索依次沿着n个坐标轴方向进行来,确定新的基点和有利于函数值下降的方向。模式搜索则沿着相邻两个基点的连线方向进行,试图使函数值下降得更快。
2.2 模式搜索算法
下述的ej=(0,···0,1,0,···,0)T,j=1,2,···,n,表示n个线性无关的搜索方向。
1)给定初始点x1∈Rn,初始步长δ,加速因子ω≥1,缩减率β∈(0,1),精度ε>0。令y1=x1,k=1,j=1。
2)轴向搜索:如果f(yj+δej)<f(yj) ,则令yj+1=yj+δej,转(3);如 果f(yj-δej)<f(yj) ,则 令yj+1=yj-δej,转(3);否则令yj+1=yj。
3)若j<n,则令j:=j+1,转(2)。如果f(yn+1)<f(xk),转(4);否则,转(5)。
4)模式搜索:令xk+1=yn+1,y1=xk+1+ω(xk+1-xk)。令k:=k+1,j=1,转(2)。
5)如果δ≤ε,停止,得到点x(k);否则,令δ:=βδ,y1=xk,xk+1=xk。令k:=k+1,j=1,转(2)。
2.3 基于模式搜索法的定位偏差矫正程序设计
模式搜索法是一种对初始解依赖度较高的优化算法,初始解选择不当可能会导致算法不能收敛于最优解。为避免上述问题,定位偏差矫正程序设计成多次调用模式搜索算法进行优化。某次优化结果不理想的情况下将以该次优化的结果作为下次优化的初值再次用模式搜索法优化,直到优化结果满足设定精度或前后两次优化结果的差异小于设定精度。定位偏差矫正程序的设计框图如图3所示。
3 测试与验证
3.1 仿真测试
采用科学计算软件MATLAB对程序编译。通过大量仿真实验表明基于模式搜索法的矫正方法能高精度的矫正定位偏差。仿真实验的计算机配置为P4/2.20GHz的CPU芯片、3.0G内存。为测试程序,分别用人工编制的理想测量曲线(图4(a))和正常仪器测得曲线(图4(b))进行了验证。同时为验证程序的运行速度和矫正的稳定性,在4(b)的情况下设定相同初始条件让程序仿真10次,求出程序的运行时间和矫正后曲线偏差的平均值及标准差(见表1)。结果表明,程序矫正快速且稳定,理想情况下的矫正精度极高,误差极小,图4(a)情况矫正后F(X,Y,alpha)=1.108×10-10。正常测量情况下也能将偏差矫正到测量仪器精度数量级内,图4(b)情况矫正后F(X,Y,alpha)=6.028×10-3。

图4 两种情况下的程序仿真实验Fig.4 Program simulation under two situations
3.2 仪器实测验证
通过模拟测量钢轨打磨量的过程,验证矫正方法的有效性。实验采用目前国内铁路部门普遍采用的高精度的钢轨外形测量仪器(图5),先对钢轨外形轮廓进行一次正常测量并获得轮廓曲线。然后在钢轨打磨轨顶区粘贴已知厚度的薄片并有意偏转测量仪器的定位位置后,对粘贴了已知厚度薄片的钢轨再次测量,并获得此时的轮廓曲线,如图6(a)。将先后测得轮廓曲线拟合后即可计算得到胶带的厚度值,如图6(b)。通过比较薄片厚度的真实值与通过矫正曲线计算得到的薄片厚度值就可验证矫正方法的有效性,实验结果如表2。
仪器的测量精度为0.05 mm,由表2 可知矫正精度高于仪器的测量精度,因而矫正方法是有效的。

图5 高精度钢轨轮廓测量仪Fig.5 High-precision rail profile measuring instrument
4 结束语
本文就如何矫正钢轨磨耗测量的仪器定位偏差进行了研究。提出了一种曲线与曲线偏离程度的衡量方法,该法能有效衡量先后两次测得的曲线之间的偏离度并能方便的进行编程计算。选用了合适有效的模式搜索法实现定位偏差矫正,并验证了其有效性。由于该法是通过拟合由众多离散点构成的曲线来矫正定位偏差,拟合过程中的参考基准多,因而具有很高的矫正精度。矫正精度能满足轮轨动力学研究的要求。本文所述的定位偏差矫正方法也适用于其他领域中类似误差的矫正。
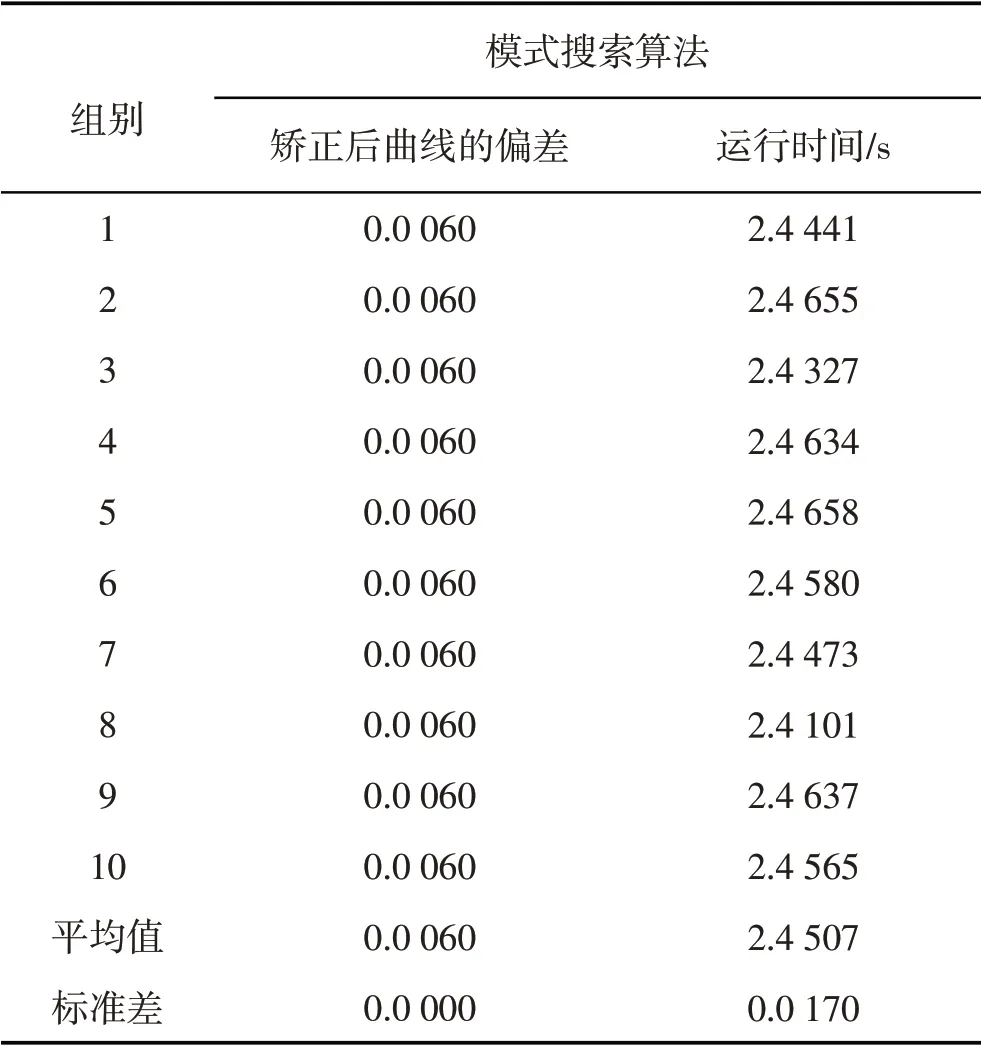
表1 仿真结果Tab.1 The simulation results

图6 测量仪器验证Fig.6 Verification by measuring instrument

表2 仪器验证结果Tab.2 Test results
[1]沈钢,黎冠中,李小江,等.轮轨踏面外形的实际测量及几何接触的进一步研究[J].铁道学报,1999(5):24-28.
[2]周清跃,田常海,张银花,等.高速铁路钢轨打磨关键技术研究[J].中国铁道科学,2012(2):66-70.
[3]程文通.钢轨磨耗测量器测量基准面的选择[J].铁道技术监督,1997(5):32-34.
[4]张为民,朱志浩,樊留群,等.超大构件机加工的定位拟合算法[J].机械工程学报,2006(4):131-134.
[5]陈庄庄,李罡,郑煜.精确对准过程中的算法研究[J].光通信研究,2010(1):66-69.
[6]赵建华,张为民,邱玮.采用模式搜索法对磁悬浮列车轨道梁的加工实现精确定位[J].组合机床与自动化加工术,2007(12):32-34+38.
[7]沈伟杰,沈钢.轮对踏面及轮缘磨耗接触式警报装置研究[J].华东交通大学学报,2013,30(6):40-43+48.
[8]苏勇.一种改进的模式搜索法[J].中小型电机,1997,(3):34-35.
[9]李明.详解MATLAB在最优化计算中的应用[M].北京:电子工业出版社,2011:196-225.
[10]王沫然.MATLAB 与科学计算[M].北京:电子工业出版社,2005:155-162.
