DQ法求解FGM Levinson梁的静态弯曲问题

张静华，魏军扬

（1.扬州大学建筑工程与科学学院，江苏扬州225127；2.中船第九设计研究院工程有限公司，上海200063）

功能梯度材料是一种新型的非均匀复合材料。它是通过特定的材料制备工艺将不同性能的两种或两种以上材料按一定的设计规律组合起来，使材料组分按梯度连续变化，从而达到消除材料的物理性能的不连续性以使内部界面消失。功能梯度材料性能的不均匀性为力学分析带来了很大的困难，许多均匀材料中引入和发展的力学概念、理论、计算方案和实验手段已不再适用于功能梯度材料，需要进行探索和创新［1］。因此，其力学行为研究也成为众多材料科学、物理学和力学工作者非常感兴趣的研究领域，是当前国内外关注的前沿课题。

基于不同的理论，研究者们采用了多种解析和数值方法对功能梯度材料结构的弯曲、屈曲和振动响应进行研究。其中大量的研究成果反映了材料性质的横向梯度变化特性对功能梯度材料梁宏观力学行为的影响。基于经典理论，李世荣和刘平［2］利用解析法研究了材料性质沿横向连续变化的功能梯度Euler-Bernoulli梁的静态弯曲、屈曲和自由振动问题，文献［3］利用DQ法求解了两端简支变截面功能梯度梁的弯曲问题。基于一阶剪切理论，Li［4］引入辅助函数研究了梯度功能材料Timoshenko梁的静态弯曲和横向振动，Li等［5］利用数学模型的相似性和控制方程中载荷的等效性研究了功能梯度Timoshenko梁与均匀Euler-Bernoulli梁静态解之间的相似转换关系，文献［6］采用微分求积法（DQM）分析了层合梁自由振动问题。马连生等［7］研究Euler梁理论、Timoshenko一阶梁理论和Reddy高阶梁理论之间在特征值问题的相关性，将求解微分方程的特征值问题转化为代数方程的求解。基于经典理论和一阶剪切变形理论，文献［8］运用微分求积法（DQM）研究了功能梯度材料矩形板的线性弯曲问题。基于经典板理论，李世荣［9］等采用解析方法研究了轴对称条件下FGM圆板的弯曲、屈曲和自由振动问题，推导出了FGM圆板与对应均匀圆板的挠度、临界载荷和固有频率之间的相似转换关系。利用经典板理论解和一阶剪切变形板理论解之间的对应关系，Reddy等［10］讨论了功能梯度复合材料圆形和环形薄板的对称弯曲问题，推导出了各种边界下FGM圆板轴对称弯曲解析解。基于高阶剪切变形板理论，杨杰，沈惠申［11］采用DQ法和Galerkin法相结合方法研究了在均匀变化的温度场内功能梯度材料矩形中厚板的横向弯曲问题。

1 问题的数学模型

1.1 基本方程

采用高阶剪切变形理论来分析功能梯度材料Levinson梁的静态弯曲问题。考虑长度为l，宽为b高为h的矩形截面功能梯度材料梁，其材料性质沿厚度方向连续变化。设轴向坐标为x，通过横截面的几何形心；横向坐标为z，其原点在几何中面（见图1）。梁的位移场可表示为

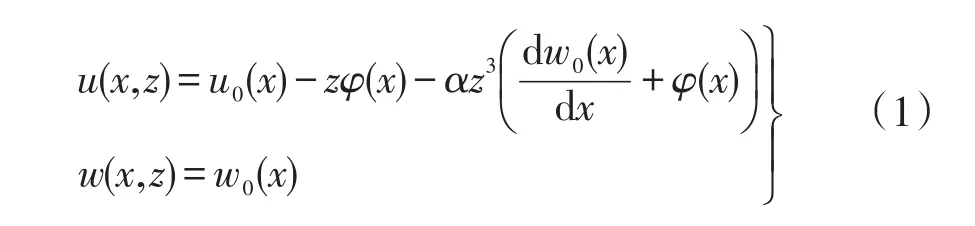
其中：u0(x)为几何中面内任一点的轴向位移；w0(x)为挠度位移；u(x，z)和w(x，z)分别为梁内任一点的轴向位移和竖向位移；φ为横截面转角，系数α=4/(3h2)。对于材料性质横向非均匀变化的功能梯度材料梁，由于梁的几何中面与物理中面不重合，因而几何中面面内位移u0一般不为0。

根据梁的位移方程，即式（1）推出梁的应变场为

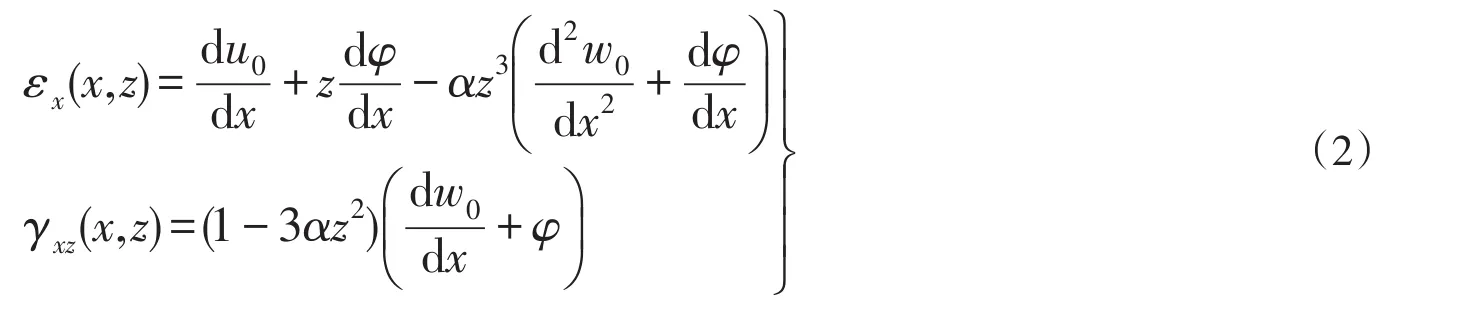
图1 功能梯度梁的几何描述Fig.1 The geometric description of functionally graded beams

式中：εx(x，z)和γxz(x，z)分别为梁内任一点的正应变和剪应变。

根据胡克定律，梁横截面上的正应力σx和剪应力τxz的位移形式如下

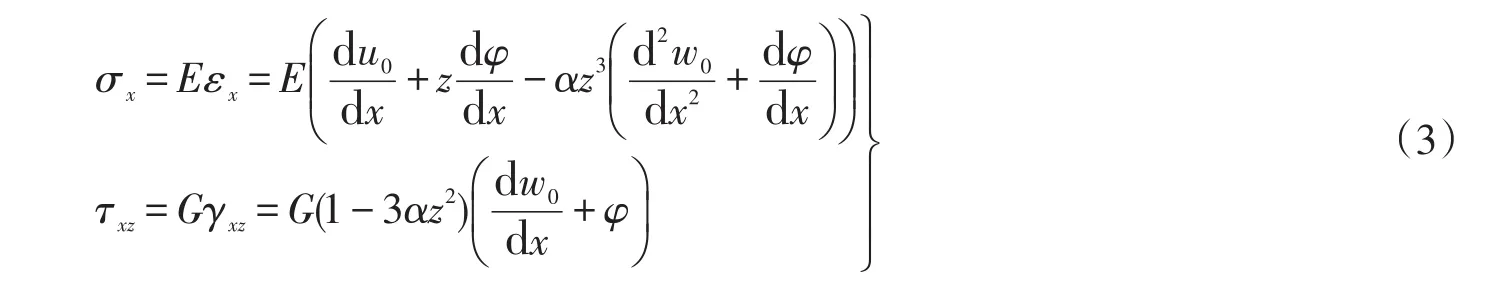
其中：E，G和ν分别为梁的拉伸弹性模量，剪切弹性模量和泊松比，这里假设它们都是横坐标z的已知函数。由式（3）可得梁的横截面等效内力分别为

式中：FN是梁的轴力，M是梁的弯矩，Fs是梁的剪力。其中梁的截面刚度系数定义为

式中：E，v，A分别为梁的弹性模量，泊松比和横截面面积。

考虑梁的微分单元平衡，可得梁的静力平衡方程

其中：q为横向分布载荷。

1.2 材料性质变化规律

考虑梁的材料性质沿厚度方向按幂函数变化，其弹性模量可表示为

其中：-h/2≤z≤h/2；Et=E(h/2)，Eb=E(-h/2)分别为梁的上、下表面的弹性模量；梯度指数p为非负实数。定义梁的无量纲刚度系数为

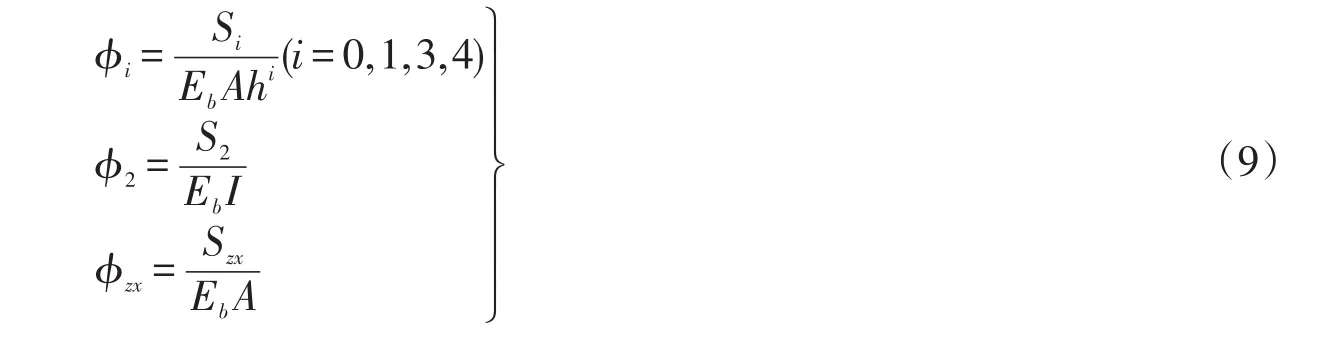
其中：A=bh为均匀梁的横截面面积，I=bh3/12是均匀梁的横截面刚度。将（9）式代入式（7）中，并令η=K-1，K=Eb/Et，积分可得

1.3 无量纲控制方程

采用无量纲变换

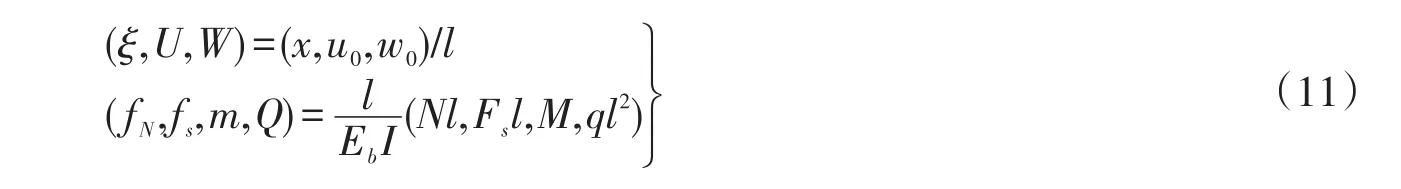
其中：ξ是轴向坐标为x的无量纲化，范围0≤ξ≤1；U和W分别是梁内任一点的无量纲轴向位移和无量纲竖向位移；Q是作用在梁上的无量纲横向分布载荷；fN为梁的无量纲轴力；fs为梁的无量纲剪力；m为梁的无量纲弯矩。

将（4）～（5）式代入（7）式并利用（9）式和（11）式推出无量纲位移形式的控制方程

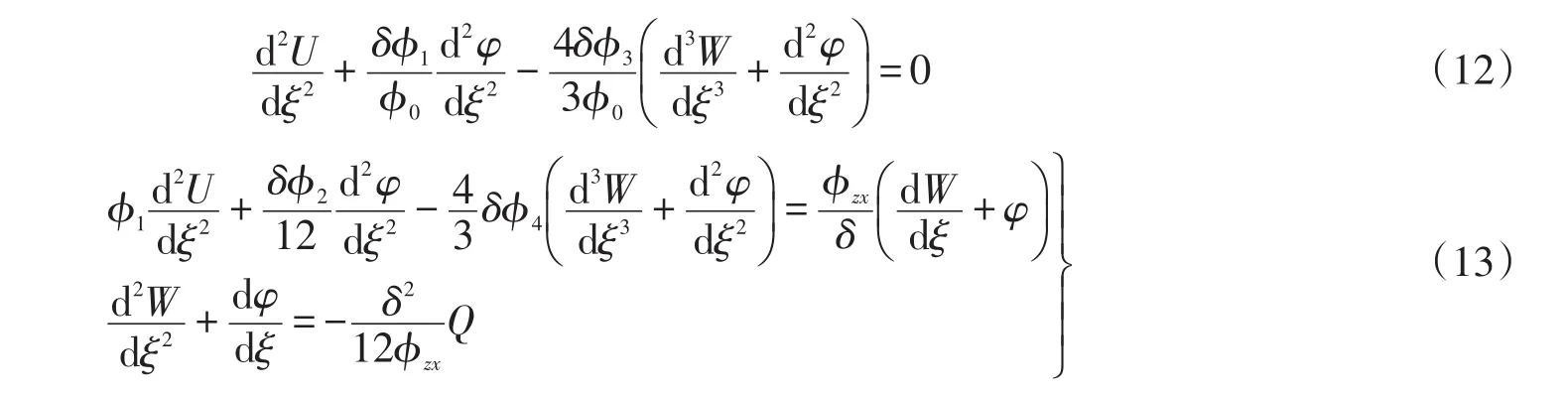
其中：δ=h/l是梁的细长比。

1.4 无量纲内力及边界条件

将（9）式代入（4）～（5）式并利用（11）式推出梁的无量纲位移形式内力

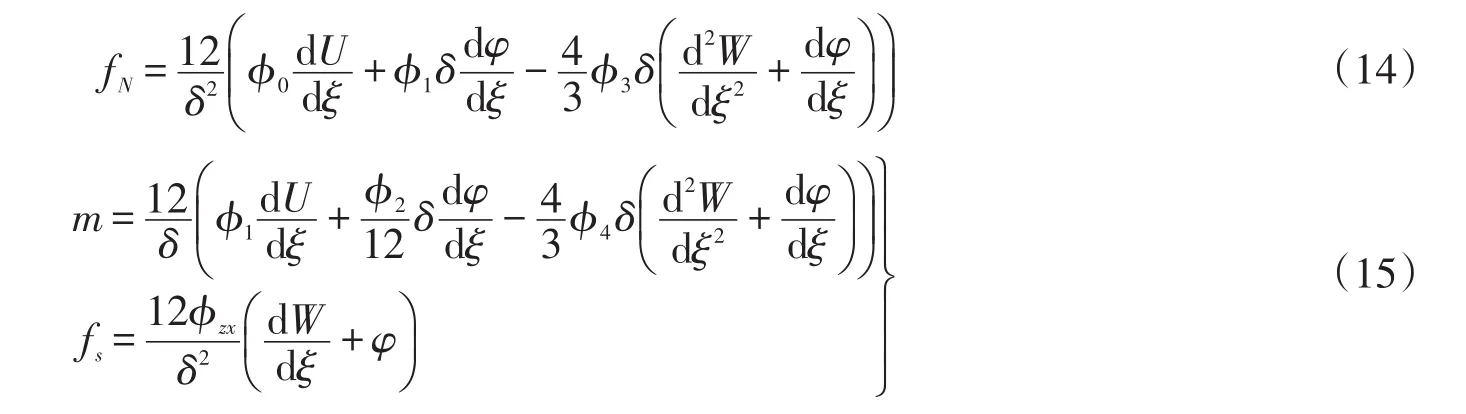
1）两端简支功能梯度Levinson梁的边界条件为

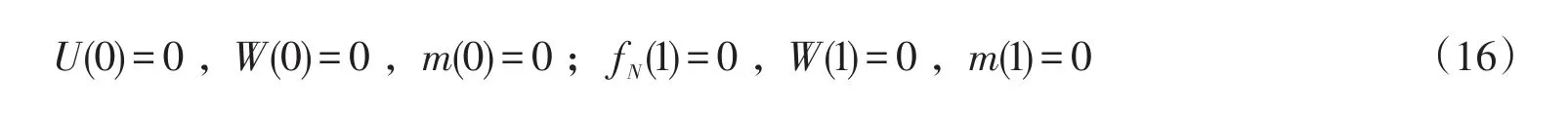
2）一端固定、一端可移夹紧功能梯度Levinson梁的边界条件为：

3）一端固定、一端自由功能梯度Levinson梁的边界条件为：

2 数值计算

2.1 离散方程和边界条件

采用DQ法对上述高阶微分方程进行数值求解。设区间［0，1］上有N个互不重合的结点0=ξ1＜ξ2＜ξ3＜…＜ξN=1，采用非均匀结点划分公式

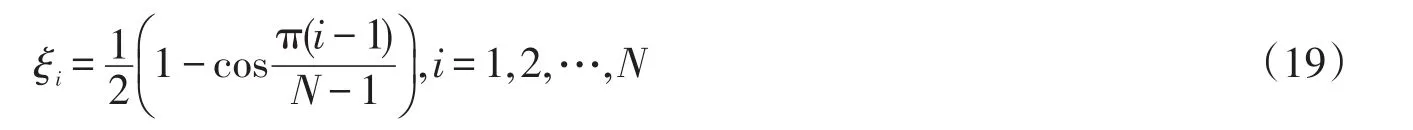
离散后的全部结点位移表示为

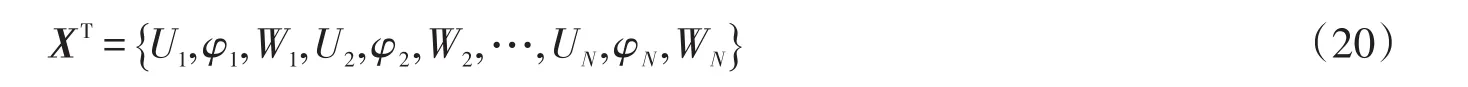
根据微分求积法的基本理论［3］

二阶以及二阶以上权系数可以通过一阶导数的权系数计算获得

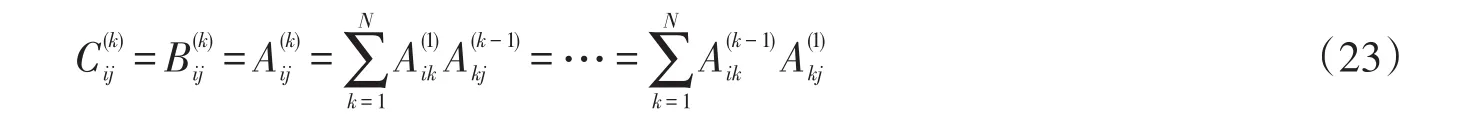
离散后的无量纲控制方程为

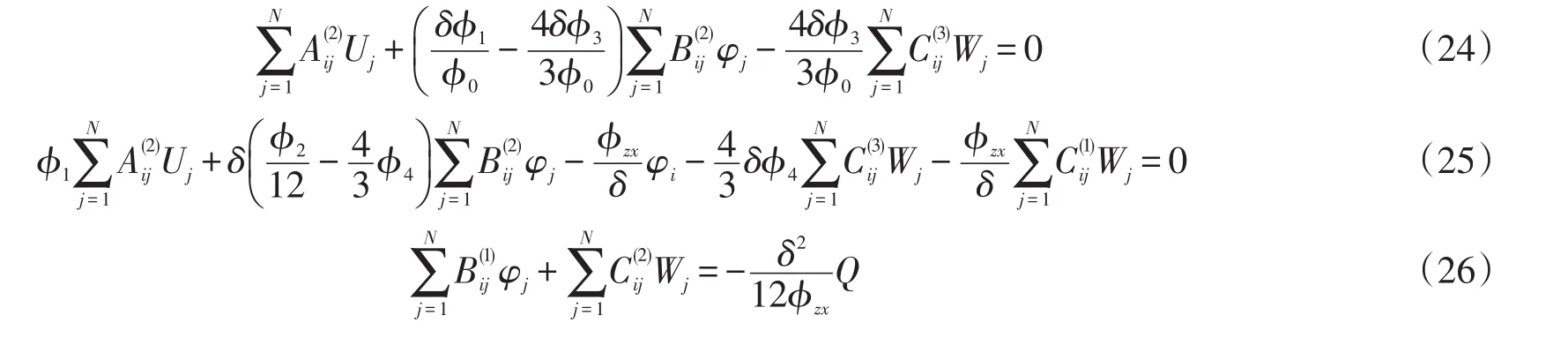
式中：i=1，2，3，…，N。离散后的边界条件分别为

1）两端简支功能梯度材料Levinson梁的边界条件为

2）一端固定、一端可移夹紧功能梯度材料Levinson梁的边界条件为

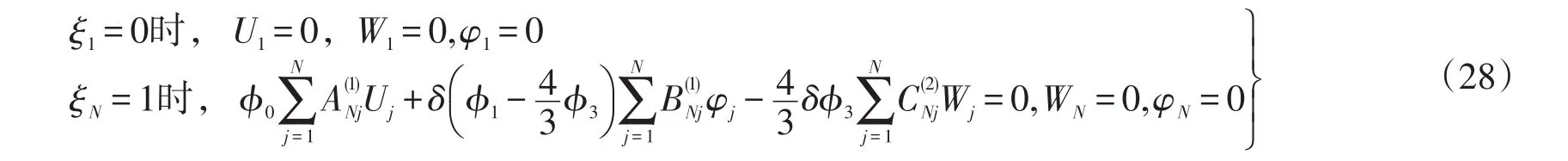
3）一端固定、一端自由功能梯度材料Levinson梁的边界条件为

2.2 算例

给定均布载荷Q=1，具体考虑由陶瓷和金属铝两种组分材料按式（8）所描述的材料性质分布规律构成的功能梯度材料Levinson梁。材料常数分别为Em=70GPa，Ec=380GPa，泊松比v=0.23。表1～4给出了长细比分别为3，5，10和20时，两端简支和一端固定、一端可移夹紧边界条件下功能梯度材料Timoshenko梁的解析解和DQ法计算出的对应的功能梯度材料Levinson梁的无量纲中点挠度随梯度指数p的变化规律，表2～5中第一行是文献［5］中功能梯度材料Timoshenko梁解析解的结果（由文献［5］中式（22）在不同的边界条件下的无量纲中点挠度计算得来，其中横向非均匀系数，无量纲系数

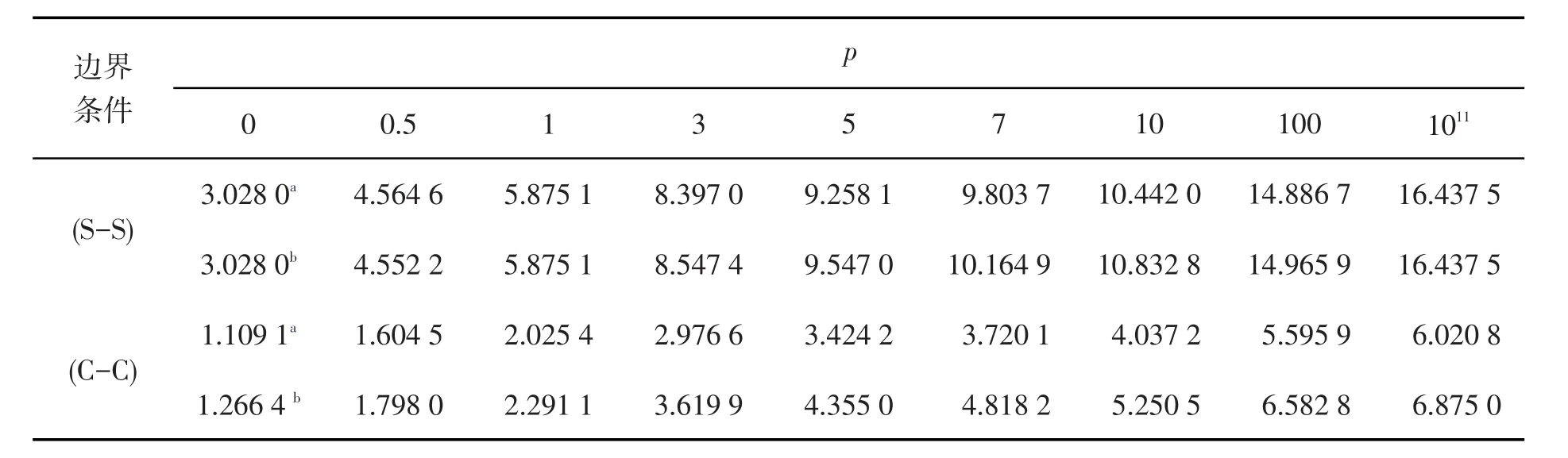
表1 不同边界条件下功能梯度材料Levinson梁的无量纲中点挠度W×103(Q=1，δ=h/l=1/3)Tab.1 Non-dimensional central deflection of functionally graded Levinson beamsunder different boundary conditions W×103(Q=1，δ=h/l=1/3)

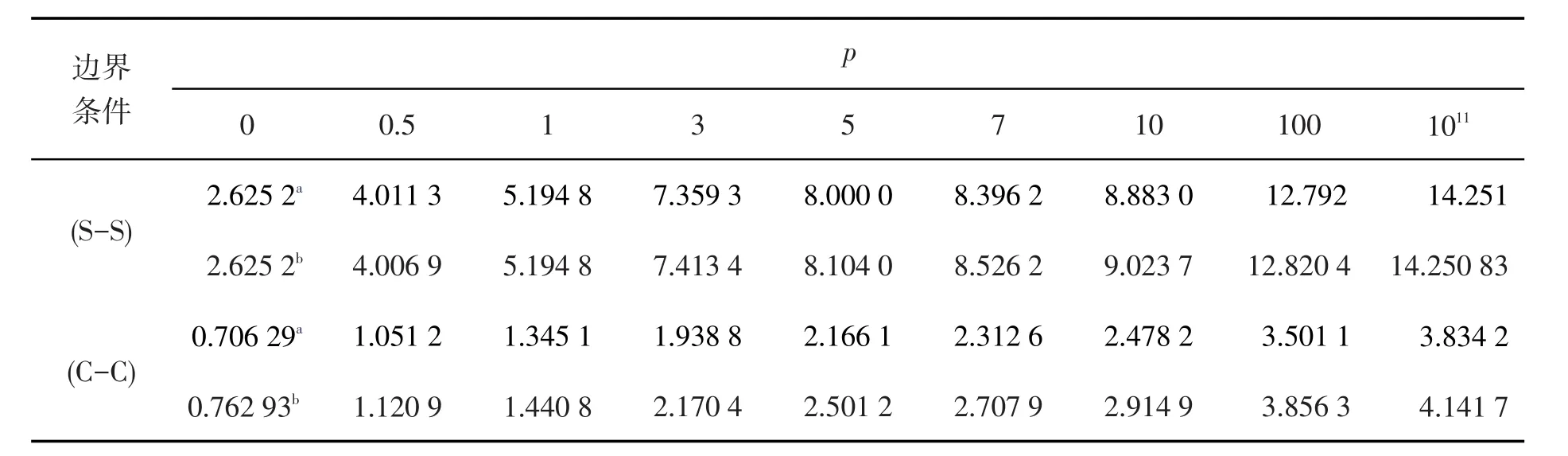
表2 不同边界条件下功能梯度材料Levinson梁的无量纲中点挠度W×103()Q=1，δ=h/l=1/5Tab.2 Non-dimensional central deflection of functionally graded Levinson beams under different boundary conditions W×103()Q=1，δ=h/l=1/5

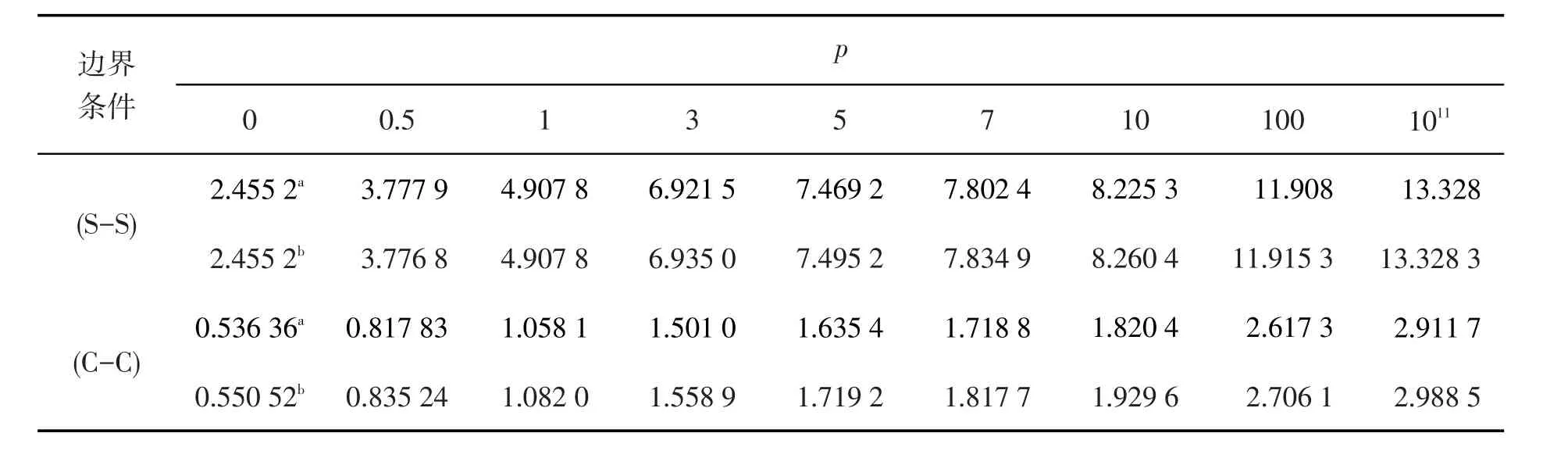
表3 不同边界条件下功能梯度材料Levinson梁的无量纲中点挠度W×103()Q=1，δ=h/l=1/10Tab.3 Non-dimensional central deflection of functionally graded Levinson beams under different boundary conditions W×103()Q=1，δ=h/l=1/10

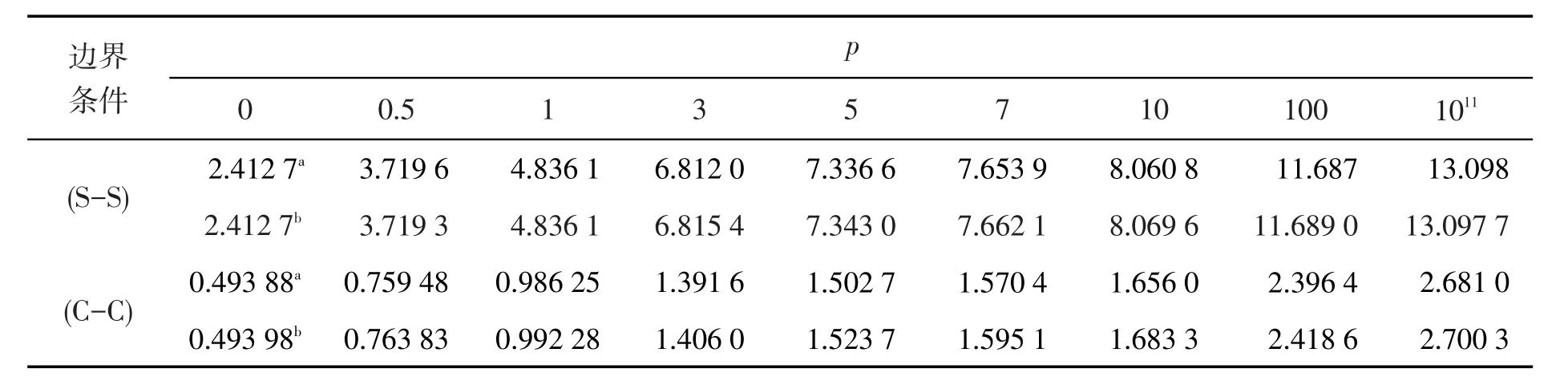
表4 不同边界条件下功能梯度材料Levinson梁的无量纲中点挠度W×103(Q=1，δ=h/l=1/20)Tab.4 Dimensionless deflection parameters of functionally graded beams under different boundary conditions f×103(Q=1，δ=h/l=1/20)

图2描述了均布载荷Q=1，细长比δ=1/10时，不同梯度指数p下两端简支功能梯度材料Levinson梁的挠度曲线，结合表1至表4，得出以下结论：功能梯度材料Levinson梁的最大无量纲挠度都随着梯度指数p的增大而增大，当梯度指数p≥100时，表中挠度的变化已经变得缓慢并逐渐趋向于一个特定的值，这是由于当梯度指数p=0或p→∞时分别对应弹性模量为E≡Eb和E≡Et的均匀材料梁，对于均布载荷Q=1均匀梁的无量纲挠度只与边界条件和长细比有关，在给定的边界条件和长细比下梁的最大无量纲挠度是定值。

图3描述了均布载荷Q=1，梯度指数p=3时，不同细长比下一端固定、一端可移夹紧的功能梯度材料Levinson梁的挠度曲线，结合表1～4，得出以下结论：

1）不同边界条件下，功能梯度材料Levinson梁的无量纲挠度随着细长比δ的增大而增大，当细长比达到δ=1/20时，功能梯度材料Levinson梁和对应功能梯度Timoshenko梁的无量纲挠度几乎相同，这就说明DQ法计算出的对应的功能梯度材料Levinson梁的弯曲挠度是可靠的。

2）随着细长比δ的增大，高阶剪切变形理论下的Levinson梁和一阶剪切变形理论下的Timoshenko梁的无量纲挠度差异也增大，当细长比δ≥1/5时差异开始变得明显，因此计算深梁的挠度时，一阶剪切变形理论不够精确，需要用到高阶剪切变形理论来进行运算。而当细长比δ≤1/10时，一阶和高阶剪切变形理论下的无量纲挠度差异较小，到长细比δ=1/20时，这两种理论下的挠度曲线基本重合。

图2 不同梯度指数下功能梯度Levinson悬臂梁的无量纲挠度曲线W×103()Q=1，δ=h/l=1/10Fig.2 Dimensionless deflection curves of cantilever FGM Levinson beams for differentvaluesof the power law index W×103()Q=1，δ=h/l=1/10

图3 不同细长比下两端简支功能梯度Levinson梁无量纲挠度曲线W×103()Q=1，p=3Fig.3 Dimensionless deflection of S-SFGM Levinson beams for differentslenderness ratio W×103()Q=1，p=3

3 结论

基于高阶剪切变形理论，采用微分求积法（DQM）研究了功能梯度Levinson梁的弯曲问题，得出了以下结论：

1）功能梯度材料Levinson梁的最大无量纲挠度都随着梯度指数p的增大而增大，当梯度指数p≥100时，表中挠度的变化已经变得缓慢并逐渐趋向于一个特定的值。

2）功能梯度材料Levinson梁的无量纲挠度随着细长比δ的增大而增大，当细长比达到δ=1/20时，功能梯度材料Levinson梁和对应功能梯度Timoshenko梁的无量纲挠度几乎相同。

3）随着细长比δ的增大而增大，高阶剪切变形理论下的Levinson梁和一阶剪切变形理论下的Timoshenko梁的无量纲挠度差异也增大，当细长比δ≥1/5时差异开始变得明显，因此计算深梁的挠度时，一阶剪切变形理论不够精确，需要用到高阶剪切变形理论来进行运算。

[1] 仲政，吴林志，陈伟球.功能梯度材料与结构的若干力学问题研究进展[J].力学进展，2010，40(5):528-541.

[2] 李世荣，刘平.功能梯度梁与均匀梁静动态解间的相似转换[J].力学与实践，2010，32(5):45-49.

[3] 张靖华，龚云，李世荣.微分求积法求解变截面功能梯度梁的弯曲问题[J].甘肃科学学报，2010，22(1):14-17.

[4] Li X F.A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams[J].Journalof Sound and Vibration，2008，318:1210-1229.

[5] SHIRONG LI，DAFU CAO，ZEQINGWAN.Bending solutions of FGM timoshenko beams from those of the homogenous Euler-Bernoullibeams[J].Applied MathematicalModelling，2013，37:7077-7085

[6] 宋丽红，陈殿云，张传敏.层合梁自由振动的微分求积分析[J].河南科技大学学报:自然科学版，2005，26(2):89-92.

[7] 马连生，欧志英，黄达文.不同梁理论之间简支梁特征值的解析关系[J].工程力学，2006，23(10):91-95

[8] 付俊强.邓春志DQ法求解功能梯度矩形板的弯曲问题[J].西华大学学报:自然科学版，2011，30(5):38-42.

[9] 李世荣，高颖，张靖华.功能梯度均匀圆板静动态解之间的相似转换关系[J].固体力学学报，2011，32(S1):120-125.

[10] REDDY JN，WANG CM，KITIPOMCHAIS.Axisymmetric bending of functionally graded circular plates[J].European Journal ofMechanics-A/Solids，1999，18:185-199.

[11] 杨杰，沈惠申.热/机械载荷下功能梯度材料矩形厚板的弯曲行为[J].固体力学学报，2003，24(1):119-124.