基于收益最大化的电动汽车充电站选址规划

宋志成，王 勋，伦 利，陈首昆

（华东交通大学电气与电子工程学院，江西南昌330013）

大气中二氧化碳（CO2）浓度伴随化石能源的使用不断升高，全球变暖也给人类的生存和发展带来了严峻的挑战。据统计交通行业的温室气体的排放量占总排量的25%，能源消耗占总能源消耗的40%。［1］电汽车具有高效、节能、能源利用率高、零排放等优点，受到世界关注。我国科技部《电动汽车科技发展“十二五”专项规划》也将电动汽车确定为未来汽车产业主要发展方向［2-3］。电动汽车充电站作为电汽车发展的配套基本设施，其布局规划受到了城市规划部门、交通部门和供电等部门高度关注，因此电动汽车充电站最优规划成为了一个值得研究的重要问题。

针对此问题，文献［4-9］主要研究了电动汽车充电站的建设成本对其选址规划的影响，其中重点考虑建设费用包括基本设备费用、线路改造费用、运行成本、维护成本、土地征用费用。其中文献［4］侧重考虑了电动汽车数量增长、充电站服务范围、充电需求分布、城市规划等因素，最后通过成都市充电站布局规划算例验证；文献［5］中通过对一区域的交通流量信息进行分析，来确定建设充电站的位置和充电站的规模。文献［6］中设定某区域电动汽车容量一定，建立一个充电站的初始建设成本和运行成本最小数学模型。

本文提出了充电站最大收益作为充电站选址目标，其不仅考虑了车站的建设成本和运行成本，而且把电动汽车分布作为了一个很重要的影响因子。算例分析表明，通过考虑电动汽车分布情况，可以有效的减少充电消耗成本，提出的收益最大化数学模型可以很好的解决此选择优化问题。

1 电动汽车充电站规划的数学模型

充电站的主要功能是向各类电动汽车用户提供快速、高质量的电能供应服务，其建设需要综合考虑充电汽车数量、类型、征地费用、运行费用等因素。本文以投运至目标年充电站收益最大化为目标，考虑充电站的建设、运行等成本，区域电动汽车数量情况为约束条件，建立综合优化数学模型。

1.1 目标函数

式中：Smax表示充电站年均收益最大化，Czy为电动汽车的年总营业额，Cjs为充电站的年均建设成本，Cyx为充电站的年均运行成本，Cxh为电动汽车到充电站年均消耗的成本。

1）充电站年总营业额

式中：ε为电动汽车每次充电费用；ρ为每辆电动汽车每年充电次数；Qcari为到i充电站充电的电动汽车数量。

2）充电站年均建设成本

年均建设成本主要由固定成本费用和征地费用组成。其中固定成本包括基础设施费用（充电机、变压器、控制器等电气设备）和基础设施建设费用，根据北京市出台的《电动汽车电能供给与保障技术规范：充电站》标准文件可推算出多等级充电站的固定费用。因此年均建设运行成本可表示为：

式中：r为充电站成本回收率；k为投资回收年限；n为充电站建设个数；为第i个充电站所占面积；为第i个充电站建设位置的征地单价；为第i个充电站基本设施的建设费用。

3）充电站年均运行成本

充电站的运行成本主要包括充电站购电费用和人工工资、设备维护费用，故充电站年均运行成本模型为：

式中：α为电动汽车充电费用的购电率；β为人员工资、设备维护费用等费用折算为充电站年收入的系数。

4）电动汽车充电年消耗成本

该式表示电动汽车到与其最近充电站所消耗的成本的总和，式中：M为电动汽车聚合点的个数；ω表示电动汽车的距离消耗参数；rij表示j号电动汽车聚合点离其最近充电站i的距离；Qj为电动汽j号电动汽车聚合点的电动汽车数量。

4）区域电动汽车数量

该式表示i充电站所服务区域的电动汽车总数，式中：m表示该充电站服务区域电动汽车聚合点的个数；Qj为第j号电动汽车聚合点电动汽车的数量。

根据式（1）～（5）可得出目标函数：

1.2 约束条件

式（8），（9）为约束条件，表示充电站应满足区域服务半径的要求以及最大充电要求，rij为j功能区到i充电站的距离；rmax为充电站最大的服务半径；γmax为最大同时充电率，Zj为区域充电站的充电机个数。

2 微分进化算法

1995年～1997年Storn和Price提出的微分进化算法，该算法与PSO算法从表上看非常相似，但其还具备了一些遗传算法的特征，所以可以把其称为PSO与遗传算法的结合。微分进化算法（DE，differential evolution），其具有收敛速度快、可调参数少、算法简单、鲁棒性好等特点，现逐渐受到了大家关注和热捧。该算法与免疫算法、遗传算法等进化算法一样，主要分为初始化、差分变异、交叉、保优选择这几个基本步骤［10-13］。

2.1 初始化

DE算法和遗传、粒子群等算法一样，需要生成初始种群和个体。一般情况下，初始种群会从给定的范围内随机选择，覆盖整个参数空间。设种群规模为NP，其第i个体Xi=(xi,1,xi,2,···xi,n)，n为问题解空间的维数，初始种群s={X1,X2,···XNP} ，Xi∈Rn为个体的集合。个体一般按下式生成：

式中：xi,j为Xi的第j个分量，xi,jmax、xi,jmin为为Xi的第j个分量的上下限。

2.2 变异

微分进化的策略有很多种，本文以DE/rand/1策略进行变异处理。从第k代个体随机选取三个不同的个体r1、r2、r3，根据变异策略生成第k+1 代变异中间个体。变异策略式中的F为放缩因子，其取值范围为（0，1）。

2.3 交叉

为满足参数向量的多样性，在变异操作结束后，对目标向量与其他变异向量进行交叉操作。交叉操作规则如下：

式中：ηj∈（0,1）为针对第j维分量随机选取的控制参数；为CR∈（0,1）为交叉因子；qj为从[1，Np]中随机选取的一个整数，其确保了交叉至少有一分量。

2.4 选择

接着进入选择操作，选择以下公式进行选择：

如果目标向量值超过了设定值域，该参数将在设定值域内重新随机生成，然后计算目标向量适应度，与本式的适应度相比较，将最优的适应度值取代当前值。

2.5 算法基本思想

首先针对问题需求设计个体表示形式，然后初始化种群规模NP、缩放因子F、交叉常数CR及最大迭代次数Nmax等DE参数。其中比例因数F和交叉因数CR在进化过程中的取值区间一般分别是（0.4，0.9）和（0.3，0.8），它们的优化值往往依赖于目标函数的特性。算法流程如图1所示。

3 算例研究

为了简化模型求解，现假设一个面积为36 km2经济开发区，把其分割成16 个功能区（商业、工业、居民），如图2所示。预计至2020年改开发区人口总计10.61万人，该区百人汽车保有量将达到9辆，电动汽车市场份额为50%，各小区电动汽车的位置和数量如表1所示。

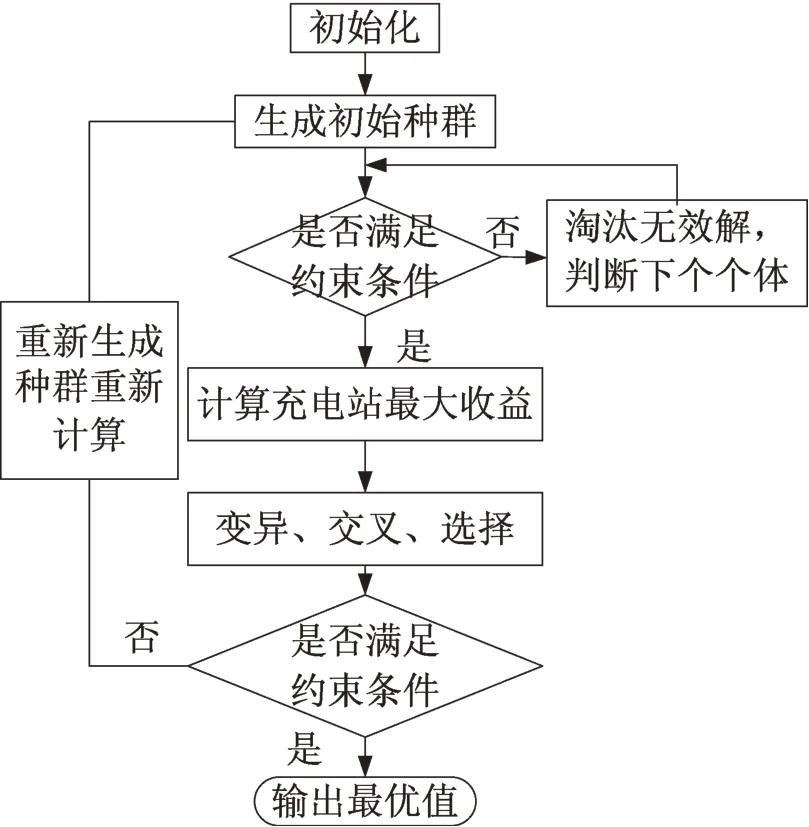
图1 微分算法流程图Fig.1 Flow chart of differential algorithm

图2 电动汽车位置分布图Fig.2 Location map of electric vehicles

表1 电动汽车数量及位置Tab.1 Number and location of electric vehicles

由表1可知，在该区域有4776辆电动汽车，根据公式（9）推算该区域最少要建设4台以上的充电站才能满足该区的充电需求。根据表2、3、4中的数据，结合本文所建设最大收益数学模型。现分别以充电站个数n（4～15）为循环变量，分别计算出充电站数为n时的最大收益和规划结果。

表2 充电站的等级及相应的建设成本Tab.2 Station levels and the corresponding construction costs

表3 各类型的征地成本Tab.3 Costs of different lands

表4 参数取值Tab.4 Parameter settings

算法参数的选取为：种群数量为30；限定迭代次数200次；比例因子为0.85；交叉因子为0.5。对该假设的算例独立运行40次，计算出4-15坐充电站的最大收益分别为636，651，634，597，562，547，505，470，424，383，318和277万元。可知，在此给定的条件下在该开发区建设4座或6座充电站收益较大，建设5座充电站为最优。从计算结果可以看出，随着充电站建设数量逐渐增加，其成本不断上升，最终导致其收益逐渐减少，此结果符合预期设想。规划建设的5座充电站的坐标和等级如图所示。

图2 选址优化最优计算结果Fig.2 Optimal planning results of charging stations

5 结束

本文以整个区域充电站综合最大收益为目标，该目标函数考虑了建设充电站的土地成本和变压器、充电机等固定设备成本，同时考虑了工人工资等运行成本。通过微分进化算法，对某假定区域电动汽车充电站进行了规划，得出如下结果：

1）本文提出的数学模型，其不仅考虑了建设充电站的建设费用、充电站的运行费用和电动汽车分布情况对充电站选址的影响，而且把充电站用地的价格和充电站的规模对选址影响考虑在内，比较科学、全面地反应了电动汽车充电站选址问题。

2）通过对算例的计算与分析，可知本文所构建的目标函数是科学、可行的。

［1］王贺礼，谢运生，罗成龙等.交通运输业温室气体排放现状及减排对策［J］.能源研究与管理，2011（3）：11-13.

［2］吴憩棠.解读《电动汽车科技发展“十二五”专项规划》（摘要）［J］.汽车与配件，2012（15）：12-15.

［3］电动汽车科技发展“十二五”专项规划（摘要）［N］.科技日报，2012-03-03（004）

［4］刘自发，张伟，王泽黎. 基于量子粒子群优化算法的城市电动汽车充电站优化布局［J］. 中国电机工程学报，2012，32（22）：39-45.

［5］刘志鹏，文福拴，薛禹胜等.电动汽车充电站的最优选址和定容［J］.电力系统自动化，2012，36（3）：54-59.

［6］唐现刚，刘俊勇，刘友波等.基于计算几何方法的电动汽车充电站规划［J］.电力系统自动化，2012，36（08）：24-30.

［7］PUTRUS G A，SUWANAPINGKARL P，JOHNSTON D，et al．Impact of electric vehicles on power distribution networks［C］//IEEE Vehicle Power and Propulsion Conference.Michigan：IEEE，2009：827-831.

［8］WANG HENGSONG，HUANG QI，ZHANG CHANGHUA，et al．A novel approach for the layout of electric vehicle charging station［C］//International Conference on Apperceiving Computing and Intelligence Analysis（ICACIA）. Chengdu：University of Electronic Science and Technology of China，2010：64-70.

［9］IP A，FONG S，LIU E．Optimization for allocating BEV recharging stations in urban areas by using hierarchical clustering［C］//6th International Conference on Advanced Information Management and Service（IMS）.Seoul，Korea，2010：460-465.

［10］刘自发，闫景信，张建华，等.基于改进微分进化算法的电力系统无功优化［J］.电网技术，2007，31（18）：68-82.

［11］李国庆，冀瑞芳，张健，等.基于改进微分进化算法的可用输电能力研究［J］.电力系统保护与控制，2011，39（21）：22-27.

［12］彭春华，齐彦伟，陈首昆.基于分层分区模型的分布式电源分布优化［J］.华东交通大学学报，2013，（02）：85-89.

［13］吴骅，吴耀武，娄素华，等.基于改进微分算法的负荷模型参数辨识［J］.高电压技术，2008，34（09）：202-206.