航天器火工分离螺母的火工冲击环境数值仿真研究
2014-12-21刘天雄李长江向树红张庆明
张 欢,刘天雄,李长江,向树红,张庆明
(1.北京空间飞行器总体设计部,北京 100094;2.北京卫星环境工程研究所,北京 100094;3.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引言
火工装置是由作动器、装药和功能机构组成,利用装药燃烧或爆炸产生的载荷通过功能机构来完成特定功能的装置[1]。航天器火工装置在完成连接与释放、切割与破碎、阀门打开与关闭等动作时会产生高量级、宽频带、短时间的复杂爆炸冲击环境,从而对航天器电子仪器、脆性材料、轻薄结构 等产生破坏作用。典型火工冲击故障模式包括晶体、陶瓷、环氧材料、玻璃封装材料、焊点、电缆引线头等的破裂、密封失效、污染粒子扩散、继电器和开关的抖动及切换、微电子芯片结构变形等[2-3]。
火工分离螺母用于卫星与运载火箭上面级的连接。本文使用LS-DYNA 程序对火工分离螺母分离过程开展数值仿真分析,重点关注分离螺母解锁时序的正确性、应力波在结构材料中的传播过程以及关键位置的结构加速度响应和载荷输出,以便对该螺母的试验结果做出预示。该仿真可作为提高火工分离螺母可靠性和开展优化设计等工作的参考,其仿真结果可为航天器抗火工冲击防护设计提供更加真实的载荷输入,对缩短设计周期、提高分离方案有效性有重要意义。
1 数值仿真模拟算法
1.1 有限元控制方程
在动力学有限元分析中,系统的控制方程可描述为[2]

式中:M为总质量矩阵;C为阻尼系数矩阵;K为总刚度矩阵;f为节点载荷向量。
在显式动力学理论中,通常采用直接积分法中的中心差分格式对运动控制方程进行积分。在中心差分格式中的加速度和速度可用位移表示为

式中:ut是t时刻的位移;ut-Δt是t-Δt时刻的位移;ut+Δt是t+Δt时刻的位移。将式(2)和式(3)代入式(1)可得用于求解各个离散时间点的位移的递推公式:

在此递推算法中存在一个起步问题,当t=0时,为了计算uΔt,除了初始条件u0已知外,还需要知道u-Δt。由式(2)、式(3)可得

式中,(0)u˙ 可以从给定的初始条件中得到,而 (0)u˙ 则可以利用t=0 时的式(1)得到。
应该注意到中心差分格式是条件稳定算法,即增量步长Δt必须小于某个临界值Δtcr,否则算法将是不稳定的。中心差分格式的解的稳定性条件是[3]

式中Tn为有限元系统的最小固有振动周期。
1.2 算法选择
LS-DYNA 以Lagrange 算法为主,兼有Euler和ALE(Arbitrary Lagrange Eulerian)算法[4-5]。作为LS-DYNA的主要算法,Lagrange算法用Lagrange坐标系来描述物体变形,点的坐标固结在变形体的内部,并跟踪质点的运动,它的质量自动守恒,能够清晰地显示求解区域内部多种物质的界面和自由界面,明确地定义及直观地处理边界条件;但对于大变形情况,网格可能发生严重畸变而导致计算终止。Euler 算法用Euler 坐标系描述物体运动,坐标系固定在空间里,当物体运动变形时,坐标系不变,适用于描述材料有大扭曲变形的问题,然而它不显式地描述接触面和材料边界,因此对各类固体边界和接触面的定义很不方便,也不便于描述复杂的材料本构关系。ALE 算法是为解决流体问题而在吸收Lagrange 算法和Euler 算法的基础上发展起来的一种混合算法,它可以克服单元严重畸变引起的数值计算困难,很好地处理整个物体发生空间位移及本身发生大变形的问题,并实现流-固耦合的动态分析。由于火工分离螺母包含火工单元,若采用Lagrange 网格,炸药及空气在数值模拟的过程中会产生大的变形,畸变的网格可能会减慢运算速度甚至会导致计算终止[4-7],所以本文对空气及炸药采用ALE 网格,螺栓等其他结构采用Lagrange 网格,并采用*CONSTRAINED_LAGRANGE_IN_SOLID 工具完成ALE 与Lagrange 网格的耦合。
1.3 材料本构及状态方程
火工分离螺母采用带失效模式的塑性随动模型[4],弹塑性材料模型包括随动硬化、各向同性硬化及其组合硬化3 种模式,硬化模式由硬化参数β(0≤β≤1)控制,当β=0 时材料为随动硬化,β=1时则为各向同性硬化,0<β<1 时为混合硬化。控制关键字为*MAT_PLASTIC_KINEMATIC,输入数据主要包括:密度ρ,弹性模量E,泊松比υ,初始屈服极限σ0,切线模量ET。材料参数见表1。

表1 火工分离螺母的拉格朗日域材料参数[4]Table 1 Material parameters of Lagrange region for pyroshock separation nut
1.3.1 线性状态方程
空气采用空白材料模型,用线性状态方程描述,材料参数见表2[4]。
线性多项式状态方程为:Pa=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E,其中:Pa为空气压力;E为单位体积内能;μ=ρ/ρ0- 1,ρ为当前气体密度,ρ0为初始空气密度;C0~C6是状态方程参数,对于空气,C0=C1=C2=C3=C6=0,C4=C5=γ-1,γ是比热系数。

表2 空气材料模型的状态方程参数Table 2 Parameters of material and state equation of air
1.3.2 爆轰产物状态方程
火工品采用高能炸药燃烧材料模型,由JWL状态方程描述。
爆轰产物状态方程是炸药爆轰C-J 状态之后,爆轰产物系统中各物理量(压力、体积、温度等)之间的关系式,它体现了炸药的做功能力。LS-DYNA 中凝聚炸药及爆轰产物材料模型采用了JWL 状态方程,控制关键字为*EOS_JWL。JWL状态方程的形式为

式中:P为爆轰产物的压力;V是相对比容,V=v/v0,量纲为1,v= 1/ρ是比容,v0是初始比容;e是比内能,可由炸药的绝对内能es和初始比内能e0得出,es=mCVT,e0=es/v0=ρ0mCVT,e=es/v=e0/V;A、B、R1、R2、ω这5 个常数需通过试验数据拟合,当炸药密度大于1 g/cm3时,可通过γ拟合法,而不需做试验。
本文采用的材料参数见表3。

表3 火工品材料C-J 参数及JWL 状态方程参数[8]Table 3 Parameters of material C-J and JWL state equation of detonater
1.4 预紧力的施加
根据文献[9],拧紧力矩T与轴向预紧力p的换算公式分别为

式中:K是拧紧力矩系数,一般取0.2;d是螺栓直径;F0是轴向力;S是螺栓截面积。本模型中,T= 70 N·m,d= 0.012 m。经计算p= 258 020 759 Pa。
使用如图1的预紧力载荷曲线,施加位置为螺栓中部截面。该曲线使预紧力得到缓慢施加而不产生明显的应力波效应,脉宽的选取为计算开始至预紧力开始释放的时间。

图1 预紧力曲线Fig.1 Initial stress curve
1.5 接触类型选择
使用*CONTACT_SURFACE_TO_SURFACE 工具定义零件间的接触,同时使用*CONTACT_ INTERIOR 关键字定义Lagrange 域网格的自体接触,这样定义的接触可以降低因连续的两层单元出现负体积而使计算停止的概率,使动力松弛部分预紧力的计算更加稳定。
2 有限元模型建立
仿真分两步进行:先建立分离螺母模型,实现螺母的正确解锁;然后建立分离螺母与星箭接口局部结构组装模型,并输出星箭界面载荷,为卫星的防护设计提供载荷输入。
2.1 火工分离螺母有限元模型
采用TRUEGRID 和LS-PREPOST 软件作为前处理软件,Lagrange网格均采用SOLID实体单元,ALE 网格采用SOLID_ALE 单点多物质单元。单元尺寸最小0.02 cm,最大0.1 cm,单元总数454 619。划分好的有限元模型剖面图见图2。

图2 火工分离螺母有限元模型剖面图Fig.2 Sections of pyroshock separation nut FEA mode
2.2 火工分离螺母-航天器结构一体化建模
火工分离螺母和航天器结构的组合体模型见图3,其中卫星接头采用SOLID 单元,运载火箭上面级为实体SOLID 单元加SHELL 壳单元,SHELL 厚度为2 mm,连接界面采用共节点。计算时提取典型位置A1、A2、A3 的加速度响应数据。
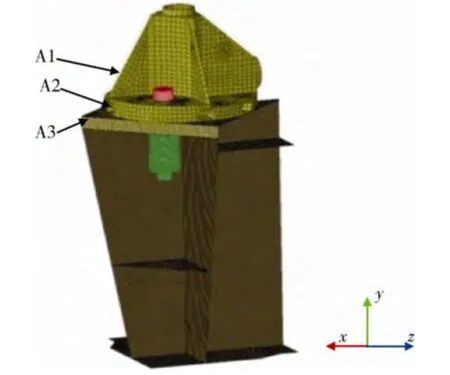
图3 火工分离螺母-航天器结构一体化模型Fig.3 Integration FEA model of pyroshock separation nut and spacecraft structure
3 计算结果与分析
3.1 动态解锁过程
火工分离螺母的解锁过程见图4,解锁过程按正确的工作时序完成,在做功元件活塞的推动作用下锁紧瓣发生较大变形。

图4 火工分离螺母的动态解锁过程Fig.4 Dynamic separation process of pyroshock separation nut
3.2 火工品爆炸过程
图5和图6显示了应力波在卫星接头和运载火箭上面级的传播过程,这一过程在100 µs 左右开始,“波”的形状已不太明显,这主要是由应力波 过界面后的反射、折射和衍射引起的。因为卫星接头的刚度比运载上面级的刚度大,所以应力波在卫星接头中的传播更快,应力波过界面后迅速衰减。

图5 卫星接头上的应力波传播Fig.5 Stress wave propagation in satellite tie-in material

图6 运载上面级上的应力波传播Fig.6 Stress wave propagation in upper stage of launch vehicle
提取结构靠近分离螺母近场典型位置的加速度响应曲线(见图7)可看出:在1 ms 内按照爆炸、预紧力释放、结构撞击的时序出现了3 个峰值,其中爆炸过程峰值明显,并且很快衰减;预紧力释放过程的峰值最大,能量释放最多;碰撞过程的峰值不明显,能量释放较少,与产品手册中提供的数据一致。

图7 近场典型位置的加速度响应Fig.7 Acceleration response at typical position in near field
3.3 组合体计算结果
典型位置A2 的y向加速度响应曲线(见图8),与试验1 ms 数据对比,加速度响应与试验数据量级相同,且按照解锁过程爆炸、预紧力释放及结构撞击的时序出现了3 个峰值,与试验情况相符。

图8 典型位置A2 的y 向加速度响应Fig.8 y direction acceleration response at typical position A2
提取了星箭界面卫星接头一侧的载荷曲线(见图9~图11),可以看出:x向和z向的载荷曲线相似,均为沿时间轴上下振荡;y向载荷有3 个较大的离散峰值,曲线在时间轴一侧,其值均为正。3个曲线可作为星箭接口结构火工冲击响应预示的输入条件。

图9 星箭界面x 向界面力Fig.9 x orientation load of satellite and launch vehicle interface

图10 星箭界面y 向界面力Fig.10 y orientation load of satellite and launch vehicle interface

图11 星箭界面z 向界面力Fig.11 z orientation load of satellite and launch vehicle interface
3.4 结构加速度响应预示
以星箭界面提取的力曲线作为载荷输入,通过MPC 将星箭界面节点与一个节点连接,在该点施加3 向载荷,以NASTRAN SOL112 SOLVER 为求解器,对图3中典型位置A1、A2、A3 的y向结构加速度响应进行预示,并与试验结果进行对比(如图12~图14所示),可以看出,典型位置的结构加速度冲击响应与试验值基本吻合。预示结果满足制定组件冲击试验条件的要求,火工分离螺母动作时产生的瞬态冲击载荷可以作为火工冲击防护设计的载荷输入。

图12 A1 位置y 向的加速度响应与试验值对比Fig.12 Comparison between calculation and test data of acceleration response in y direction at position A1

图13 A2 位置y 向的加速度响应与试验值对比Fig.13 Comparison between calculation and test data of acceleration response in y direction at position A2

图14 A3 位置y 向的加速度响应与试验值对比Fig.14 Comparison between calculation and test data of acceleration response in y direction at position A3
4 结论
本文使用LS-DYNA对火工分离螺母的动态分离过程进行了数值仿真,根据仿真结果,得到以下主要结论:
1)LS-DYNA 软件能够很好地模拟火工分离螺母的动作,准确反映火工品爆炸、预紧力释放及零件结构撞击过程。应力波在刚度大的结构材料中传播更快,过界面后迅速产生衰减。此传播信息可以作为冲击环境防护设计的参考。
2)关键点的加速度响应随动作时序产生离散的峰值,火工品爆炸、结构预紧力释放及零件结构撞击时将分别产生加速度响应峰值。螺栓结构预紧力释放过程引起的结构加速度响应峰值大于爆炸应力波传播引起的结构加速度响应峰值。结构撞击引起的加速度响应峰值与应力波引起的结构响应峰值相当。
3)火工分离螺母-航天器结构一体化建模所提取的界面力曲线可以作为火工冲击防护设计的载荷输入;本文使用的数值仿真方法可用于航天器结构响应预示。
(References)
[1]张欢, 刘天雄, 李长江, 等.航天器火工冲击环境防护技术现状与应用[J].航天器工程, 2014, 23(2):104-113 Zhang Huan, Liu Tianxiong, Li Changjiang, et al.Status and application analysis of spacecraft pyroshock protecting techniques[J].Spacecraft Engineering, 2014, 23(2):104-113
[2]周杰梁, 郑百林.基于中心差分法的纤维结构碰撞动力学分析[J].力学季刊, 2011, 32(3):466-472 Zhou Jieliang, Zheng Bailin.Impact dynamics analysis of fiber-composed structure based on centrai difference method[J].Chinese Quarterly of Mechanics, 2011, 32(3):466-472
[3]刘继先, 黄光萍.冲击响应谱试验参数的设置[J].现代雷达, 2010, 32(2):91-94 Liu Jixian, Huang Guangping.Test parameters setup of shock response spectrum[J].Modern Radar, 2010, 32(2):91-94
[4]夏晓宇.火工分离装置工作过程性能分析[D].长沙:国防科学技术大学, 2009:24-25
[5]陈敏.宇航线式火工分离装置数值模拟及优化设计[D].北京:北京工业大学, 2007:5-8
[6]白金泽.LS-DYNA3D 理论基础与实例分析[M].北京:科学出版社, 2005:150-151
[7]赵海鸥.LS-DYNA 动力分析指南[M].北京:兵器工业出版社, 2003:6-10
[8]赵铮, 陶钢, 杜长兴.爆轰产物JWL 状态方程应用研究[J].高压物理学报, 2009, 23(4):277-282 Zhao Zheng, Tao Gang, Du Changxing.Application research on JWL equation of state of detonation products[J].Chinese Journal of High Pressure Physics, 2009, 23(4):277-282
[9]李志广.钛合金螺纹连接结构预紧力、应力、可靠性分析[D].长沙:国防科学技术大学, 2007:7
[10]LSTC.LS-DYNA keyword user’s manual[G].Version 971, 2010:428
