基于多阶段决策的侦察卫星任务规划研究＊

乔熔岩，赵新国

（解放军装备学院，北京101416）

0 引言

侦察卫星是利用光电遥感器或无线电设备等侦察传感设备，从轨道上对目标实施侦察、监测或跟踪，通过搜索地面、海洋或空中来获取军事情报的人造地球卫星［1］。侦察卫星的任务规划主要涉及两个问题：一是任务分配问题，即如何把任务科学合理地分配给卫星，以最大化满足用户的需求；二是传输调度问题，即如何调配地面接收站和卫星传输信息的时间，以满足各个卫星在互不冲突的时间窗口内，传输所获得的目标信息。

目前任务规划模型主要包括：1）Gabrel［2］等人提出的基于图论的模型，将侦察卫星的任务排列转换为一个加权有向无环图，求解的目标是寻找一条最大化完成任务的路径，该模型的缺点在于无法体现完成任务所需的其他约束条件，而且模型只适用于单颗卫星；2）Vasquez［3］等人提出的背包模型，该模型的缺点是不能描述复杂任务的约束条件，而且也只适用于单颗卫星；3）Bensana［4］等人建立的更一般的线性整数规划，该模型能够描述完成任务的各个约束，但求解效率会因约束太多而降低；4）Venfaillie［5］等人提出的加权约束模型，该模型可用更自然的语言来描述约束，建立过程较为直观，但当问题较大时，求解效率较低；5）Damiani［6］等人提出的有限阶段序贯决策模型，该模型可以考虑到一些影响局部赢得的不确定因素，但对于某些复杂约束，其求解效率将成指数速度下降；6）Chien［7］等人建立的状态与活动模型，该模型可以描述超出观察活动以外的所有可能的活动，但模型没有很好的优化功能。上述的这些模型大多都适用于单星，其中的一些模型只涉及了任务分配阶段的规划，没有专门对传输调度阶段进行建模；还有一些模型将多个过程都建立在一个模型里，造成约束条件较多，目标决策过于复杂，影响了求解的效率。为解决上述问题，本文将结合侦察卫星的特点，根据任务规划不同阶段的目标决策，建立基于多阶段决策的侦察卫星任务规划模型。

1 侦察卫星的工作特点

侦察卫星具有以下特点：第一，轨道相对固定；第二，存储比较有限；第三，需要时间转换［8］（即卫星在连续执行两个以上任务时，需要有一定的时间转换，否则卫星只能完成其中一个任务）。除此之外，侦察卫星还具有数量有限、成本较高的特点，所以在规划任务时，应充分利用卫星资源，使其尽量兼顾多个任务，以弥补供需的不足。通常卫星要靠太阳能供电，其存储电池可提供应急所需的能量，所以本文在建立模型时，将假设卫星可进行全天候的工作。

2 任务分配模型

侦察卫星的任务分配是一个动态过程，但在一段时间内基本上是静态的，即各用户不会连续不断地提出任务需求。由此本文将整个规划过程，分成若干个时间段，将时间段内所提出的任务集中处理，以提高分配任务的效率。

2.1 相关定义

定义1：设集合W ＝｛w1，w2，…，wm｝表示某段时间内的侦察任务集，其中wi（ri1，ri2，…，rin）表示某项具体任务，riq表示任务wi的一个具体需求，如目标类型、侦察范围、目标分辨率等。

定义2：设集合S＝｛s1，s2，…，sk｝表示侦察卫星集，其中sj（cj1，cj2，…，cjp）表示某颗具体卫星，Cj＝｛cj1，cj2，…，cjp｝表示卫星sj的属性（性能）集，cjl（ajl）表示某一具体属性（性能），如存储量、数据传输速率、飞行轨道等，ajl表示属性（性能）cjl的具体数值或内容。

定义3：如果存在映射f，使得集合S 中的任意元素sj，都能在集合W 中找到若干个元素w1，w2，…，wk与之相对应，则称映射f 为一个任务分配策略，即。

定义3中的“对应”是指wi分配给卫星sj，但有的任务需要一颗卫星分多次侦察或多颗卫星共同来侦察，对于这种情况，可将该项任务进行分解，变成若干个由单颗卫星侦察一次就可完成的子任务，将这些子任务作为一个个独立的任务来处理，使其符合定义3。

2.2 模型的建立

根据每项任务的具体需求，结合卫星的属性（性能），建立如表1所示的对应表。

通过表1对卫星进行筛选，找出符合wi需求的拟分配卫星集Si＝｛si1，si2，…，siq｝（不考虑Si＝φ 的情况），将与完成任务wi相关的卫星属性集记为Ci＝｛ci1，ci2，…，cil｝，其中卫星sij的各属性值集合记为通 过 层 级 分 析 法［9］，可 确 定 出各卫星完成wi的质量权重集Zi＝｛zi1，zi2，…，ziq｝，将记为W 的拟分配卫星集，且SW⊆S，建立表2。

表1 对应表

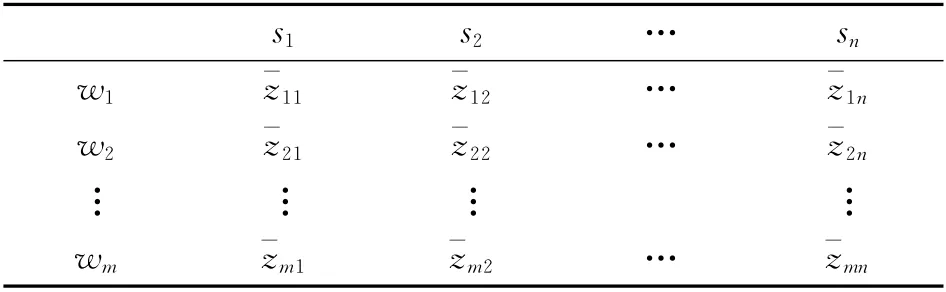
表2 完成质量权重表

在表2 中，当sj∈Si时，＝zij；当sj∉Si时，＝0。将表2转化为：

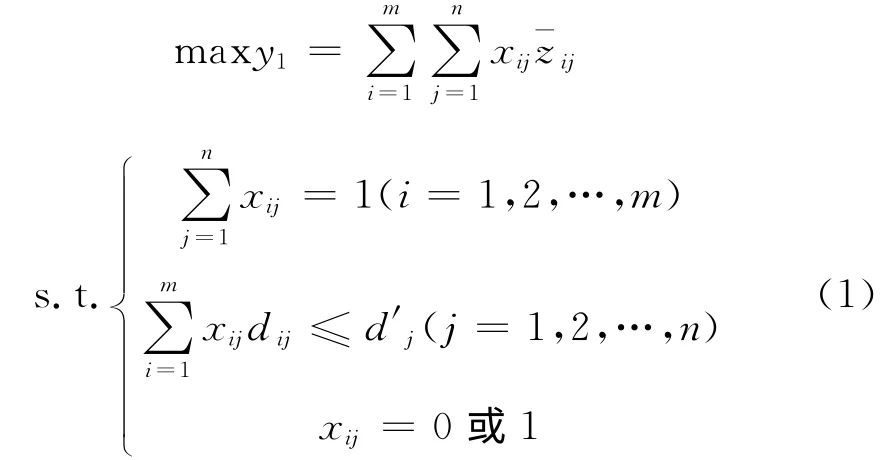
式中，xij＝1表示任务wi分配给卫星sj，否则xij＝0；dij表示完成wi需占用卫星sj的存储量，d′j表示卫星sj的剩余存储量，利用求解0-1整数规划［10］的方法，可得出卫星sj的拟分配任务集Wj。对于卫星sj来说，分配任务是一个动态过程，即在分配新任务之前，卫星sj可能还有预定的任务要完成，这就要求新任务不能与原有任务发生冲突，而且新任务之间也不能有冲突，为此本文建立如图1所示的任务关系图。

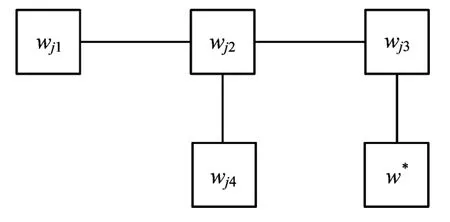
图1 任务关系图

图1中集合Wj＝｛wj1，wj2，wj3，wj4｝，w＊为原有待完成的任务，将有冲突的两个任务用直线连接，为找出合理的分配方案，进行如下的图上作业法：1）将原任务和与原任务有连线的新任务在图中删除（包括连线），即删除w＊和wj3；2）在剩下的图中，找出连线最多的任务，即任务wj2；3）找出将与任务wj2没有冲突的任务，并将它们和wj2编成一组，记为分配策略1；4）将策略1中的任务（包括连线）在图中去除；5）在剩下的图中重复第二步骤操作，以此类推，直到把任务全部编组完成；6）比较各分配策略，找出包含任务最多的编组，将该编组作为sj的分配策略Wj0（即初始分配策略）。

按照上述的方法，可以求出每颗卫星初始任务的分配策略，然后求出，其 中W′＝｛w′1，w′2，…，w′k｝表示没有分配到卫星的剩余任务集，建立式（2）：

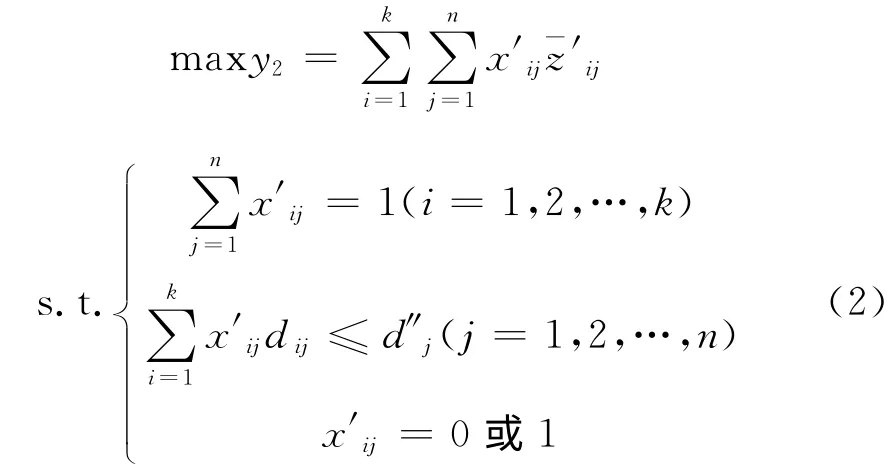
式中，当w′i∈Wj时（避免重复冲突），当w′i∉Wj时，d″j表示卫星sj在假设完成Wj0中任务后，还剩余的存储量。通过对式（2）的求解，又可建立各卫星新的任务关系图，然后按照图上作业法，确定出新的分配策略，以此类推，直到把所有任务都分配完毕或各卫星均已达到饱和状态为止。将最终的分配策略记为定义3中的映射f，如果此时还有任务没有被分配，则这些任务只能等待各卫星完成任务后，重新参加下一轮的分配。

2.3 模型的改进

上述的分配模型主要以卫星完成任务的质量为参考标准，该模型适用于常规任务的分配需求，而在实际中，有时会出现一些紧急任务或需求用户的级别较高，用户需要卫星及时提供某区域的情报，这就要求分配任务时，不但要考虑卫星的性能，还要考虑执行侦察的时段和完成任务的时限，为解决这一问题，本文将建立如下的改进模型：

根据任务wi的级别将W 分为两类，即优先任务集W（1）和普通任务集W（2），其中W（1）包括紧急任务和高级别用户的任务，W（2）包括非紧急的常规任务，且满足W ＝W（1）∪W（2），W（1）∩W（2）＝φ。在分配卫星资源时，应首先保障W（1）中的任务，然后再考虑W（2）中的任务。假设通过表1确定出为完成W（1）的拟分配卫星集，集合表示各卫星完成侦察的最短延迟时间，其中表示卫星完成任务的最小时延，其大小等于飞到侦察区域的时间加上执行侦察的时间。定义卫星完成任务的效能权重为，其中为卫星完成任务的质量权重，e为调节系数。下面建立目标决策模型，如式（3）所示，其中表示任务占用卫星的存储量表示卫星的剩余存储量，但与式（2）中的d′j不同，因为现在所要执行的是优先级任务，如果原来预定的任务不是优先的，其数据可以被替代，以确保优先级任务的完成，所以的值只是存储总量与预定优先级任务所需存储量的差。

3 传输调度模型

将地面接收站集记为集合G＝｛g1，g2，…，gk｝，假设一个接收站在同一时间内，只能接受一个卫星的数据，通常情况下，集合S 与G 不是一一对应关系。一般接收站都会先满足优先级任务，而当多个卫星都承担优先级任务时，就要尽量避免这些卫星在有冲突的时间段进行数据传输，为解决这一问题，本文将建立如下的传输调度模型：

第一步，将矩阵中每一列的数值相加，找出实数部分最小的一列，并选出该列所对应的时间窗口，例如或（这里以为例）；

第七步，检验剩下的矩阵，如果该矩阵为零矩阵，则停止操作，将该矩阵中的时间窗口记为一个调度策略

第八步，将策略1中的时间窗口在式（4）中删除，然后重复第一步的操作，以此类推，直到找出新的策略为止，例如策略

第九步，比较各个策略，找出包含时间窗口数最多的一个，如果数量相同，则选择完成时延最小的一个策略。例如策略和假设对于用户来说，卫星选择比选择的时延要小，而对于和来说，选择和要比选择和的时延要小，那么综合比较就采用策略

4 结束语

本文结合侦察卫星的工作特点，依据任务规划不同阶段的目标决策，建立了基于多阶段决策的侦察卫星任务规划模型，即任务分配模型和传输调度模型。该模型首先将任务进行分级和分解，然后根据对应表建立拟分配任务的卫星集，从而缩小所涉及卫星的范围，以减少目标决策的数量规模，利用层次分析法确定卫星完成任务的效能权重，并建立任务分配的决策模型；为避免计算的复杂性，分配模型中的约束没有涉及完成任务时可能出现的时间冲突，而是在得出拟分配方案后，利用所建立的任务关系图，通过图上作业法来解决，以此使得分配模型更加简明，计算流程更加清晰，从而提高求解的效率；为解决卫星传输数据时可能发生的冲突，本文根据假设的情况，建立了卫星传输时间的关系矩阵，给出了一种求解模型的基本方法，从而较好地解决了这一问题。综上所述，本文建立的基于多阶段决策的侦察卫星任务规划模型，具有一定的理论与应用价值。■

［1］王永刚，刘玉文.军事卫星及应用概论［M］.北京：国防工业出版社，2003.

［2］Gabrel V，Vanderpooten D.Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite［J］.European Journal of Operational Research，2002，139（3）：533-542.

［3］Vasquez M，Hao JK.A “Logic-constrained”knapsack formulation and a Tabu algorithm for the daily photograph scheduling of an earth observation satellite［J］.Computational Optimization and Applications，2001，20（2）：137-157.

［4］Bensana E，Verfaillie G，Agnese JC，et al.Exact and approximate methods for the daily management of an earth observing satellite［C］∥Munich，Germany：Symposium on Space Mission Operations and Ground Data Systems，1996.

［5］Bensana E，Verfaillie G.Exact and approximate methods for the daily management of an earth observation satellite［C］∥Proceeding of the 4th International symposium On Space Mission Operation and Control Date System，1996.

［6］Verfaillie G.Russian doll search for solving constraint optimization problems［C］∥Portland，Oregon，USA：Proceedings of AAAI-96，1996.

［7］Chien S，Sherwood R，Rabideau G.The Techsat-21 autonomous space science agent［C］∥Proc of the 1st International Conference on Autonomous Agents.NewYork：ACM Press，2002.

［8］黄文清，等.空间信息系统建模与效能仿真［M］.北京：解放军出版社，2010：96-97.

［9］胡运权.运筹学教程［M］.北京：清华大学出版社，2007.

［10］陈庆华，等.装备运筹学教程［M］.北京：国防工业出版社，2007.

［11］陈庆华，吕彬，李晓松.系统工程理论与实践［M］.北京：国防工业出版社，2011.

［12］陈宝林.最优化理论与算法［M］.2版.北京：清华大学出版社，2005：37-50.