基于ANSYS的输电线路钢管杆结构稳定性分析

王彦海，谢守辉

（1. 三峡大学 电气与新能源学院，湖北 宜昌 443002；2. 中国南方电网超高压输电公司 广州局，

广东 广州 510420）

在架空输电线路领域，由于钢管杆具有占用线路走廊窄、结构简单、造型美观、工厂化生产和维护工作量小等优点，近年来，在城市和市郊应用越来越广泛[1-4]。钢管杆固定形式为底端固定、顶端自由，长细比较大，在外荷载作用下易发生失稳破坏，因此需要对钢管杆进行结构稳定性分析。在稳定性分析中，用常规方法计算失稳临界荷载非常困难，但采用成熟的有限单元法能够方便地解决这个问题。本文利用有限元分析软件ANSYS，建立了钢管杆的三维有限元模型，进行了5种工况下特征值屈曲分析[4-9]。

1 稳定性分析原理

屈曲又称作失稳，用于表示结构和构件保持原有形状的能力。特征值屈曲分析属于线性分析，用于预测理想线弹性结构的理论屈曲强度，计算速度较快。特征值屈曲是以小位移小应变的线弹性理论为基础的，分析中不考虑结构在受载变形过程中结构形状的变化，也就是在外力施加的各个阶段，总是在结构初始变形上建立平衡方程[10-11]。

假设结构的应力刚度矩阵为［Kσ］，荷载乘子为λ，则λ·［Kσ］是对应某一强度的应力刚度矩阵。线性条件下，［Kσ］和线性刚度矩阵［K］均不是位移函数，而在作用荷载［R］保持不变时，如果位移矩阵为［U］，虚位移矩阵为［U軓］，为了使状态［U］和［U+U軓］保持平衡状态，必须满足方程1和方程2。

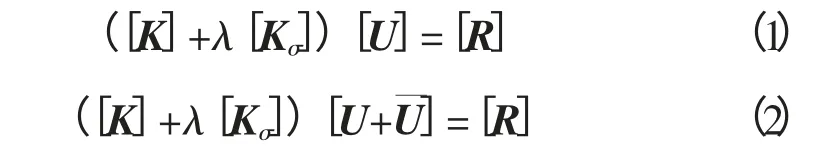
方程2减去方程1得：

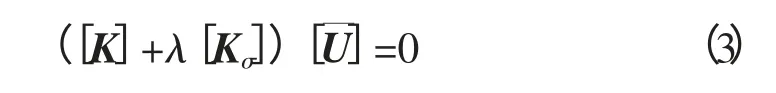
由方程（3）可求解出特征值λ和特征矢量［U軓］，当施加的初始荷载为单位荷载时，λ即是失稳临界荷载，如果求得的λ是负值，则表示要在相反方向施加荷载结构才会发生屈曲，特征矢量［U軓］表示屈曲形状。在屈曲分析中，通常只需求解结构的第一特征值和特征矢量。

2 钢管杆有限元建模

利用有限元分析软件ANSYS对钢管杆的稳定性进行分析计算。

2.1 工程概况

该钢管杆用于110 kV架空输电线路，双回路架设，钢管杆截面形式为正八边形，梢径400 mm，根径800 mm。钢管杆分三段套接连接，下面两段厚度为8 mm，上面一段厚度为6 mm。导线选用LGJ-240/40，地线选用GJ-50，水平档距为200 m，垂直档距为210 m。钢管杆的结构尺寸如图1所示。

图1 钢管杆结构尺寸Fig. 1 Structures and sizes of the steel pole

2.2 建立模型

钢管杆稳定性分析建模内容主要包括：定义单元类型、定义材料特性、建立几何模型和划分网格等。

1）定义单元类型。钢管杆属于空间实体，根据现行设计标准和钢管杆的受力特性，定义单元类型时选用Solid45三维实体单元，其单元体具有8个节点，每个节点有3个自由度，适合模拟各向同性的实体结构。

2）定义材料特性。根据特征值屈曲分析原理，钢管杆材料特性定义为各向同性线弹性，其中弹性模量为206 GPa，泊松比为0.28，不考虑温度的影响。

3）建立几何模型。该钢管杆为不等径拔梢形，截面形式为正八边形，采用自下向上创建有限元模型方法比较方便，即先计算出钢管杆底面、顶面、横担等处各关键点的坐标，然后在ANSYS中输入关键点坐标，再由关键点生成体。由于正八边形钢管杆为对称结构，建模时可利用镜像功能快捷建模。建立的钢管杆实体模型如图2所示。

图2 钢管杆实体模型图Fig. 2 The physical model figure of the steel pole

4）划分网格。实体建模的最终目的是为了划分网格，以生成节点和单元，网格数量的多少将会影响计算结果的精度和计算规模的大小。一般来讲，网格数量增加，计算精度会有所提高，但计算规模也会增加；相反计算精度和计算规模则会降低。在结构分析时计算精度和运算时间应权衡考虑，不可为了提高不必要的精度而盲目增加网格数量。根据钢管杆稳定性分析目的和选用的单元类型，通过智能网格划分控制设置网格划分精度为默认状态。钢管杆网格模型如图3所示。

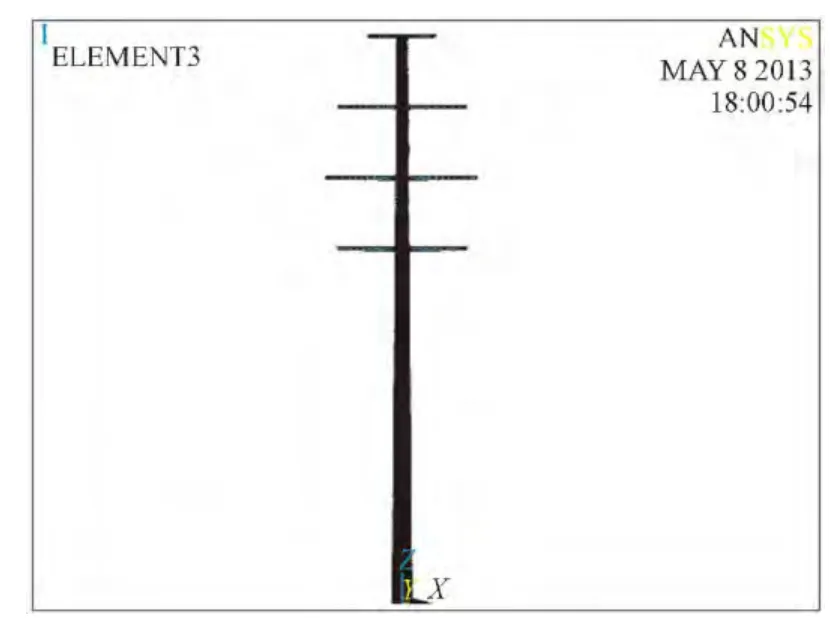
图3 钢管杆网格模型图Fig. 3 The mesh model of the steel pole

3 钢管杆稳定性分析

3.1 施加约束和荷载

根据钢管杆加工制造和施工工艺，认为钢管杆底部以及主杆和横担连接处能够承受弯矩和扭矩，即施加约束线性位移Ux=0、Uy=0、Uz=0，角度位移ROTx=0、ROTy=0、ROTz=0。

作用在钢管杆上的荷载主要有导地线自重、覆冰荷载、风荷载和导线张力等。根据荷载组合原则，分析5种工况下钢管杆的稳定性，它们分别是正常运行工况Ⅰ、正常运行工况Ⅱ、断导线工况、断地线工况和安装工况。

3.2 计算结果

对钢管杆荷载组合5种工况加载并求解，考虑钢管杆自重，计算时通过改变施加荷载F值的大小，重复求解过程，当计算出的特征值等于或接近1时，施加的荷载F即为失效临界荷载，并提取第一阶特征值，查看相应屈曲模态形状。各工况下的计算结果见表1，屈曲模态形状见图4—图8。

表1 稳定性计算结果Tab. 1 Stability calculation results

图4 正常运行工况ⅠFig. 4 Normal operating condition Ⅰ

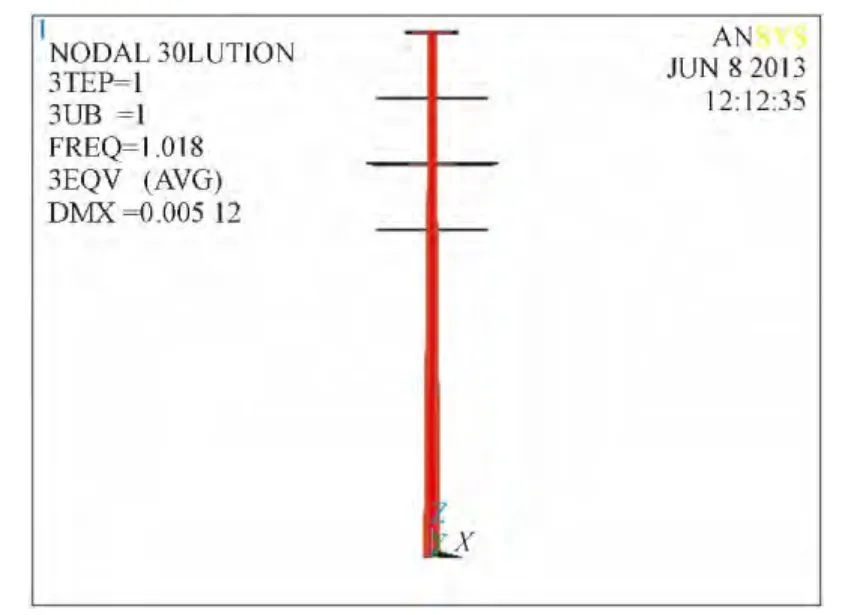
图5 正常运行工况ⅡFig. 5 Normal operating condition Ⅱ

图6 断导线工况Fig. 6 Conductor -broken conditions

图7 断地线工况Fig. 7 Grounding-wire broken conditions

图8 安装工况Fig. 8 Installation conditions

4 结论

1）从5种工况的计算结果来看，误差均在允许范围内，断导线工况屈曲荷载值比其他4种工况要小，因此架空输电线路断导线时，结构最容易失稳。

2）用常规方法分析钢管杆稳定性非常困难，借助有限单元法比较容易解决这个问题，为ANSYS分析钢管杆稳定性提供借鉴。

[1] 王麦锋，吴亮，鞠浩. 750 kV输电线路铁塔选型和规划[J]. 电网与清洁能源，2012，28（11）：45-51.WANG Maifeng，WU Liang，JU Hao. Selection and planning of steel towers for the 750 kV transmission line[J].Power System and Clean Energy，2012，28（11）：45-51（in Chinese）.

[2] 薄学微，王黎明，孙保强. 500 kV紧凑型线路复合相间间隔棒机电性能研究[J].高压电器，2011，47（2）：43-47.BO Xuewei，WANG Liming，SUN Baoqiang，et al. Study on electrical and mechanical properties of phase-to-phase composite spacer on 500 kV compact line[J]. High Voltage Apparatus，2011，47（2）：43-47（in Chinese）.

[3] 黄誉，邓洪洲，金晓华. 钢管杆塔新型内外法兰受弯性能试验研究及有限元分析[J]. 建筑结构学报，2011，32（10）：73-81.HUANG Yu，DENG Hongzhou，JIN Xiaohua. Experimental research and finite element analysis on flexural performance of innovative flange joint used in steel poles[J]. Journal of Building Structures，2011，32（10）：73-81（in Chinese）.

[4] 涂崇巍，郭耀杰. 钢管杆输电线路中K值的取值原则[J].武汉大学学报：工学版，2008，41（7）：247-251.TU Chongwei，GUO Yaojie.Criteria of choosing K value for transmission line of steel pipe poles[J]. Engineering Journal of Wuhan University，2008，41（7）：247-251（in Chinese）.

[5] 高军. 圆柱头盘形悬式瓷绝缘子的结构优化设计[J]. 电瓷避雷器，2013（2）：24-27.GAO Jun. Structural optimization of cylindrical disk suspension insulator[J].Insulator and Surge Arrester，2013（2）：24-27（in Chinese）.

[6] 朱洪祥，马明，宋涛，等. 天津慈海桥摩天轮结构的稳定性分析[J]. 建筑结构，2007，37（3）：69-71.ZHU Hongxiang，MA Ming，SONG Tao，et al. Stability analysis of skyscraper wheel structure in Tianjin Cihai Bridge[J]. Building Structure，2007，37（3）：69-71（in Chinese）.

[7] 吴海洋，余焘，谭青海，等. 输电铁塔刚架模型和桁梁混合模型静态强度及稳定分析[J]. 华北电力技术，2011（5）：6-10.WU Haiyang，YU Tao，TAN Qinghai，et al. Analysis of static strength and stability for rigid frame model and hybrid model about transmission tower[J]. North China Electric Power，2011（5）：6-10（in Chinese）.

[8] 姜顺先，王存堂，于浩源. 格构式钢管混凝土风力发电塔架设计[J]. 辽宁工程技术大学学报: 自然科学版，2012，31（2）：202-205.JIANG Shunxian，WANG Cuntang，YU Haoyuan.Design of wind turbine tower using lattice concrete-filled steel tube[J].Journal of Liaoning Technical University: Natural Science，2012，31（2）：202-205（in Chinese）.

[9] 郑夕健，谢正义，张国忠. 基于ANSYS的塔式起重机结构稳定性分析[J]. 建筑机械，2007（11）：76-81.ZHENG Xijian，XIE Zhengyi，ZHANG Guozhong. The stability analysis of the tower crane based on ANSYS[J].Construction Machinery，2007（11）：76-81（in Chinese）.

[10] 李国栋，石祥彬，刘学，等. 直接空冷机组大直径排汽管道的结构稳定性分析[J]. 热力发电，2007（4）：38-43.LI Guodong，SHI Xiangbin，LIU Xue，et al. Analysis of structural stability for large diameter exhaust steam piping of direct air-cooling unit[J]. Thermal Power Generation，2007（4）：38-43（in Chinese）.

[11] 王泽军. 锅炉结构有限元分析[M]. 北京：化学工业出版社，2005.