电力系统无功优化研究综述

党存禄，张宁，邵冲

（1. 兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050；2. 甘肃省电力公司电力科学研究院，甘肃 兰州 730050）

随着我国电力工业的迅速发展和电力系统规模的不断扩大，电网结构日趋复杂，用户对电网电能质量也提出了更高的要求。无功优化作为电网经济安全运行的重要组成部分，日益受到人们的重视与关注。电力系统无功优化是指在电力系统无功电源较为充裕的情况下，通过调节发电机机端电压、调整变压器抽头变比、改变无功补偿装置的出力等措施来调整无功潮流，使得系统电压值达到合格值，同时全网有功损耗最小。

电力系统的无功优化问题是一个多变量、多约束的混合非线性规划问题，其操作变量既有连续变量（如节点电压、发电机的无功出力），又有离散变量（如变压器分接头位置、补偿电抗器和电容器的投切容量），使得优化过程十分复杂。长期以来，国内外的许多专家、学者对此进行了大量的研究和探索，取得了很多成果。传统的数学方法有：线性规划法[1]、非线性规划方法[2]、简化梯度法[3]、序列二次规划法[4]、牛顿法[5]、内点法[6]等，这些方法各自都有一定的适应性和优越性，但不能很好地处理离散变量。随着计算机技术的发展和人们对于人工智能算法的不断探索，越来越多的智能优化算法应用于无功电压优化中，如遗传算法[7]、模拟退火算法[8]、粒子群算法[9]、免疫算法[10]、搜索禁忌[11]算法等。这些优化算法各有各的优点和适应性，随着人们对于优化结果要求的提高，单一使用一种优化算法得到的结果已经不能满足人们的要求。所以本文在总结了现有智能优化算法改进的基础上，把研究重点放在了智能优化算法的混合策略上，并且对于动态无功优化也进行了一定地研究和介绍。

1 无功优化的数学模型

1.1 目标函数

以往人们对于无功优化的数学模型只考虑网损最小，没有考虑其他方面的情况。本文在建立无功优化模型的时候，在考虑系统网损最小的基础上，还加入了静态电压稳定裕度、调控费用这两个指标。既然是多目标优化问题，那么如何确定权值就成为了一个核心问题。文献[12]提出将多个目标函数进行归一化处理再加权值，其中权值可以根据具体情况而定。

1）系统网损。系统网损为:

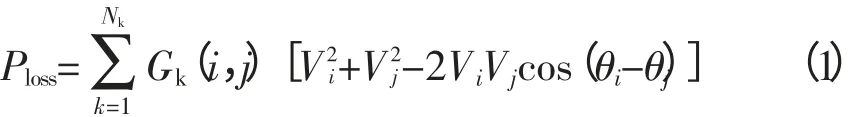
式（1）中，Nk为系统支路数；Gk（i，j）为支路的电导；Vi、Vj、θi、θj为节点的电压幅值、相角。

2）静态电压稳定裕度δ。δ为对角元［δ1，δ2，…，δ2（n-1）］中的最小值。当电力系统运行方式由正常工作点向稳定极限过渡时，雅可比矩阵J向奇异的方向变化，当系统电压达到静态稳定极限时，J奇异。由于δ反映了J接近奇异的程度，因此可用δ作为电力系统的静态电压稳定裕度指标。

3）调控费用。调控费用为：

式（2）中，m为可调设备数量；Ti为第i台设备动作次数；φi为第i台设备动作一次的费用，φi由设备造价和设备使用寿命求得。

1.2 约束条件

不等式约束条件为:

式中，T为变压器变比；C为并联电容器投切容量；Q为发电机无功出力大小；V为节点电压。

等式约束条件即潮流方程为:

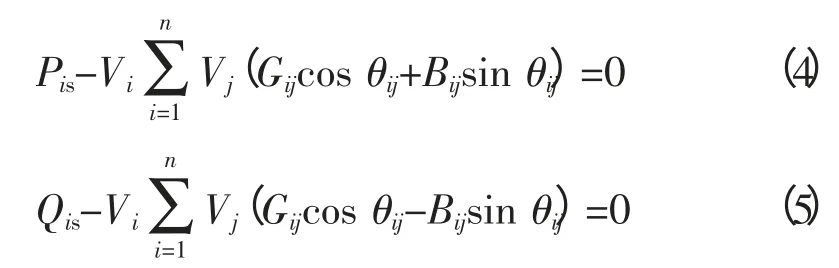
1.3 归一化处理及权系数选取

由于各个目标之间数量级不统一，故先对3个指标进行归一化处理。

把3个目标进行加权得目标函数为:

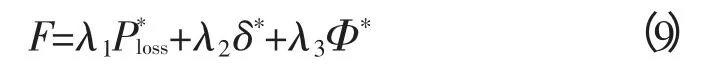
式（9）中，λ1、λ2、λ3为各个目标的权重，须满足λ1+λ2+λ3=1，式中λ1≥0，λ2≥0，λ3≥0。

本文按照排序法进行权值选取，为方便叙述设有P个目标需要确定权重，步骤如下：

1）先求P个单目标问题:min fi（x）（i=1，2，…，P）的最优解为xi（i=1，2，…，P）。

4）计算均差:

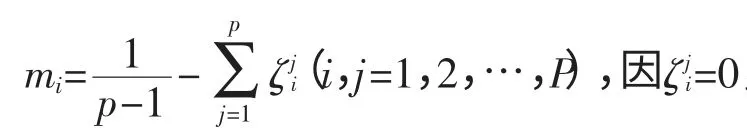
6）将mi从大到小排序，设mi1≥mi2≥…≥mip，则对应有λi1≥λi2≥…≥λip≥0，且满足

7）构造目标函数，按照排序结果将均差大的目标函数乘以小的权系数，而均差小的目标函数乘以大的权系数，即:

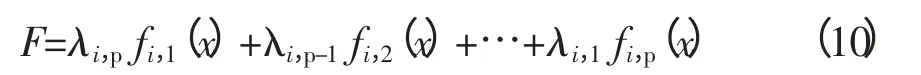
从数学的角度来说，这样求出来的有效解基本上是比较满意的，在实际中也可结合电力系统的特性，根据经验做出适当调整。

2 智能优化算法在无功优化中的应用

虽然智能优化算法相对于传统的无功优化算法已经取得了很大进步，但是随着电力系统的规模不断扩大，电网结构日益复杂，以及人们对于电能质量要求的提高，这就要求研究者要对现有的智能优化算法不断地进行改进，并且提出各种算法的混合策略。

2.1 改进的智能优化算法在无功优化中的应用

2.1.1 改进的遗传算法

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。文献[13]针对无功优化中连续变量和离散变量共存的特点，对简单遗传算法编码方式、交叉算子和变异算子进行了重新确定。为了使算法能较快收敛并且能以较大的概率跳出局部最优，提出了一种改进自适应变异概率遗传算法。改进的自适应变异概率既考虑了种群中个体的适应度值情况，同时也计及了算法所处的阶段。该方法既能保持典型自适应概率较快收敛的特性，又通过在算法后期产生的更多新基因维持种群多样性，从而拥有更强的寻优能力，通过算例验证了所求得的有功网损更小。文献[14]针对传统遗传算法中存在的易陷入局部最优解和后期收敛速度慢的问题，在简单遗传算法（SGA）的基础上，提出更加有效的算法，即改进遗传算法（IGA）。新算法结合灵敏度分析产生原始个体替代SGA，SGA的交叉和变异被改进，改进的交叉操作拥有快速局部调节能力，改进的变异操作引入灵敏度分析产生新的个体。在负载分区的基础上运用灵敏度来决定补偿母线，目的是为了分散补偿和减少遗传算法的搜索空间。最后通过算例分析验证了改进交叉和变异的操作提高了遗传算法的性能。文献[15]提出一种改进小生境遗传算法来克服小生境遗传算法中小生境难以确定的不足，改善遗传算法容易陷入局部收敛和早熟的缺点。通过模糊动态聚类分析方法实现小生境群体的划分，然后利用适应度共享技术对小生境内个体适应度进行调整，以提高全局寻优能力。提出和运用隔代小生境共享机制、最优个体邻域搜索及保留策略等以提高算法的计算速度和收敛速度。

2.1.2 改进的粒子群算法

粒子群算法由于自身特点和优势，特别适用于解决像电力系统这样的多目标、多约束的混合优化问题。文献[16]在传统的电力系统无功优化问题的基础上，建立了同时兼顾电力系统有功网损最小和电压偏移最小的多目标无功优化模型，并且针对多目标优化问题，提出了一种改进的多目标粒子群算法。该算法利用计算非支配排序和拥挤距离方式更新粒子的个体最优值和全局最优值，并保留每一次迭代后的一部分精英解集，最终结果在精英集合中找寻所需的Pareto前端；引入变异算子和动态权重算子，增强了寻优能力，降低了结果早熟和陷入局部最小值的可能。最后将该算法应用于IEEE 14节点系统进行测试，结果表明该算法不仅实现了系统经济运行，同时也提高了电网的电压稳定，并且为用户提供了多样化的解集，方便用户根据实际情况灵活选择。文献[17] 针对传统粒子群优化算法“早熟”与后期收敛速度慢的缺点，提出了一种基于并行自适应粒子群优化算法的电力系统无功优化方法。该方法首先将初始种群随机划分成N个子群，然后分别在各子群中以所提方法寻优，从而实现了算法的并行计算。为避免各子群陷入局部最优解，采用二值交叉算子使各子群间的信息共享并更新相关粒子位置，保证了算法的全局搜索能力，并维持了种群的多样性。同时，各子群寻优过程中，根据利己、利他及自主3个方向对当前搜索方向自适应更新，提高了算法的收敛速度。

2.2 混合优化算法在无功优化中的应用

2.2.1 以遗传算法为基础的混合优化算法

非线性内点法具有收敛性好、寻优速度快、鲁棒性强的突出优点，适宜求解连续可微的函数优化问题，但难以处理离散变量；遗传算法通过对优化变量的随机组合来获取全局最优解，适宜求解各种离散优化问题，但遗传算法寻优速度慢，在一定条件下容易陷入局部最优值。文献[12]将遗传算法和内点法相结合求解电力系统无功优化问题。改进了传统的遗传算法，采用混合编码和动态调整选择、交叉、变异算子，并在适应度函数中引入了内点法的对数障碍函数，有效地解决了实际系统的离散变量和状态变量易在边界取得的问题。

群搜索优化（GSO）算法[18-19]近年来也开始被应用到电力系统优化问题，其具有处理大规模多变量优化问题不敏感的优点。为适应处理无功优化问题，文献[20]提出了基于邻域搜索的GSO算法，即NGSO算法。该算法容易实现且具有较强局部搜索能力，不容易陷入局部最优，但由于其在邻域范围内逐步搜索，因此全局搜索能力较差。由于遗传算法和NGSO算法在原理上具有互补特征，所以研究者提出了一种综合两种算法优势的新型无功优化混合算法来求解无功优化问题。该混合算法采用两种算法交替求解，既发挥了遗传算法的全局收敛性能，又利用了NGSO的局部搜索能力，有效地保证了混合算法的整体寻优效率。

2.2.2 以粒子群算法为基础的混合优化算法

粒子群算法采用并行搜索方式，其收敛速度较快，易于实现，需要调整的参数少，适合工程应用，但容易陷入局部最优。针对这一特性，文献[21]提出了基于改进粒子群算法和预测-校正内点法的解耦无功优化算法。通过引入时代因子和邻近变异策略，同时采用分段处理方法对粒子群算法进行改进。运用预测-校正算法替代原-对偶内点，使得在内点法寻优过程中的迭代步长加大，同时避免寻优过程中振荡的出现。将改进粒子群算法和预测-校正内点算法分别用于无功优化的离散优化和连续优化子问题，这样使整体的寻优速度更快，效果更佳。

文献[22]考虑多目标的无功优化问题，提出了一种新的优化算法，为BPSO和变邻域差分进化算法的混合算法。粒子群算法是一种基于社会群体行为的全局优化算法，它具有并行处理的特点，而BPSO在经过多次迭代后，粒子多样性逐渐降低容易陷入局部最优，因此采取将变邻域搜索算法与BPSO相结合，变邻域搜索算法具有很好的全局性能够改善BPSO“早熟”的缺陷，从而求出无功优化的最优解。

文献[23]针对粒子群无功优化中由于随机生成代表控制变量值的粒子，使得在优化迭代过程中易陷入局部最优解，而且后期收敛速度慢等问题，将混沌优化算法融合到粒子群算法中，提出了混沌粒子群算法求解多目标无功优化问题。该算法在初始化粒子即无功优化控制变量值时，采用混沌思想，增加控制变量取值的多样性；通过粒子群无功优化算法计算各个粒子对应的适应值即无功优化目标函数值，并按照其大小择优选取控制变量值进行混沌优化以帮助无功优化控制变量跳出局部极值区域；并根据无功优化目标函数值自适应地调整其惯性权重系数以提高全局与局部搜索能力。通过算例分析表明，采用自适应混沌粒子群算法进行无功优化，能够及时跳出局部最优得到全局最优解，且收敛速度快。

文献[24]提出了一种针对粒子群算法局部搜索能力较弱和存在早熟收敛的问题，将禁忌搜索思想融入到粒子群算法中的混合算法。该方法在粒子群算法寻优过程的后期加入了禁忌表，扩大搜索空间，避免陷入局部最优。这两种方法优势互补，很好地解决了PSO搜索后期难以收敛的问题。

2.3 新型优化算法在无功优化中的应用

除了以上介绍的一些改进的智能优化算法和混合的优化算法外，研究者也不断地探索出新的优化算法来适应现代电力系统无功优化的需要。以下介绍几类新型优化算法，它们不论是从数学模型还是优化算法方面都有了一定的创新，为无功优化的研究开辟了新的方向。

为了在在线无功电压控制中协调考虑系统的安全性和经济性，文献[25]提出了一种基于多目标优化的无功电压优化模型。除传统的经济目标外，该模型将系统的静态安全性加入到寻优目标中，以同时寻求系统经济性和安全性的最优化。基于合作博弈理论，提出了该模型的求解方法。在博弈过程中，经济目标和安全目标作为博弈参与方轮流给出决策策略，直至博弈达到均衡。

基于帕累托最优概念的多目标进化算法在电力系统无功优化领域已有广泛应用，但目前通过某种单一算法求解的方式由于进化算子的唯一性，难以保证进化过程不同寻优阶段的普适性和鲁棒性，因此文献[26]提出一种基于多种进化算法自适应选择的多目标无功优化方法。通过分析已有多目标进化算法的特征，考虑协调性与互补性，建立包含4类算法的备选池；在进化过程不同阶段根据寻优性能自适应地确定备选算法的使用比例，从而综合多种算法的性能优势，提高整体寻优效率。

文献[27]中建立了无惩罚因子策略的数学模型，并应用改进细菌群体优化（BCC）算法进行无功优化。该模型利用可行细菌的占比指导细菌向可行空间搜索或最小网损空间搜索，快速搜索到可行的最优值。在基本BCC算法中引入速度、感知范围的动态调整以及高斯变异机制以提高寻优精度；同时引入映射因子以改善BCC算法解决离散域问题的性能。算例结果表明，改进BCC算法具有较好寻优性能，结合无惩罚因子策略的数学模型能快速得出合理的无功优化策略。

文献[28]针对无功优化分解协调模型求解中增广拉格朗日函数不可分的问题，在邻近中心算法基础上提出一种适用于特殊等式约束优化问题、可实现所有步骤分解计算的全分邻近中心算法。该算法通过邻近函数构造平滑同时可分的拉格朗日函数，并通过最优梯度更新拉格朗日乘子，只需要在相邻分区之间交换边界节点信息即可实现全网无功优化的分解协调计算。与通过对偶梯度更新拉格朗日乘子的分解算法相比，它不但可以直接确定计算所用参数，而且可以大大提高收敛速度。算例结果表明，所提算法可以实现全网无功优化的分解协调计算，并且其计算效率远高于基于辅助问题原理的分解协调算法。

3 动态无功优化算法

随着无功优化研究地深入，许多学者又提出了动态无功优化的概念。动态无功优化[29]是指在网络结构参数及未来一天各种负荷母线的有功、无功变化曲线及有功电源处理给定的情况下，通过调节发电机的无功出力、电容器组的出力及有载调压变压器的分接头，在满足各种运行约束的条件下，使整个电网的电能损耗最小。由于其动作是不连续的，且一天动作的总次数又有限制，所以当考虑到负荷一天的变化时，这种限制必然导致各时段的无功调度和电压控制存在强耦合。因此动态无功优化问题实际上是一个十分复杂的时空分布、非线性混合整数动态优化问题。对于这样一个问题，要找出全局最优解十分困难。通常做法是在计算效率和全局最优二者中取折中，即在简化模型的基础上求得一个较好的优化结果。

动态无功优化与静态无功优化在概念上有差异，导致了它们的数学模型也有很大的区别。动态无功优化算法主要有以下4种：动态规划法、非线性混合整数优化法、人工智能方法和其他数学计算方法。其中人工智能优化算法现在被广泛地应用于动态无功优化问题，并且取得了令人满意的结果。

文献[30]针对存在离散控制设备动作次数约束的动态无功优化问题，提出免疫遗传算法和非线性内点法的混合算法。首先忽略控制设备的离散性和动作次数约束，采用非线性内点法求解初始优化解；然后按照控制变量的性质将原问题分解为连续优化与离散优化2个子问题迭代求解。在离散优化问题中，保持连续变量不变，采用免疫遗传算法优化离散变量，通过特别的编码方式使抗体自动满足动作次数约束；在连续优化问题中，保持离散变量不变，采用非线性内点法优化连续变量。混合算法充分结合了免疫遗传算法和非线性内点法的优点，能较快求解动态无功优化的近似最优解。

文献[31-32]提出为满足并联电容器开关或有载调压变压器分接头等离散控制设备最大允许动作次数的限制，根据负荷变化情况提出采用全天各时段的离散控制设备延缓动作时间来避免不必要的调节。运用层次聚类法和引入种群多样性思想，提出一种求解动态无功优化的改进蚁群算法。该算法用各时段的离散控制设备动作次数修改初始信息素；在每个时段优化过程中，对系统各节点灵敏度进行聚类分析后确定信息素变化量，并用离散控制设备的动作次数对其修改。

文献[33]提出为解决应用内嵌离散惩罚的非线性原对偶内点法求解离散整数动态无功优化模型时产生的“维数灾”问题，对修正方程用块矩阵解耦的算法做进一步探讨，提出了两次求解修正方程系数矩阵并三角分解，从而降低动态无功优化应用于大电网时的数据存储量的新思路，即以时间换取空间（定义为时空转换）。最后在两个实际系统上的优化计算表明，所提算法既能计算大电网的动态无功优化，又具有较快的计算速度。

4 总结与展望

电力系统无功优化问题是电力系统优化问题研究的重要内容之一。首先，本文介绍了现阶段无功优化数学模型的建立中，当考虑多目标函数时用加权归一化方法确定权值的情况，同时还介绍了基于新理论的考虑多个性能指标的一些建模方法，这使得现代电力系统无功优化问题得到的结果更加合理准确，更能满足人们需求。其次，本文在总结无功优化算法的基础上，重点介绍了几种改进的智能优化算法，它们在原有的算法上有了很明显的创新，并且不管是在计算速度上还是计算精度上都有了很大的提高。对于混合的智能优化算法，各种混合策略使得智能优化算法分别发挥自己的优势，弥补了各自的缺点，从而提高了算法的寻优效率。最后，本文还简单介绍了动态无功优化问题的优化算法，其中主要是智能优化算法的应用，虽然单一的智能优化算法存在“早熟”或者全局收敛性不够好的问题，但是它善于处理离散变量，只要对其进行改进或采用优化算法的混合策略就能很好地解决这些问题，并且得到人们满意的结果。

现阶段人们对于传统无功优化问题的研究已经比较成熟，不管是从数学模型的建立还是优化算法上都取得了一定的成果。那么接下来就需要对于动态无功优化问题进行进一步地探索和研究。由于动态无功优化概念的提出相对比较晚，相关的研究也比较少，但是动态无功优化问题和静态无功优化问题有着同样重要的意义。与此同时，还应该对于新的电力系统环境下的无功优化问题进行一些思考，比如含有分布式发电的配电网无功优化的研究和含有风电机组配电网无功优化问题的研究等。相信随着各种研究工作的深入以及优化算法的发展，无功优化方法会日益完善，在电力系统中充分发挥其重要的作用。

[1] DELSON J K，SHAHIDEHPOUR S M.Linear programming applications to power system economics[J]. Planning and Operations，IEEE Transactions on Power Systems，1992，7（3）：1155-1163.

[2] LAI L L，MA J T. Application of evolutionary programming to reactive power planning-comparison with nonlinear programming approach[J]. IEEE Transactions on Power Systems，1997，12（1）：198-206.

[3] 丁明，张晋波，汪兴强. 提高预处理共轭梯度法计算大型电网 潮流时并行性能的方法[J]. 电网技术，2008，32（13）：15-19.DING Ming，ZHANG Jinbo，WANG Xingqiang. Method for parallel performance enhancement of power flow computation for large-scale power grid by use of preconditioned conjugate gradient method[J]. Power System Technology，2008，32（13）：15-19（in Chinese）.

[4] 徐建亭，王秀英，李兴源. 电力系统电压无功的序列二次规划算法[J]. 电力系统自动化，2001，25（23）：4-7.XU Jianting，WANG Xiuying，LI Xingyuan. Successive quadratic programming method for voltage/reactive power optimization in power systems[J]. Automation of Electric Power Systems，2001，25（23）：4-7（in Chinese）.

[5] 张力平，何大愚，朱太秀. 牛顿法最优潮流与最优无功补偿[J]. 中国电机工程学报，1987，7（1）：11-18.ZHANG Liping，HE Dayu，ZHU Taixiu. Optimal power flow and optimal reactive power compensation by newtons method[J]. Proceedings of the CSEE，1987，7（1）：11-18（in Chinese）.

[6] 柳进，常修猛，柳焯.内点法在偶对潮流优化中的应用[J].电力系统自动化，2007，31（5）：29-33.LIU Jin，CHANG Xiumeng，LIU Zhuo. Application of interior point method in optimization of coupling pair power flow[J]. Automation of Electric Power Systems，2007，31（5）：29-33（in Chinese）.

[7] 刘桂龙，王维庆，张新燕，等. 无功优化算法综述[J]. 电网与清洁能源，2011，27（1）：4-8.LIU Guilong，WANG Weiqing，ZHANG Xinyan，et al.Overview of VAR optimization algorithm[J]. Power System and Clean Energy，2011，27（1）：4-8（in Chinese）.

[8] 刘科研，盛万兴，李运华. 基于改进遗传模拟退火算法的无功优化[J]. 电网技术，2007，31（3）：13-18.LIU Keyan，SHENG Wanxing，LI Yunhua. Research on reactive power optimization based on improved genetic simulated annealing algorithm[J].Power System Technology，2007，31（3）：13-18（in Chinese）.

[9] YOSHIDA H，KAWATA K，FUKUYMA Y. A particle swarm optimization for reactive power & voltage control security assessment[J].IEEE Transactions on Power Systems，2000，15（4）：1232-1239.

[10] 刘科研，盛万兴，李运华. 基于改进免疫遗传算法的无功优化[J]. 电网技术，2007，31（13）：11-16.LIU Keyan，SHENG Wanxing，LI Yunhua. Reactive power optimization based on improved immunity genetic algorithm[J]. Power System Technology，2007，31（13）：11-16（in Chinese）.

[11] 贾德香，程浩忠，马鸿杰. 基于改进禁忌算法的区域控制偏差分区优化方法[J]. 电网技术，2007，31（7）：1-5.JIA Dexiang，CHENG Haozhong，MA Hongjie. Region partitioning optimization of area control error based on improved tabu search algorithm[J]. Power System Technology，2007，31（7）：1-5（in Chinese）.

[12] 邱晓燕，张子健，李兴源. 基于改进遗传内点算法的电网多目标无功优化[J]. 电网技术，2009，33（13）：27-31.QIU Xiaoyan， ZHANG Zijian， LI Xingyuan. Multiobjective reactive power optimization based on improved genetic-interior point algorithm[J]. Power System Technology，2009，33（13）: 27-31（in Chinese）.

[13] 靳丹，王维洲，曹俊龙，等. 基于改进自适应变异概率遗传算法的无功优化方法[J]. 电网技术，2012，31（7）：6-10.JIN Dan，WANG Weizhou，CAO Junlong，et al. Reactive power optimization method based on improved adaptive mutation probability genetic algorithm[J]. Power System Technology，2012，31（7）：6-10（in Chinese）.

[14] 周晓娟，蒋炜华，马丽丽. 基于改进遗传算法的电力系统无功优化[J]. 电力系统保护与控制，2010，38（7）：37-41.ZHOU Xiaojuan，JIANG Weihua，MA Lili. Reactive power planning based on IPM and improved GA hybrid method[J].Power System Protection and Control，2010，38（7）：37-41（in Chinese）.

[15] 崔挺，孙元章，徐箭，等.基于改进小生境遗传算法的电力系统无功优化[J]. 中国电机工程学报，2011，31（19）：43-50.CUI Ting，SUN Yuanzhang，XU Jian，et al.Reactive power optimization of power system based on improved niche genetic algorithm[J]. Proceedings of the CSEE，2011，31（19）: 43-50（in Chinese）.

[16] 何启明，王奔. 基于改进粒子群算法的多目标无功优化[J]. 电网与清洁能源，2009，25（5）：11-14.HE Qiming，WANG Ben. Multiobjective reactive power based on improved particle swarm[J]. Power System and Clean Energy，2009，25（5）：11-14（in Chinese）.

[17] 刘世成，张建华，刘宗岐. 并行自适应粒子群算法在电力系统无功优化中的应用[J]. 电网技术，2012，36（1）：108-112.LIU Shicheng，ZHANG Jianhua，LIU Zongqi. Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization of power system[J]. Power System Technology，2012，36（1）: 108-112（in Chinese）.

[18] HE S，WU Q H，SAUNDERS J R. A novel group search optimizer inspired by anima ecology[C]// IEEE Congress on Evolutionary Computation，2006: 1272-1278.

[19] WU Q H，LU Z，LI M S，et al. Optimal placement of FACTS devices by a group search optimizer with multiple producer[C]// IEEE Congress on Evolutionary Computation，2008：1033-1039.

[20] 宋永超，张勇军，蔡泽祥，等. 一种电力系统无功优化的新型混合优化算法[J]. 电力系统保护与控制，2011，39（24）：16-21.SONG Yongchao，ZHANG Yongjun，CAI Zexiang，et al.A novel hybrid algorithm for reactive-power optimization of power system[J]. Power System Protection and Control，2011，39（24）：16-21（in Chinese）.

[21] 张锋，段余平，邱军，等.基于粒子群算法与内点算法的无功优化研究[J]. 电力系统保护与控制，2010，38（13）：11-16.ZHANG Feng，DUAN Yuping，QIU Jun，et al.Research on reactive power flow based on particle swarm optimizationand interior point method[J]. Power System Protection and Control，2010，38（13）：11-16（in Chinese）.

[22] 杨文翠，陈禄，薛宏波.粒子群和变邻域差分进化搜索算法在多目标无功优化中的应用[J]. 华中电力，2011，24（6）：76-79.YANG Wencui，CHEN Lu，XUE Hongbo. Application of particle swarm and variable neighborhood differiential evolution search algorithm in multi-objective reactive power optimization[J].Central China Electric Power，2011，24（6）：76-79（in Chinese）.

[23] 李娟，杨琳，刘金龙，等. 基于自适应混沌粒子群优化算法的多目标无功优化[J]. 电力系统保护与控制，2011，39（9）：26-31.LI Juan，YANG Lin，LIU Jinlong，et al. Multi-objective reactive power optimization based on adaptive chaos particle swarm optimization algorithm[J]. Power System Protection and Control，2011，39（9）：26-31（in Chinese）.

[24] 曾令全，罗富宝，丁金嫚. 禁忌搜索-粒子群算法在无功优化中的应用[J]. 电网技术，2011，35（7）：129-133.ZENG Lingquan，LUO Fubao，DING Jinman. Application of particle swarm optimization algorithm integrated with tabu search in reactive power optimization[J]. Power System Technology，2011，35（7）: 129-133（in Chinese）.

[25] 张明晔，郭庆来，孙宏斌，等.基于合作博弈的多目标无功电压优化模型及其解法[J]. 电力系统自动化，2012，36（18）：116-121.ZHANG Mingye，GUO Qinglai，SUN Hongbin，et al. A cooperative game throry based multi-objective reactive voltage optimization modle and its solution[J]. Automation of Electric Power Systems，2012，36（18）: 116-121（in Chinese）.

[26] 李鸿鑫，李银红，陈金富，等. 自适应选择进化算法的多目标无功优化方法[J]. 中国电机工程学报，2011，33（10）：71-78.LI Hongxin，LI Yinhong，CHEN Jinfu，et al. Multiple evolutionary algorithms with adaptive selection strategies for multi-objective optimal reactive power flow[J]. Proceedings of the CSEE，2011，33（10）: 71-78（in Chinese）.

[27] 张晓辉，卢志刚，秦四娟. 基于改进细菌群体趋药性算法的电力系统无功优化[J]. 电网技术，2012，36（2）：109-114.ZHANG Xiaohui，LU Zhigang，QIN Sijuan. Reactive power management based on improved bacterial colony chemotaxis algorithm[J]. Power System Technology，2012，36（2）: 109-114（in Chinese）.

[28] 李智，杨洪耕. 一种用于分解协调无功优化的全分邻近中心算法[J]. 中国电机工程学报，2013，33（1）：77-83.LI Zhi，YANG Honggeng. A full decomposition proximal center algorithm for decomposition and coordination of reactive power optimization[J]. Proceedings of the CSEE，2013，33（1）: 77-83（in Chinese）.

[29] 李国庆，杨悦. 基于现代数学算法的配电网动态无功优化研究[J]. 东北电力大学学报，2010，30（4）：26-30.LI Guoqing，YANG Yue. Overview on dynamic reactive power optimization of power distribution network based on modern mathematical algorithms[J]. Journal of Northeast Dianli University，2010，30（4）: 26-30（in Chinese）.

[30] 程彬，刘方，颜伟，等.动态无功优化的混合智能算法[J].重庆大学学报：自然科学版，2007，30（1）：22-27.CHENG Bin，LIU Fang，YAN Wei，et al. Hybrid intelligent method for dynamic reactive power optimization[J]. Journal of Chongqing University：Natural Science Edition，2007，30（1）: 22-27（in Chinese）.

[31] 王韶，张煜成，周鑫，等. 基于一种改进蚁群算法的动态无功优化[J]. 电力系统保护与控制，2012，40（17）：100-109.WANG Shao，ZHANG Yucheng，ZHOU Xin，et al. Dynamic reactive power optimization based on a modified ant colony algorithm[J]. Power System Protection and Control，2012，40（17）：100-109（in Chinese）.

[32] 金立军，张哲，刘源基，等. 于电子式传感器的电力系统故障诊断研究[J]. 高压电器，2011，47（9）: 73-75.JIN Lijun，ZHANG Zhe，LIU Yuanji，et al. Shortcircuit fault diagnos is of power system based on electronic transducer[J]. High Voltage Apparatus，2011，47（9）: 73-75（in Chinese）.

[33] 赖永生，刘明波，陈燕梅. 大规模电网的动态无功优化算法[J]. 电力系统及其自动化学报，2012，24（5）：7-12.LAI Yongsheng，LIU Mingbo，CHEN Yanmei. Algorithm for dynamic reactive power optimization problem in large power grid[J]. Proceedings of the CSU-EPSA，2012，24（5）：7-12（in Chinese）.