基于负荷曲线分布特征的峰谷时段划分和修正策略研究
2014-12-20连振洲温步瀛江岳文
连振洲,温步瀛,江岳文
(福州大学 电气工程与自动化学院,福建 福州 350108)
我国自2003年以来,已大范围普及和推广峰谷分时电价。峰谷分时电价的推行有效地调节了用电峰谷差,对缓解电力紧张局面起到了重要的作用[1]。
峰谷时段的划分和峰谷电价比价关系的确定是制定峰谷分时电价的基础。文献[2]提出用户响应的概念来描述电价对负荷的影响,文献[3-4] 引入电价弹性矩阵,使得用户对峰谷电价的响应得到量化,推动了基于用户响应的峰谷电价研究,特别是为峰谷电价比价关系的研究积累了一定的成果[5-9],甚至出现了一些结合新能源、新技术的电价研究[10-11]。然而由于传统分时表计及其抄表系统的限制,一些地区的时段区间设置长年保持不变。有关峰谷时段划分的理论研究并不多,目前已开展的时段划分方法主要有以下2种。
1)基于供电成本变化分析。文献[12]结合机组运行状况建立发电成本-负荷函数,利用该函数在负荷点的突变特征来划分峰谷时段区间。
2)基于负荷曲线分布分析。文献[13]采用模糊半梯形隶属度函数法,根据负荷曲线上各点分别处于峰时段和谷时段的可能性来划分峰谷时段区间。文献[14]通过分析负荷曲线,采用模糊聚类的方法划分时段,提出考虑用户需求响应的时段划分修正方法。
对比2种时段划分的研究思路,基于负荷曲线分布分析的方法更能发挥峰谷电价引导需求的价格职能,起到价格杠杆作用。模糊隶属度函数法利用负荷曲线的分布特征进行时段划分,但也存在难以合理确定峰谷区间临界点的问题。
本文在此基础上,探讨时段划分的区间界定和修正策略,并以某省4个季度的典型日负荷曲线为例进行峰谷时段划分。考虑不同季度的用电差异性,提出新的全年综合峰谷时段划分模型。
1 峰谷时段初步划分方法
负荷曲线上各时间段处于峰时段或谷时段的可能性采用模糊半梯形隶属度函数来确定[13]。为了方便时段划分,假设典型日负荷曲线上各时段分界点组成的时间点集合为T={t0,t1,t2,…,t23},各时间点对应的负荷值集合为Q={q0,q1,q2,…,q23},通过判断各时间点的负荷值处于峰时段和谷时段的可能性来确定峰、平、谷的时段区间。其中采用偏大型半梯形隶属函数确定各时间点处于峰时段的可能性A(qi),采用偏小型半梯形隶属函数确定负荷曲线上各时间点处于谷时段的可能性B(qi)。
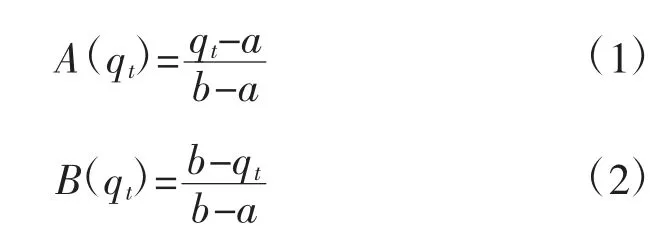
式中,qt为t时间点对应的负荷值;a为各时间点负荷中的最小值;b为各时间点负荷中的最大值。
该方法只需确定负荷曲线上各时间点相对于最高峰段与最低谷段的比值关系,与其具体数值无关。但模糊隶属度函数法需要确定隶属度特征阈值λ,对于不同的λ∈[0,1]可以得到不同的分类。难点在于如何合理确定隶属度特征阈值使得时段划分更加科学。
本文运用集合分类的思想,即不同集合间的样本差异要明显,同一集合内的样本差异应模糊,分别确定偏大型半梯形隶属函数和偏小型半梯形隶属函数的最优阈值λ1和λ2。
设λ1对应峰时段的时间点数量为n1,λ2对应谷时段的时间点数量为n3,平时段的时间点数量为n2=24-n1-n3。峰、平、谷时段区间对应的各时间点负荷集合分别为Q1={p1,p2,…,pn1},Q2={m1,m2,…,mn2},Q3={v1,v2,…,vn3}。为了更好地比较相邻集合间的差距及各个集合内样本间的差异,本文构造阀值指标函数S。
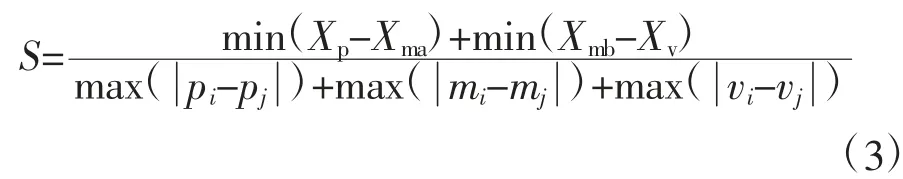
式 中,Xp=min(Q1);Xma=max(Q2);Xmb=min(Q2);Xv=max(Q3);pi、pj为集合Q1内任意2个不同的负荷值;mi、mj为集合Q2内任意2个不同的负荷值;vi、vj为集合Q3内任意2个不同的负荷值。
该函数的分子表征相邻集合之间的最小距离,不同类之间的差异要扩大,即距离越大越好;分母表征集合内样本间的最大差距,同类内样本的差异要缩小,即集合半径越小越好。因此,S越大说明分类越好。
2 峰谷时段划分修正策略
针对模糊隶属度函数法存在部分点根据隶属度特征阀值难以界定时段属性的问题,本文参照已实施的时段划分方案的特点,提出2个修正策略。
1)峰、平、谷时段3个集合的大小不应相差太大,考虑到电力公司和用户的可接受程度,集合内的时间点数量应控制在6~10个。为了提高大发机组的运行效率,高峰时段可以有所缩短,其集合内的时间点数量一般不超过8个。本文通过修正隶属度特征阈值来合理规范峰、平、谷时段集合的大小。
2)在实际应用中,考虑到技术上的可行性和实施的方便,不宜将时段划分得太小,每个时段不应小于2 h[13]。当峰/平/谷集合里的某一个时间点被孤立出来时,可以将其归到相邻时间点所在的集合;或者将其中一个相邻时间点归到孤立时间点所在的集合。具体要根据孤立点及其相邻点对应负荷值的相对大小进行调整。
3 算例分析
3.1 4个季度峰谷时段划分
某省2012年4个季度的典型日负荷曲线如图1所示。
通过分析图1中4个季度的典型日负荷曲线可以得到以下结论:
1)日负荷曲线表现出典型的双峰性,上午和下午一般各出现一次用电高峰,与上午的高峰期相比,下午的高峰时间稍长;而用电低谷通常出现在夜间,时段具有连续性且持续时间较长。
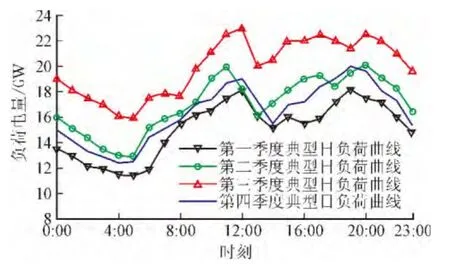
图1 4个季度的典型日负荷曲线Fig. 1 Typical day load curve of four quarters
2)不同季度的负荷用电具有明显的季节性特征,夏季为用电高峰季,比起其他3个季节用电量明显增加;冬季为用电淡季,整体的负荷用电量较其他季节要低。
采用模糊半梯形隶属度函数进行初步划分,运用修正策略进行合理调整后的结果如表1所示。
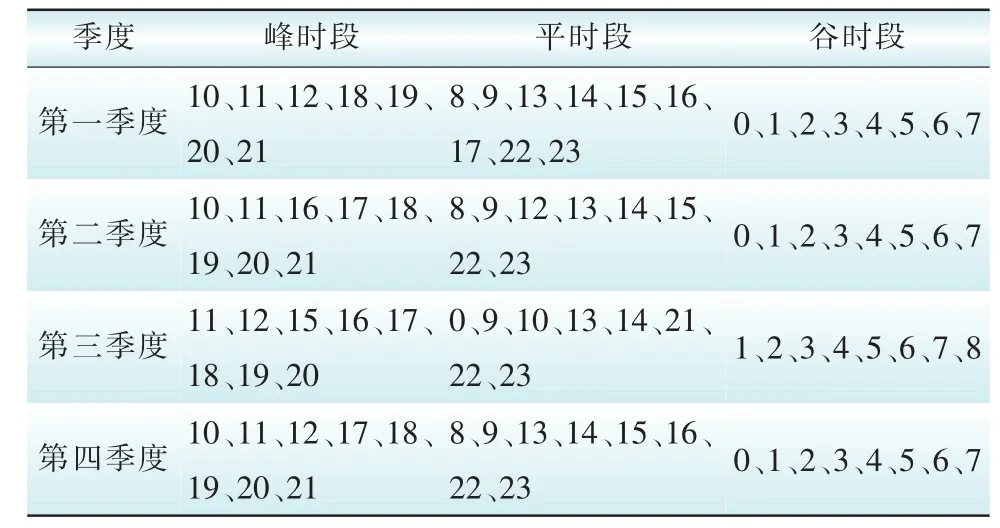
表1 4个季度的时段划分结果Tab. 1 Results of four quarters’time period partition
为了方便统计,本文以时间段起始时刻显示划分结果,如表格中0代表0:00—1:00这一时间段,表2、表3与此同。
3.2 全年综合峰谷时段划分
各个季度用电量占全年用电量的比重不同,其差异应在全年时段划分中得到体现。本文根据各个季度的负荷用电量占全年负荷用电量的比重来确定其对应的权重系数α(i),4个季度的系数之和为1。
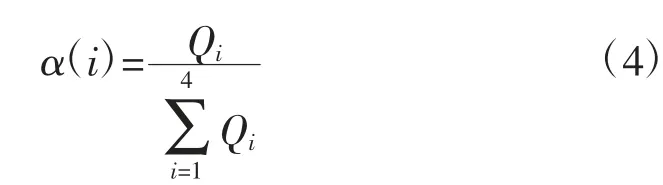
式中,Qi为第i季度典型日的总负荷电量。经过计算可 得α(1)=0.221、α(2)=0.249、α(3)=0.291、α(4)=0.239。
为了兼顾4个季度的用电差异,突出共同特征,本文采用二范数思想,对各个季度负荷用电加权融合,采用时段划分修正策略进行调整,即可建立全年的综合时段划分模型。其中加权二范数函数定义为:
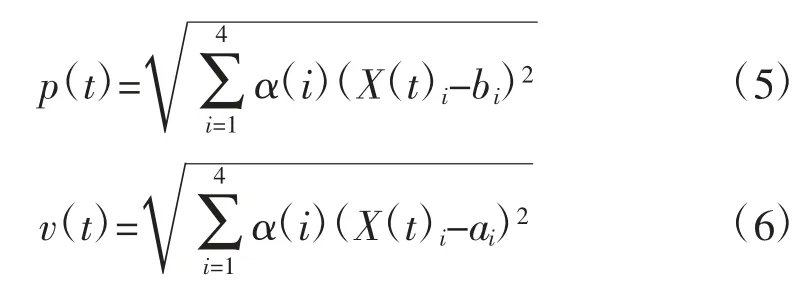
式中,X(t)i为第i季度t时段对应的负荷值;bi为第i季度各时段负荷中的最大值;ai为第i季度各时段负荷中的最小值。
其中公式(5)确定t时段处于峰时段的可能性,p(t)值越小,t时段属于峰时段的可能性越大;公式(6)确定t时段处于谷时段的可能性,v(t)值越小,t时段属于谷时段的可能性越大。
3.3 实例时段划分对比分析
通过对各个季度典型日的负荷电量加权融合,可以得到全年综合典型日负荷柱状图,如图2所示。
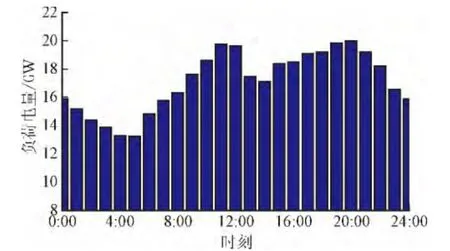
图2 全年综合典型日负荷柱状图Fig. 2 Annual consolidated typical day load histogram
经过公式(5)和公式(6)计算划分并通过修正策略的调整,可以得到全年的综合峰谷时段划分结果,如表2所示。

表2 全年综合时段划分结果Tab. 2 Results of the annual consolidated time period partition
该方案将1天24 h划分为2个峰时段、3个平时段、1个谷时段,总共6个时段,每个时段时间最短2 h,最长8 h。
某省峰谷电价已实施多年,近年来执行的时段划分方案如表3所示。

表3 已实施的时段划分方案Tab. 3 Time period partition scheme implemented
分析图1、图2,对比表2和表3的时段划分可知,本文得到的全年综合时段划分结果更能反映4个季度典型日负荷曲线的峰谷形态特征和变化。具体表现有:12:00—13:00比15:00—16:00更应该划分为高峰期,从图2中可以看出12:00—13:00的平均负荷值要高于15:00—16:00,因此本文的时段划分方案将12:00—13:00归为高峰期,而将15:00—16:00归为平时段,从而更好地激励用户响应削峰;将23:00—0:00归为平时段,而将7:00—8:00归为低谷期,原因是7:00—8:00的平均负荷值要低于23:00—0:00的平均负荷值,调整后低谷特征更加明显。
综上所述,本文的研究方案与已实施方案相比,峰谷时段的划分更合理,更能有效地激励用户的需求响应。2个方案划分结构相似,整体调整幅度较小,可以有效减少调整时段划分后带来的负面社会舆论,易为用户和电力公司所接受。
4 结论
本文针对模糊隶属度函数时段划分方法存在隶属度阀值难以合理确定峰、谷区间临界点的问题,设计阀值指标函数来合理确定时段区间。通过分析已实施峰谷时段划分方案的特征,提出时段划分的修正策略,对一些孤立时间点进行适当调整。
本文依据某省2012年4个季度的典型日负荷曲线进行实例峰谷时段划分,利用阀值指标函数确定时段区间,运用修正策略作适当调整,得出4个季度的划分方案。兼顾各季度的用电特性及比重进行加权融合,采用加权二范数函数法进行划分,得到全年综合时段划分方案,比已实施方案更符合近年来的负荷曲线分布特征,能获得较好的削峰填谷经济效益。
[1] 赵娟,谭忠富,李强. 我国峰谷分时电价的状况分析[J].现代电力,2005,22(2): 82-85.ZHAO Juan,TAN Zhongfu,LI Qiang. Analysis of timeof-use(TOU)power price in China[J]. Modern Electric Power,2005,22(2): 82-85(in Chinese).
[2] 汤玉东,王明飞,吴军基. 基于DSM的分时电价研究[J].电力需求侧管理,2000,2(3): 14-16,19.TANG Yudong,WANG Mingfei,WU Junji. Research on DSM-based TOU[J]. Power Demand Side Management,2000,2(3): 14-16,19(in Chinese).
[3] SHEEN J N,CHEN C S,WANG T Y. Response of large industrial customers to electricity pricing by voluntary time-of-use in taiwan[J]. IEE Proceedings-C,1995,142(2): 157-166.
[4] 秦祯芳,岳顺民,余贻鑫,等. 零售端电力市场中的电量电价弹性矩阵[J]. 电力系统自动化,2004,28(5): 16-19,24.QIN Zhenfang,YUE Shunmin,YU Yixin,et al. Price elasticity matrix of demand in current retail power market[J].Automation of Electric Power Systems,2004,28(5): 16-19,24(in Chinese).
[5] 李晖,康重庆,夏清. 考虑用户满意度的需求侧管理价格决策模型[J]. 电网技术,2004,28(23): 1-6.LI Hui,KANG Chongqing,XIA Qing.Price based decision making for demand side management considering customer satisfaction index[J]. Power System Technology,2004,28(23): 1-6(in Chinese).
[6] 唐捷,任震,胡秀珍. 一种可操作的需求侧管理峰谷分时电价定价方法[J]. 电网技术,2005,29(22): 71-75.TANG Jie,REN Zhen,HU Xiuzhen. An operable peakvalley time-of-use tariff setting method of demand side management[J]. Power System Technology,2005,29(22):71-75(in Chinese).
[7] 丁伟,袁家海,胡兆光. 基于用户价格响应和满意度的峰谷分时电价决策模型[J]. 电力系统自动化,2005,29(20): 10-14.DING Wei,YUAN Jiahai,HU Zhaoguang. Time-of-use price decision model considering users reaction and satisfaction index[J]. Electric Power Automation Equipment,2005,29(20): 10-14(in Chinese).
[8] 袁家海,李蒙,胡兆光. 基于多智能体模拟方法的大用户峰谷电价响应研究[J]. 电网技术,2005,29(23): 44-49.YUAN Jiahai,LI Meng,HU Zhaoguang. Research on large customer response under time-of-use electricity pricing policy based on multi-agent system simulation[J]. Power System Technology,2005,29(23): 44-49(in Chinese).
[9] 郭联哲,谭忠富,李晓军.基于用户响应下的分时电价优化设计模型与方法[J]. 电网技术,2006,30(5): 24-28.GUO Lianzhe,TAN Zhongfu,LI Xiaojun. Demand response based model and method for optimal design of timeof -use electricity price[J]. Power System Technology,2006,30(5): 24-28(in Chinese).
[10] 唐兰兰,温步瀛,江岳文. 考虑风电并网的分时段短期电价预测[J]. 电网与清洁能源,2011,27(12): 84-89.TANG Lanlan,WEN Buying,JIANG Yuewen. Short-term electricity price forecasting based on period-decoupled price sequence with grid-connected wind power[J]. Power System and Clear Energy,2011,27(12): 84-89(in Chinese).
[11] 戴诗容,雷霞,程道卫,等. 电动汽车峰谷分时充放电电价研究[J]. 电网与清洁能源,2013,29(7): 77-82.DAI Shirong,LEI Xia,CHENG Daowei,et al. Study on electric vehicle charging and discharging TOU price[J].Power System and Clear Energy,2013,29(7): 77-82(in Chinese).
[12] 林旻,朱艳卉,胡百林. 基于供电成本的峰谷时段划分及分时电价研究[J]. 华东电力,2005,33(12): 90-91.LIN Min,ZHU Yanhui,HU Bailin. Peak and valley periods division and time-of-use price based on power generation cost[J]. East China Electric Power,2005,33(12): 90-91(in Chinese).
[13] 丁宁,吴军基,邹云.基于DSM的峰谷时段划分及分时电价研究[J]. 电力系统自动化,2001,25(23): 9-12,16.DING Ning,WU Junji,ZOU Yun. Research of peak and valley time period partition approach and TOU price on DSM[J]. Automation of Electric Power Systems,2001,25(23): 9-12,16(in Chinese).
[14] 程瑜,翟娜娜. 基于用户响应的分时电价时段划分[J].电力系统自动化,2012,36(9): 42-46.CHENG Yu,ZHAI Nana. Electricity price peak and valley periods division based on customer respons[J]. Electric Power Automation Equipment,2012,36(9): 42-46(in Chinese).
