珠磨机减速器单臂行星架的结构优化设计

潘月仙，邹 旻

PAN Yue-xian, ZOU Min

(常州大学 机械工程学院，常州 213016)

0 引言

行星架作为行星减速器的重要部件，承担着输出运动和动力的重任，它的结构对所在减速器的工作性能，如整个机构的承载能力、行星轮间的载荷分配、受载变形量以及运行时的振动和噪音等都有着重要的影响。为了加工和拆装方便，珠磨机减速器行星轮轴多采用单臂行星架结构，如图1所示。这种结构与双臂式行星架相比，虽然具有轴向尺寸小、质量轻，装配方便等优点，但受力情况和刚度不如双臂行星架，容易使行星轮轴偏载。本文采用ANSYS软件对其进行分析，并进一步对单臂式行星架进行结构上的优化设计，得出更加合理的行星架结构。

1 行星架有限元分析

1.1 行星架有限元模型的建立

以图1所示行星架为例建模，它由行星架主体和耳轴通过内六角圆柱头螺钉联接而成。运用Pro/E软件的建模功能得到行星架的三维实体模型，通过设置Pro/E和ANSYS软件之间的接口，将ANSYS直接集成在Pro/E中，省略了将所建模型保存为IGES格式文件再进行导入、导出的步骤，可以直接在Pro/E建模的激活窗口中进行数据转换，直接启动ANSYS软件。这种方法减少了数据的转存工作，既节省了时间，也可保证结果的精确性。同时对模型进行适当的简化，这样能在不影响计算结果的前提下，提高计算效率。得到的有限元模型如图2所示。

行星架主体材料为40 Cr，弹性模量为206GPa，泊松比为0.28[1]，选用SOLID92作为行星架网格单元，对有限元模型进行智能化网格划分。

图1 行星架结构简图

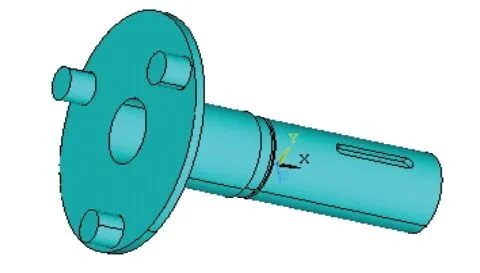
图2 行星架有限元模型

1.2 模型载荷和边界条件的确定

1)行星架轮轴受载分析

在对行星架模型施加载荷之前首先要知道行星架的受力情况[2]，在如图3所示的行星传动系统中，太阳轮带动行星轮运动，行星轮带动行星轴转动，又因为行星轮轴同行星架是一体的，进而带动了整个行星架的运动，所以对行星架进行受力分析，只需要计算行星轮轴的受力即可，行星轮轴的受力[3]如下图4所示。

图3 行星传动简图

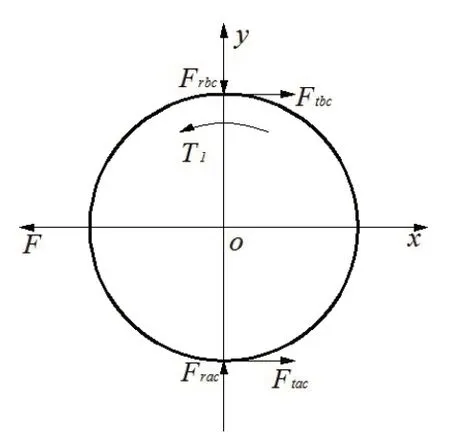
图4 行星轮轴简化受力图

式中：Ftac，Ftbc分别为太阳轮和内齿轮对行星轮的圆周力；Frac，Frbc分别为太阳轮和内齿轮对行星轮的径向力；Tc，Ta分别为行星轮和太阳轮所受转矩；dc，da分别为行星轮和太阳轮分度圆直径；Zc，Za分别为行星轮和太阳轮齿数；m为模数；np为行星轮个数。

将上述得到的力以集中载荷的形式施加在3个行星轮轴的形心处，并沿着圆周的切线方向，可以通过在轮轴的形心处建立硬点再施加载荷[4]。

2)键槽受载分析

一般行星架末端是通过内花键来传递转矩带动低速轴转动，本文的行星架所在的减速器是采取立式形式进行工作，输出轴较长，输出转矩是通过键来传递，因而也要对键槽进行受力分析，计算键槽上的载荷[5]。

工作面上的压力为：

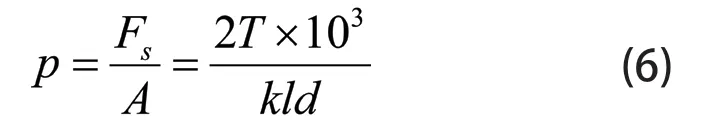
式中：Fs为剪力；A为受载面积；T为行星架传递转矩；k为键与轮毂键槽的接触高度；l为键的工作长度；d为轴的直径。

3)边界条件的约束

对行星架端部处的轴承施加全约束。

1.3 有限元分析结果

给出关于该单臂行星架计算分析时一些条件数据：输入件传递的功率为，输入件的转速n=730r/min，传动比为，行星轮个数为np=3，齿轮模数m=3，太阳轮齿数为。行星架输出壁厚为10mm，圆头平键的工作长度，键与轮毂键槽的接触高度，行星架输出轴的直径。

对单臂行星架有限元模型进行求解，得出行星架的应力分布和变形云图分布如图5和图6所示。

图5 应力分布云图

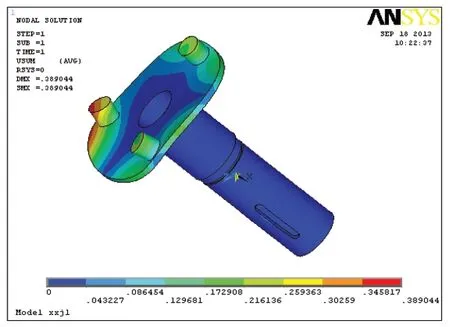
图6 变形云图

从行星架的应力分布云图和变形云图上来看，单臂行星架受力后变形比较大，尤其是在轮轴处应力和变形都比较大，最大应力为420.256Mpa，最大变形量达到0.389044mm。行星架轮轴变形时会使齿轮在运转时发生偏载，直接影响齿轮的接触强度和弯曲强度，甚至造成轮齿断裂等安全事故，大大缩短了减速器的使用寿命，因而很有必要对行星架结构和尺寸进行优化改进，改善其强度和刚度，减小变形量和应力，同时在质量方面尽量不增加。

2 行星架的结构优化设计

2.1 结构上的改进优化

由于考虑到单臂行星架的受力情况，如果单提高行星架的壁厚，虽然可以适当的减小变形量和应力，但是当壁厚的厚度超过一定的值时，应力反而没有减小许多。而且提高行星架壁厚也会带来质量的增加，尺寸也不一定能适合箱体。因此提出一种实用新型的单臂式行星架装置，该装置包括行星架和轮轴盖板，行星架上设有行星轮轴，并且采用行星架与行星轮轴整体成型的的方式；行星轮轴的悬臂端上设有定位安装孔和螺纹孔，轮轴盖板上设有带中心孔的定位安装凸台；盖板上的定位安装凸台插入行星轮轴上的的定位安装孔内，固紧螺钉穿过中心孔将盖板固紧在行星轮轴上，使得盖板和行星架连成一体；定位安装凸台的厚度与轮轴盖板厚度大致相同；定位凸台与定位安装孔之间采用基孔制过渡配合。该行星架的结构如图7所示。

图7 改进后的行星架组件

改进后的行星架结构兼具了双臂整体式行星架的优点，而且改进的后的行星架拆装比双臂式的方便，制造容易，而且轮轴盖板的厚度也不需要太厚，质量上增加的不多。

采用与上述相同的加载和约束方式，进行有限元分析，应力分布云图和变形云图分析结果分别如图8和图9所示。

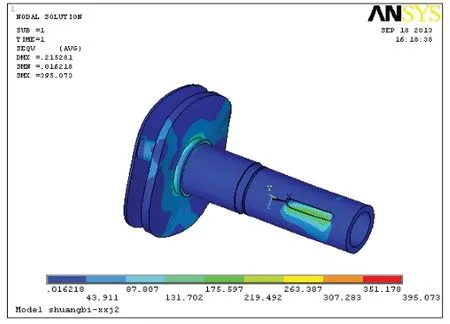
图8 应力云图

图9 变形云图

从改进后的行星架应力云图和变形云图来看，行星架的最大变形量为0.215281mm，比之前降低了44.79%，行星架轮轴的根部处采用了圆弧过渡，行星架的最大应力也相应的下降了不少。为了找出行星架改进后尺寸的最优方案，在其他尺寸条件不变的情况下，得到轮轴盖板厚度和行星架输出臂厚的最优值，列出了几种方案进行对比。原单臂行星架壁厚为10mm，最大应力为420.256Mpa，最大变形量达到0.389044mm。改进的行星架轮轴盖板厚度大约取行星架壁厚的1/3，可以适当地对两者厚度进行调整，进行计算分析，如表1所示。

表1 方案对比表

从上表中数据分析得出，当在轮轴盖板厚度取5mm，行星架输出壁厚取13mm时，行星架的最大应力和最大变形量比较小。

由于改进后的行星架与轮轴整体成型，并且在轮轴的齿根处采用圆弧过渡，使得根部处的受力情况得到很大提高。分别计算齿根处的不同的圆角半径对应的应力值，如图10所示为半径应力变化曲线图。

图10 半径-应力变化图

从图中应力变化曲线可以看出，随着齿根处圆角半径的增大，齿根处的应力值逐渐减小，但是圆角半径增大到一定值时，应力值就趋于不变了。因而在实际运用中，需要选择合适的过渡圆角，从而能减小齿根处的应力。如上述改进的行星架齿根处的圆角半径再适当增大，应力值和最大变形量必然还会下降，行星架安全可靠度也会提升。

2.2 质量上的改进优化

考虑到上述单臂行星架改进后虽然在强度上有大幅提高，但是在质量上或多或少都是增加了，同时也观察到在行星架结构中，行星轮轴之间的地方没有利用，因此有改进之处。该行星架的行星轮轴个数为3个，行星轮轴构成的是外形是三角形，因而提出将圆形的双臂结构改为三角形结构，可以适当的切除边缘壁板，进而能减轻行星架的质量，结构如图11所示。若行星架有4个或4个以上行星轮轴，可以不考虑改进，因为外形变化后质量下降的并不是很多，所以直接可以用圆形代替。

图11 三角形单臂行星架组件

对这种三角形单臂行星架进行有限元分析，应力云图和变形云图分别如图12和图13。

从上图中分析得到，改为三角形臂行星架后，其最大变形量为0.232519mm，比原先最初的单臂行星架的变形量下降了40.23%，最大应力值为385.339Mpa，比之前的下降了8.25%。同时，行星架的质量也比之前下降11.8%，因此改进后的行星架在刚度、尺寸、质量方面达到了一个优化，并且加工简单，装配方便。

图12 三角形单臂行星架组件应力云图

图13 三角形单臂行星架组件变形云图

3 结论

通过对单臂行星架进行有限元分析，对其进行结构上的改进，改进后的行星架兼具了双臂行星架的优点，不仅有着轴向尺寸小、质量轻，装配方便等优点，在强度和刚度上有大幅提高，同时行星架的变形量也有明显的下降，并且拆装方便，加工简单，提高了珠磨机减速器的可靠性，延长了减速器的使用寿命，具有重要的意义，这对于之后行星传动系统的设计，具有一定的参考价值。

[1]徐灏.机械设计手册(第2版)[M].北京：机械工业出版社,2003.

[2]焦映厚,陈照波,付龙,等.大型立式齿轮箱行星齿轮传动系统的优化设计[J].机械传动,2012,36(6)：58-64.

[3]渐开线齿轮行星传动的设计与制造编委会.渐开线齿轮行星传动的设计与制造[M].北京：机械工业出版社,2002.

[4]赵丽娟,陈令国,刘红梅.矿用减速器行星架的有限元分析[J].煤矿机械,2007,28(1)：51-52.

[5]卢洋,刘静娜.基于ANSYS的键联接有限元分析[J].机电产品开发与创新,2010,23(5)：78-80.

[6]饶振刚.行星齿轮传动设计[M].北京：化学工业出版社,2003.

[7]刘鸿文.材料力学[M].北京：高等教育出版社,2004.

[8]谢龙汉,刘新让,刘文超.ANSYS结构及动力学分析[M].北京：电子工业出版社,2012.