基于切换多胞模型的变体飞行器增益调参控制

王 通 王 青

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

江未来 董朝阳

(北京航空航天大学 航空科学与工程学院，北京100191)

变体飞行器是一类外形结构可随飞行任务或外部环境变化的新型飞行器，其常见的变形形式包括鸭翼伸缩、后掠角改变、机翼折叠等，从而保证变形前后在不同任务模式下均满足飞行性能要求.作为一种新概念飞行器，变体飞行器有望成为现代高性能飞行器实现突破发展的源泉，具有重要的研究价值和广阔的应用前景.

飞行过程中的外形变化会引起质心位置、转动惯量、翼展与面积等多种构型参数的变化，还会引起气动力和惯性力的非线性变化，给飞行器的气动、结构和控制等学科提出了一系列具有挑战的研究课题［1－4］.在变体飞行器姿态控制系统设计方面，如何建立数学模型准确反映对象的变形特性，并确保快速变形时大包线下的飞行稳定和控制性能成为亟待解决的关键问题.

文献［5］针对一类机翼形态可变的飞行器进行了多体动力学建模，建立了变体飞行器变形过程中的6自由度非线性动力学方程.文献［6］针对变体飞行器的不同形态设计了相应的模型跟踪控制器以保证在不同的飞行状态都保持优化的飞行性能.但是现有文献均未从理论上保证变体飞行器在大包线下快速变形时的飞行稳定性.

本文针对一类后掠翼可变的飞行器，建立了基于切换多胞系统的变体飞行器模型，提出了保证三维包线下飞行稳定的控制综合方法，仿真结果表明在快速变形的情况下，所给的控制方案满足系统的稳定性和跟踪性能要求.

1 变体飞行器建模

变体无人机Fire-Bee是美国新一代航空公司设计的一款变体无人技术验证机，其在飞行过程中能够在“巡航”和“高速”两种形态间进行变形，如图1所示.

图1 变体飞行器形态示意图

变体无人机Fire-Bee的机翼后掠角χ的变化范围是15°～60°，平均气动弦长、展长和机翼面积等参量随后掠角连续变化，重心位置可通过机身的配重自动调整.表1列出了变体飞行器在“巡航”和“高速”两种形态下的构型参数，其他后掠角度对应的参数可通过拟合得到，完整的气动数据表可参考文献［7］，易知变体飞行器的气动参数都是后掠角χ的函数.这里给出变体飞行器Fire-Bee的纵向短周期非线性动力学模型:式中，VT为飞行速度;α为攻角;q为俯仰角速率;Ma为马赫数;H为高度;¯q为动压;δe为升降舵偏角;CL，Cm分别为升力系数和俯仰力矩系数，其他参数的物理意义参见表1［8］.

表1 变体飞行器构型参数

在系统平衡状态对式(1)进行线性化，得到线性化小扰动状态空间模型:

式中，状态变量 x=(Δα，Δq)T;控制变量 u为δe;Zα，¯Mα，¯M˙α，¯Mq，Zδe，¯Mδe均为动力学导数.系统矩阵和控制矩阵可由变体飞行器当前的气动参数和构型参数计算得出，故可近似为高度、马赫数和后掠角的函数.

变体飞行器在以高度、马赫数和后掠角为参量的三维包线下，系统模型随气动参数和构型参数具有渐变特性，可视为如下的线性切换系统:

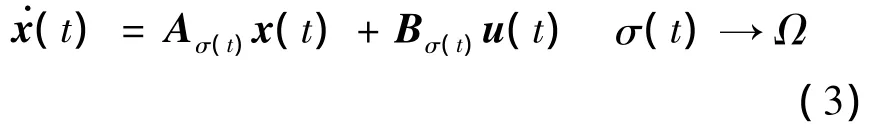
式中，Ω为三维飞行包线内工作点的有限集合;σ(t)为切换律.系统根据当前的高度、马赫数和后掠角决定所处的工作点并切换至相应的子系统下.进一步可将其等价为具有局部重叠特性的若干个切换子系统［9］:

各个切换子系统的形式如下:

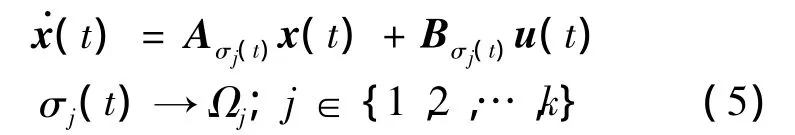
式(5)中的每个切换子系统可对应为一个多胞系统，该多胞系统的顶点即为各切换子系统的切换状态，在三维包线下体现为各设计点，得到如下所示的切换多胞系统:

2 设计点选取

传统的增益调参控制器综合过程一般采用线性插值方法，所得的控制器无法从理论上保证全包线飞行的稳定性.本文在前述变体飞行器切换多胞模型的基础上，将控制系统分解为多胞系统顶点(即单个设计点)的反馈增益设计和全包线下的控制器综合.前者可有效继承传统的线性控制设计方法，后者则通过切换系统稳定性理论和特殊的插值方法保证变体飞行器在全包线飞行过程中的稳定性.

对传统的飞行包线进行拓展，将以高度和马赫数为坐标的二维包线拓展为以高度、马赫数和后掠角为坐标的三维包线.在飞行包线内选取若干设计点，变体飞行器在这些设计点上可以近似为线性模型.设计点的数量应当适中，既要满足包线内动特性描述的需要，还要减少设计工作量，同时为后续的稳定性分析提供基础.

在变体飞行器的三维包线内，遍历高度3，6，9，12，15，18 km，马赫数 0.2，0.5，1.0，1.5，2.0，后掠角 15°，30°，40°，50°，60°的所有组合，得到原始的150个设计点.进一步考虑变体飞行器的任务模式，当其处于不同形态时，飞行高度和马赫数具有一定的自然约束，即“巡航”形态适用于中低空域、低速飞行状态，而“高速”形态适用于中高空域、高速飞行状态.因此有必要剔除与任务模式相悖的设计点，得到83个符合飞行任务要求的设计点.文献［10］基于折叠翼飞行器的LPV模型，利用小凸包算法研究了设计点的选取方法，本文运用小凸包算法对上述83个设计点计算其三维空间中的凸包包络点，作为切换多胞系统的顶点，共计18个，设计点筛选结果如表2所示.

表2 设计点筛选

针对所选择的18个设计点，采用线性二次型最优控制方法设计单点控制器，各设计点的状态反馈增益向量如表3所示.

表3 设计点处的状态反馈增益向量

3 控制器综合

3.1 插值方法

基于选取的18个设计点建立变体飞行器的多胞系统模型，按照设计点将飞行包线分割成有限个长方体，长方体各顶点均为18个设计点中的点，且各长方体内部不包含其它设计点，则飞行包线内任意状态点处的线性模型均通过式(7)表示为某长方体内状态点处的线性小扰动方程.

式中(Ai，Bi)是长方体各顶点处的系统矩阵与输入矩阵.由式(7)可知，长方体内状态点处的线性小扰动模型由8个设计点处的线性小扰动模型经过线性加权确定.如图2所示，针对长方体内的某状态点P，ρi由式(8)计算得到.

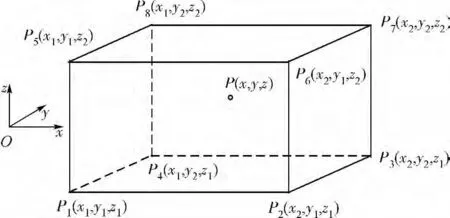
图2 多胞模型加权系数计算示意图

图2和式(9)中的x，y，z分别代表三维飞行包线中的相应坐标，式(8)和式(9)用以完成长方体内的插值计算.

进一步，变体飞行器切换多胞系统建模下全包线下工作点处的控制器可通过式(10)的插值方法得到.

式中，X+为X的M-P伪逆;ki为长方体各顶点处的状态反馈增益向量.该插值方法不同于传统的线性插值，它能够在一定条件下保证变体飞行器的全包线飞行稳定性，稳定性分析方法将在第3.2节中进行详细介绍.

3.2 稳定性分析

下面以定理的形式给出第3.1节控制器插值得到的变体飞行器闭环系统的全包线稳定性分析方法.

定理1 针对形如式(6)的变体飞行器切换多胞模型所有设计点设计状态反馈控制器u=－kix，如果存在正定矩阵P使得下列线性矩阵不等式组成立:

并按照式(12)对长方体内的任意状态点进行状态反馈控制器插值:

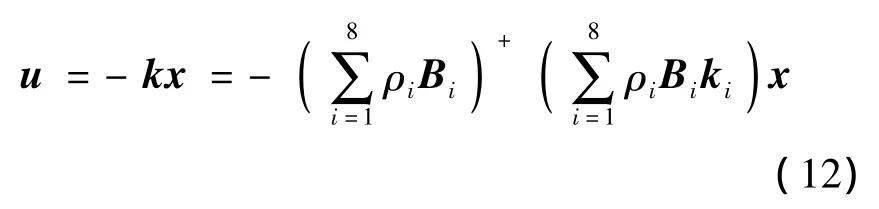
则可保证变体飞行器全包线飞行稳定.

证明 由定理易知，长方体的8个顶点构成的切换子系统:

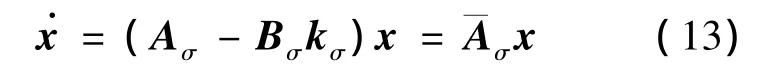
满足以下不等式组:

对于长方体内的任意状态点，则有

又因为

易知长方体内的状态点与长方体的顶点具有公共Lyapunov函数V=xTPx，也即在长方体内的飞行可以确保稳定性.

由于三维飞行包线内的所有设计点均具有公共Lyapunov函数，因此不同长方体内的任意状态点均具有公共Lyapunov函数V=xTPx，则在全包线内均可以确保飞行稳定.证毕

4 仿真验证

经过验证，所选取的18个设计点的线性模型在加入最优状态反馈后具有公共Lyapunov函数，可以通过第3.1节所述的插值方法得到保证全包线下稳定的控制器.

考虑变体飞行器的后掠角χ在15 s内由60°变为15°，即以 －3(°)/s的后掠角变化率由“高速”形态向“巡航”形态变形并且位于第2节所讨论的三维飞行包线内部.

在相应的攻角指令下，系统的仿真结果如图3～图5所示.

图3 攻角响应曲线

由以上仿真曲线可见，攻角响应曲线能够较好地跟踪攻角指令，且受机体变形过程的干扰较小;俯仰角速率波动幅度在2(°)/s以内，舵偏角幅值也在合理的范围内.仿真结果表明所设计的全包线控制综合方法在保证飞行稳定性的同时，也具有较好的控制性能.

图4 俯仰角速率响应曲线

图5 舵偏响应曲线

5 结 束 语

研究了可变后掠翼变体飞行器的全包线控制器设计与综合方法，在非线性模型的基础上建立了基于切换多胞系统的变体飞行器模型，利用小凸包算法从三维飞行包线中选取了数量适中的设计点，并对各设计点处的线性化模型设计了最优控制律.提出了一种新的控制器插值方法完成变体飞行器三维包线下的控制综合，从理论上保证了变体飞行器的全包线稳定性，也继承了传统增益调参方法的优势，具有良好的控制效果.

References)

［1］Chakravarthy A，Grant D T，Lind R.Time-varying dynamics of a micro air vehicle with variable-sweep morphing［J］.Journal of Guidance，Control，and Dynamics，2012，35(3):890 － 903

［2］Seigler T M，Neal D A.Analysis of transition stability for morphing aircraft［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1947 －1953

［3］乐挺，王立新，艾俊强.变体飞机设计的主要关键技术［J］.飞行力学，2009，27(5):6 －10 Yue Ting，Wang Lixin，Ai Junqiang.Key technologies in morphing aircraft design［J］.Flight Dynamics，2009，27(5):6 － 10(in Chinese)

［4］陆宇平，何真.变体飞行器控制系统综述［J］.航空学报，2009，30(10):1906 －1911 Lu Yuping，He Zhen.A survey of morphing aircraft control systems［J］.Acta Aeronautica et Astronautica Sinica，2009，30(10):1906－1911(in Chinese)

［5］Obradovic B，Subbarao K.Modeling of flight dynamics of morphing wing aircraft［J］.Journal of Aircraft，2011，48(2):391 － 402

［6］Abdulrahi M.Maneuvering control and configuration adaptation of a biologically inspired morphing aircraft［D］.Florida:University of Florida，2007

［7］Seigler T M.Dynamics and control of morphing aircraft［D］.Virginia:Virginia Polytechnic Institute and State University，2005

［8］苏铁，董朝阳，侯砚泽.变体无人机动力学模型及切换控制研究［J］.沈阳航空航天大学学报，2012，29(1):1 －5 Su Tie，Dong Chaoyang，Hou Yanze.Modeling and switching control of morphing UAV［J］.Journal of Shenyang Aerospace University，2012，29(1):1 －5(in Chinese)

［9］Hou Yanze，Wang Qing，Dong Chaoyang.Gain scheduled control:switched polytopic system approach［J］.Journal of Guidance，Control，and Dynamics，2011，34(2):623 －629

［10］Baldelli D H，Lee D，Pena R S，et al.Modeling and control of an aeroelastic morphing vehicle［J］.Journal of Guidance，Control and Dynamics，2008，31(6):1687 －1699