一种模拟滤波电路数字化方法
2014-12-18何亚杰
何亚杰
(西安电子科技大学CAD研究所,陕西西安 710071)
随着信息科技的发展,信号处理得到了大幅推动,已经被广泛应用于雷达、通信、自动化、航空航天等领域。在信号处理系统中,输入信号通常含有各种噪声和干扰。为对信号进行准确的测量和控制,必须削弱或滤除被测信号中的噪声和干扰。一般在系统中可选用硬件滤波和软件滤波。硬件滤波又分为无源滤波和有源滤波,无源滤波是通过RC滤波器或LC滤波器等模拟滤波器进行滤波。软件滤波也称数字滤波,是通过一定的算法削弱噪声的影响。硬件滤波的优势是不需要进行复杂的程序处理,反应灵敏。而软件滤波的优势是不需要硬件的投入,而且可靠稳定。
综合两者的优势,本文提出了一种以低通二阶RC无源滤波电路为基准,用Matlab和Visual C++设计一个具有相同功能数字滤波器的方法即模拟电路数字化方法,以滤除信号中的高频杂波,得到了较为理想的波形。
1 模拟电路数字化方法
模拟电路数字化的过程如下,首先从硬件滤波电路出发,计算电路的传递函数H(s)。由于软件滤波的信号是离散的数字信号,所以将H(s)转换成离散域的H(z),通过Matlab编程实现对信号的滤波。如果滤波效果不理想,则对传递函数中的参数进行调整,得到具有较理想滤波效果的H(z)。为最终用Visual C++编程实现,需要将H(z)反变换得时域的h(t),与信号进行卷积和运算以完成滤波。经过以上步骤,完成模拟滤波电路数字化的过程,并在Matlab和Visual C++平台上实现滤波。
2 二阶RC无源低通滤波电路
对于模拟电路的分析,通常采用传递函数的分析方法。电子电路往往是由若干个动态环节连在一起构成一个复杂电路。对于每个具体环节来说,都有它的输入量和输出量,而一定输入量的变化都会引起输出量的变化。根据一个环节中所进行的物理过程可以写出微分方程,它表示了该环节输出量和输入量的关系。
例如RLC振荡回路的微分方程为
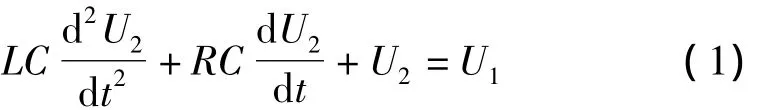
输入量与输出量都是时间t的函数,用微分方程直接表示输入量与输出量时间函数之间的关系比较复杂。但利用拉氏变换把时间函数变换为s的函数以后,原函数对于时间t的微分积分就简化为s的乘除法。
在零起始条件下,一个动态环节的输出量的拉氏变换用X(s)表示,输入量的拉氏变换用F(s)表示,把称为传递函数。
通常信号在进行放大之前,先对该信号进行滤波。以低频信号为例,使用经典的二阶RC无源滤波电路进行滤波,电路如图1所示。在接下来的部分将以此电路为例对模拟电路数字化方法进行详细的分析和讲解。
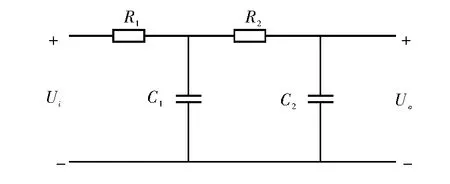
图1 二阶RC无源滤波电路
计算出该电路的传递函数H(s)如式(2)所示。其中,b=R1C1+R1C2+R2C2,a=R1R2C1C2。
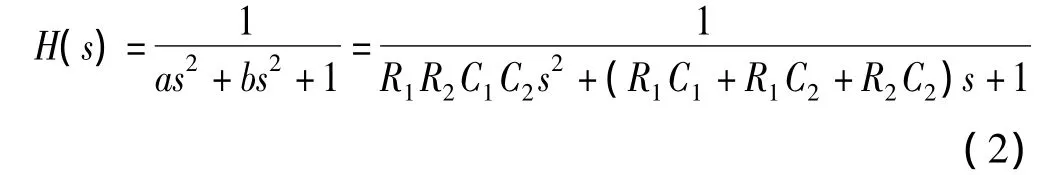
3 传递函数离散化
滤波器的滤波效果与R1、R2、C1和C2等参数相关,如果取值不当会造成滤波效果不理想。对于复杂的传递函数,谐振频率和带宽不易计算,所以本文采用控制变量法。
对于多因素的问题,常常采用控制因素的方法,把多因素的问题变成多个单因素的问题。每一次只改变其中的某一个因素,而控制其余几个因素不变,从而研究被改变的这个因素对事物的影响,分别加以研究,最后再综合解决,这种方法叫控制变量法,被广泛地运用在各种科学研究之中。
得到传递函数后,就可以对信号进行滤波。由于待处理的数据是数字信号,若想仿真需将频域的传递函数转换为z域的传递函数,即将模拟滤波器转换为数字滤波器。模拟滤波器转换为数字滤波器有两种方法:脉冲响应不变法和双线性变换法。
脉冲响应不变法是一个稳定的设计,主要用于设计某些要求在时域上能模仿模拟滤波器功能的数字滤波器。这种变换法的主要特点是频率坐标的变换是线性的,即由于混叠现象,阻带边缘的衰减要比模拟滤波器稍差一些,但仍能满足技术指标的要求。脉冲响应不变法要求该模拟滤波器是带通滤波器或者低通滤波器,但这种方法在阻带没有起伏的情况下才有用。
双线性变换法映射也是一种稳定的设计,不存在混叠现象,对能够变换的滤波器类型没有限制。但这种方法也有固有缺陷:模拟频率和数字频率之间是非线性关系,它使得频率的标度弯曲,不能保持原来的模拟滤波器的相频特性;数字的频率响应与模拟的频率响应有明显的差别。一般情况下,可以通过频率的预畸变进行校正。但总体来说,双线性变换法的仿真结果比脉冲响应不变法更加理想。
由于脉冲响应不变法从s平面到z平面是多值映射,会在频域响应产生混叠失真。而双线性变换法可以把整个s平面变换到整个z平面上去,且使s的左半平面映射到z平面的单位圆内,所以设计采用双线性变换法[7]。
双线性变化法的映射函数为

将该映射式(3)代入式(2),可得拉普拉斯域的传递函数H(z)如式(4)所示。其中f=1/T,A=4af2+2bf+1,B=8af2-2,C=4af2-2bf+1。
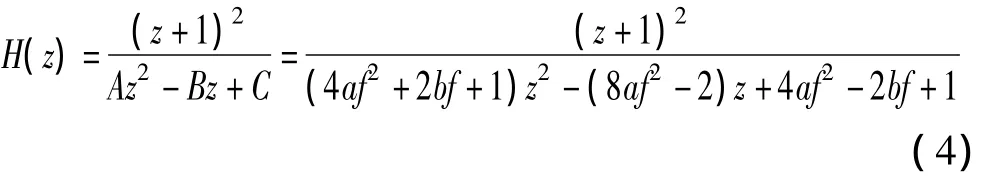
调用Matlab中的Filter函数R1和R2调节参数、进行仿真,仿真结果如图2所示。图2(a)是未加滤波的波形,图2(b)、图2(c)、图2(d)的电阻依次增大,从图中可以看到,电阻越大,高频分量越少。
4 时域传递函数
Matlab一般只用于功能仿真,而实际项目应用,通常采用Visual C++软件编程进行信号控制和硬件实现,所以需要将Matlab仿真时使用的滤波器函数Filter转化为C代码实现。
软件编程有时域和频域两种思路。由于输入信号较为复杂不易进行时-频转换,只能采用时域滤波。所以需将传递函数反变换到时域,对信号进行滤波处理。
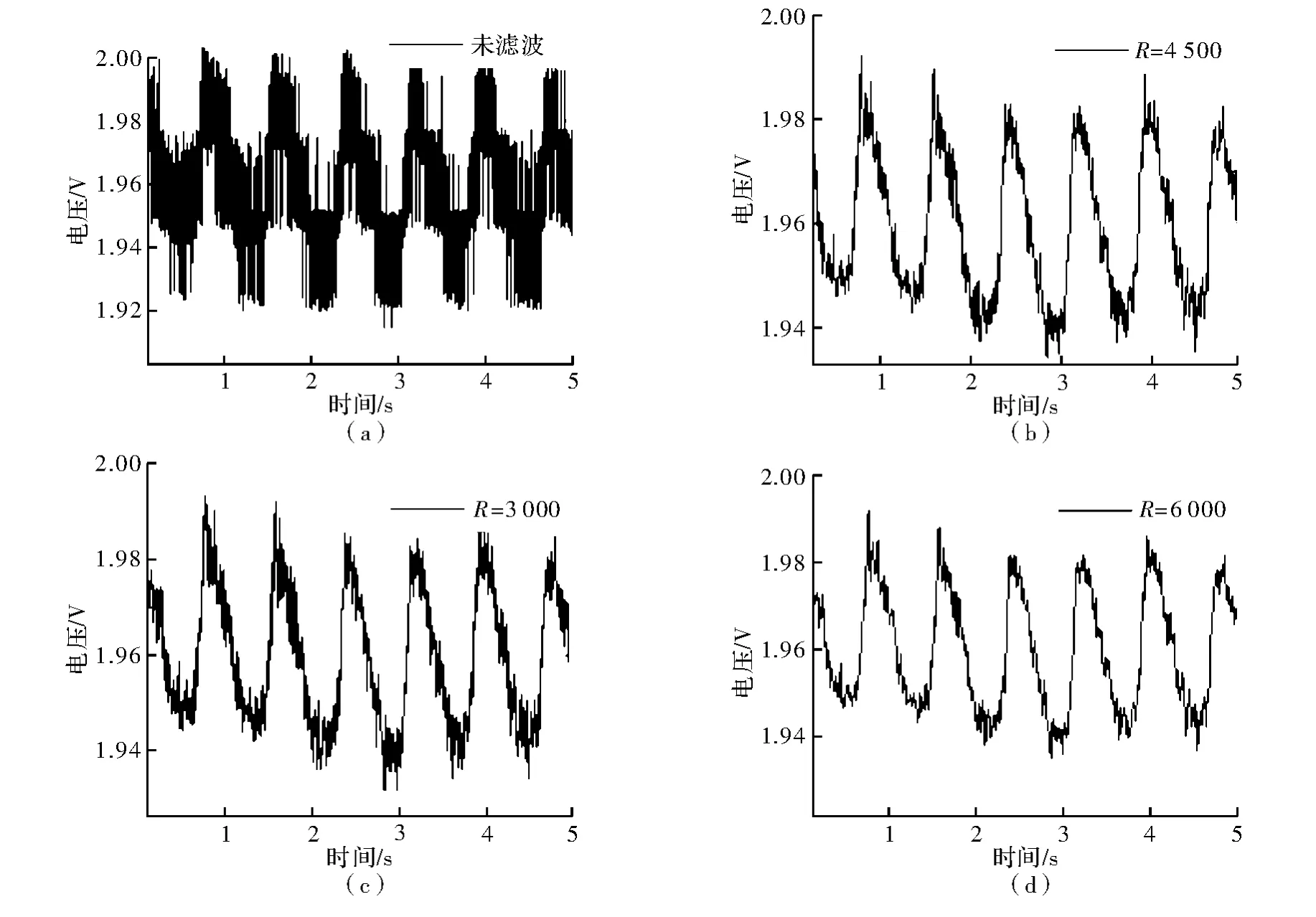
图2 调节R滤波仿真图
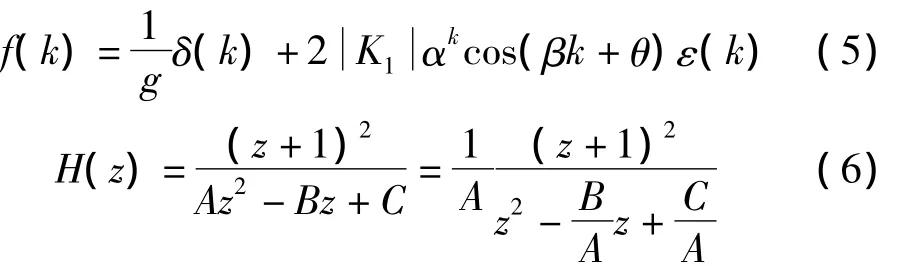
由于进行卷积运算时传递函数需要翻转,可推出h(k)的表达式如式(7)所示

5 时域卷积滤波
卷积在通信技术和信号处理中起着重要的作用。在线性时域系统中,根据时间的连续性,可以分为卷积积分和卷积和。在LTI连续时间系统中,把激励信号分解为一系列冲激函数,求出各种冲激函数单独作用于系统时的冲激响应,然后将这些响应相加就得到系统对于该激励信号的零状态响应。这个相加的过程表现为求卷积积分。在LTI离散系统中,可用上述方法进行分析。由于离散信号本身是一个序列,因此,激励信号分解为单位序列的工作就较容易完成。如果系统的单位序列响应为已知,那么,也不难求得每个单位序列单独作用于系统的响应。把这些序列相加就得到系统对于该激励信号的零状态响应,这个相加的过程表现为求卷积和。
由于本系统中的信号是离散时间序列,常用的卷积和的求解方法有图解法、对位相乘求和法、解析法和列表法等4种。一般,待处理的信号的数据量比较大,列表法不适用,所以采用解析法。
卷积与傅里叶变换有着密切的关系。利用两个函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换的性质,能使傅里叶分析中许多问题的处理得到简化。本文正是采用这一点,将频域的滤波转化为时域滤波。
频域相乘等效于时域卷积。编写C程序求输入信号和传递函数的卷积和。当两个信号为因果信号时,可以根据式(5)求卷积和。当f1(k)的数据长度为m;f2(k)的数据长度为n(n<m)时;需将f2(k)补零将长度扩充为 m;所得 f(k)的数据长度为2m-1,注意f(m)之后的数据是以前数据效果的残留,为无效数据可省略,最终f(k)的有效数据长度为m。
6 结果及分析
信号分别经卷积和滤波和Filter函数滤波,将滤波后的数据导入Matlab比较,结果如图3所示。由图可见,前者在初始状态出现尖峰,这是因为卷积和是在特定窗口内时域累加的过程,会造成头部数据和尾部数据不准确。虽然编写的C卷积和滤波程序有一定的缺陷,但是整体波形一致,说明实验获得初步成功。
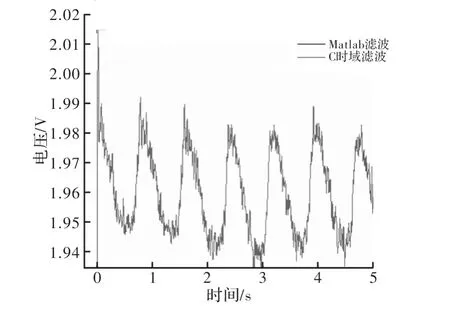
图3 C程序时域滤波与Matlab滤波比较图
7 结束语
提出了一种将硬件滤波电路数字化的方法,并在Matlab和Visual C++平台上得以实现。与模拟滤波电路和传统的数字滤波相比,不仅比传统的数字滤波算法简单快捷,而且有效防止了模拟电路中器件的寄生参数、精度、温度等的影响,使滤波更加稳定。
[1]邱关源.电路[M].北京:高等教育出版社,2006.
[2]孙肖子.模拟电子电路及技术基础[M].西安:西安电子科技大学出版社,2008.
[3]丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2008.
[4]楼顺天.基于Matlab的系统分析与设计[M].西安:西安电子科技大学出版社,1999.
[5]尚勇,刘卫东,吴顺君.IIR滤波器并行实现结构研究[J].电子学报,2000(3):46-48.
[6]王欣.离散信号的滤波[M].北京:电子工业出版社,2001.
[7]罗海.基于 FPGA的高速IIR数字滤波器设计与实现[D].成都:电子科技大学,2007.
