纯钼高温塑性变形及流变应力行为

孙晓云，胡贤磊，冯 雪，张 威

(1.安徽工程大学电气工程学院，安徽芜湖 241000)

(2.东北大学轧制技术及连轧自动化国家重点实验室，辽宁沈阳 110004)

钼及钼合金具有高温强度和高温硬度高，导热、导电性能好，热膨胀系数小等优越的机械性能和物理化学性能，被广泛用于冶金、机械、能源、化工、国防、航天航空等各个领域［1］。钼及钼合金板材作为附加值高的深加工产品更是应用于高新技术领域。然而，我国钼及钼合金板材轧制生产与钢铁及铝合金、铜合金等有色金属轧制生产相比，起步晚、轧制技术滞后，且钼及钼合金本身具有变形温度高、高温下氧化严重、抗拉强度大、温降快、抗拉强度随温度的下降而急剧升高等一系列加工特性［2］，使其轧制加工较铝、铜等有色金属困难，限制了在其应用领域的发展。采用热力学模拟实验研究金属的高温流变特性，不仅可以较准确地描述变形温度、变形程度以及变形速率等工艺参数对其流变应力的影响规律，而且可以为制定合理的产品加工工艺规程提供可靠的理论依据。然而目前人们对纯钼的热压缩流变应力行为的研究很少。为此，本文作者研究纯钼的热压缩流变行为，以期为纯钼轧制等热成形加工工艺的制定提供理论和实验依据。

1 试验条件和方法

实验所用材料为纯钼(pure molybdenum，以下简称PM)，其化学成分(%，质量分数)为0.76Fe，0.7O，0.32Si，0.2Cr，0.2N，0.08Ca。

将材料加工成φ8 mm×15 mm圆柱形热模拟试样。利用热力模拟实验机MMS-300对试样进行单道次压缩实验。设定不同的变形温度和变形速率，考察对纯钼变形规律的影响。实验方案如下:将试样以20℃/s的速率加热到变形温度，设定值为:900℃、1 000℃、1 100℃、1 200℃、1 300 ℃，保温3 min后对试样进行不同变形速率相同变形量的压缩试验(真应变 0.29)，设定变形速率为:1 s-1、0.1 s-1、0.01 s-1、0.004 s-1。为防止试样在变形过程中氧化，采用高纯氮气作为保护气体。实验时采用自制的钨钼合金锤头。

2 实验结果和分析

2.1 真应力-真应变曲线

PM在变形温度为900～1 300℃、应变速率为0.004～1 s-1热压缩变形时的真应力-真应变曲线如图1所示。由图1可见，所给变形条件范围内，PM热压缩变形时存在较明显的再结晶特征，即在一定的温度和应变速率下，当真应变超过一定值后，真应力并不随真应变的增大而增加，而是减小;在等应变速率下，真应力随温度升高而降低，在等变形温度下，真应力随应变速率的升高而升高;随着应变速率的增大和温度的降低，峰值应力对应的真应变值逐渐增大;从图1(c)可看出，在应变速率为0.01 s-1的应变速率下，当变形温度为1 200℃时，流变应力已经出现下降，表现为动态再结晶特征。

图1 相同应变速率不同温度下的应力应变曲线

2.2 热变形流变应力方程

绝大多数金属的热加工是热激活过程，描述金属热激活过程有很多经验公式，但综合评定广泛认为由Sellars和Tagart提出的包含变形激活能Q和温度T的双曲线正弦形式的修正Arrhenius公式最为准确［3］，即:

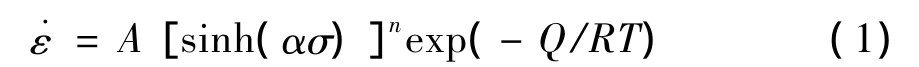
式中:A、n、α、Q均为材料常数。A为结构因子;n为应力指数;α为应力水平参数;Q为变形激活能;为应变速率;σ可表示稳定流变应力或峰值应力，或对应指定应变时的流变应力;R为气体常数，为8.314 J/(K·mol);T为绝对温度。

流变应力和应变速率在低应力水平和高应力水平下可以用不同的表达式表达［3-6］:

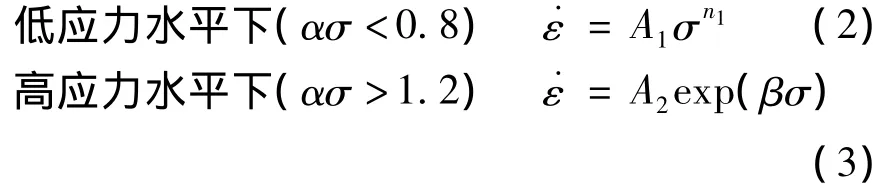
式中:A1、n1、A2和β是与变形温度无关的常数，且α和β之间满足:α=β/n1;

选取热模拟数据中变形程度为0.25(真应变)的流变应力值，以下数据计算皆采用此应力值。对式2和式3两边求对数，得:

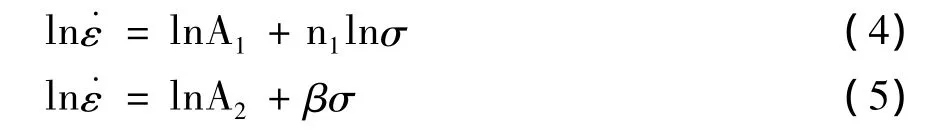
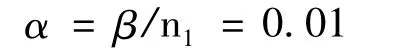
2 不同变形温度条件下lnε-lnσ曲线图

对式1两边取对数，并假定变形激活能与温度无关，可以得到:

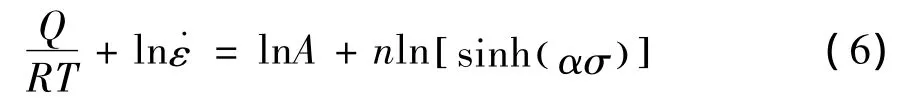
对其偏微分可得:

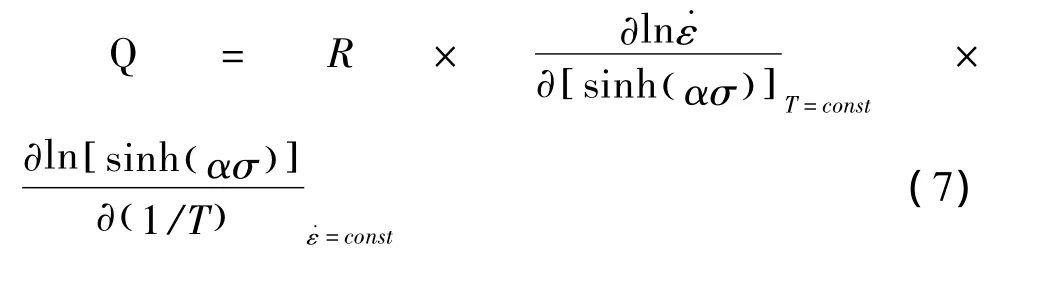
图3 不同变形温度条件下lnε-σ曲线图

令Q=R ×n×b。由式 7，以 ln［sinh(ασ)］和ln˙ε分别为横纵坐标做图4，再采用最小二乘法做线性回归，得到曲线斜率的平均值为n=4.382 41。

同理以1/T和ln［sinh(ασ)］分别为横纵坐标做图5，采用最小二乘法做线性回归，得到曲线斜率的平均值为 b=8 734.253 84。

图4 不同变形温度条件ln˙ε-ln［sinh(ασ)］曲线图

图5 不同变形温度条件下ln［sinh(ασ)］-1/T曲线图

将n值和b值代入公式7，因而求得PM的平均变形激活能 Q=318.235 6 kJ/mol。

将式1进行变形可得:

此时Z有实际特殊意义，Zener-Hollomon参数，即温度补偿变形速率因子。在再结晶研究中，他是一个表达再结晶条件的非常有用的参数。

由式9左侧可知，Z=˙εexp(Q/RT)，因Q值已求出，对于特定应变速率和变形温度所对应的Z值是可求出的。因而温度补偿变形速率因子Z值可以看做是已知参数。又Z=A［sinh(ασ)］n，对此式两边求对数得:

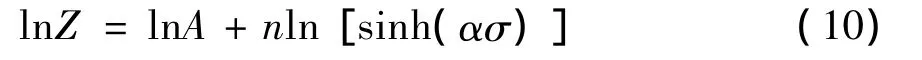
绘制 lnZ-ln［sinh(ασ)］坐标图，应用最小二乘法进行线性拟合，可得出结构因子A和应力指数n。图6为PM 的lnZ-ln［sinh(ασ)］的曲线图，由式(10)可知，该回归直线的斜率即为n值，截距为lnA 。由图得到 A=2.145 569 ×108，n=4.237 86。

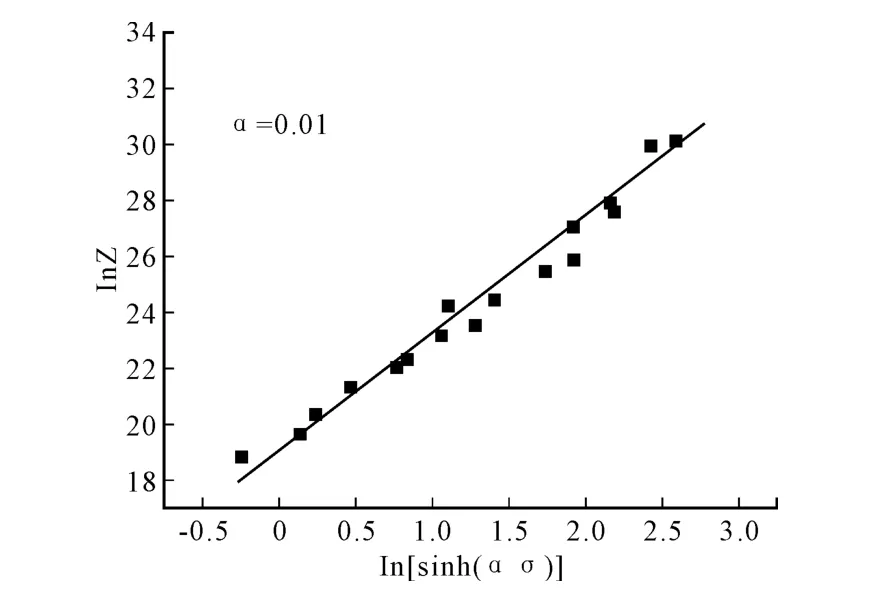
图6 ln Z-ln［sinh(ασ)］曲线图

将n=4.23带入α =β/n可得到新的α值，再带入式(7)求出第二次Q值，如此进行迭代计算，直到最后计算n值时的平均标准偏差最小。由此求得的材料常数A、n、α、Q更为真实和可靠［7］。根据以上方法最终可求得应力水平因子 α=0.032 3 MPa-1，平均变形激活能Q=318 kJ/mol，应力指数n为1.35，结构因子 A=1.59 ×107s-1。其 lnZ 与ln［sinh(ασ)］的关系如图7所示。由图7可见，两者在实验应变速率和变形温度范围内的线性关系吻合得相当好，进一步说明了PM高温塑性变形时的流变应力σ、应变速率˙ε和温度T之间的关系可用式(1)式加以描述。

将求得的A、n、α、Q等材料参数值代入(1)式，得到PM纯钼热压缩时的流变应力方程为:

图7 lnZ-ln［sinh(ασ)］曲线图

3 结论

(1)PM纯钼的流变应力曲线主要以加工硬化和高温变形软化机制为主要特征，即随着变形程度的增加，流变应力迅速升高，达到峰值后，逐步下降。流变应力随变形温度下降和应变速率升高而升高，在试验范围内出现动态再结晶。

(2)可采用Zener-Hollomon参数的双曲正弦形式来描述PM纯钼高温塑性变形时的流变应力行为，获得该合金的高温塑性变形流变应力方程为

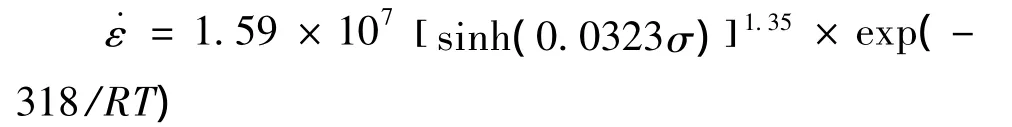
［1］付静波，赵宝华.国内外钼工业发展现状［J］.稀有金属，2007，31(6):151-153.

［2］谭 望，陈 畅，汪朴明，等.不同因素对钼及钼合金塑脆性能影响的研究［J］.材料导报，2007，21(8):80-87.

［3］Poirier J P.著，关德林译.晶体的高温塑性变形［M］.大连:大连理工大学出版社，1989.

［4］Jonas JJ，Sellars C M.Tegart W J McG［J］.Int Metall Reviews，1969，14(130):1-24.

［5］Shi H，Mclaren A J，Sellars C M，et al.Constitutive equations for high temperature flow stress of aluminum alloys［J］.Mater Sci Technol，1997，l3(3):2l0-2l6.

［6］Sellars C M，Tegart W J M.On the mechanism of hot deformation［J］.Acta Metallurgica，1996，l4(9):ll36 一l 138.

［7］Zener C.Hollomon JH［J］.J Appl Phys，1944，15(1):22.