旋转导弹电动舵机控制器超前补偿方法

王 田

(北京理工大学 宇航学院，北京100081)

0 引言

导弹的滚转方式可以克服由于发动机推力偏差、质量偏心、导弹外形加工工艺误差等干扰造成的不利影响，有效减小无控飞行段的散布。但是导弹采取旋转体制带来益处的同时，产生通道耦合，舵机控制系统延迟产生的控制误差也因此增加。闫晓勇等人基于多变量的频域设计方法研究解耦补偿方式，往往将控制耦合与运动学耦合一并分析，补偿方式类似［2］。而运动学造成的通道间耦合效应往往很小，且随转速变化不大，所以如何有效消除控制耦合即舵机相角延迟，是双通道控制解耦的重点。对于正弦控制指令跟踪下的双通道舵机系统，放宽部分时域指标，控制器中加入动态补偿环节，则可以达到频率指标提升，减小相角延迟，减弱控制耦合的目的。

本文针对舵机控制系统，建立数学模型，并进行正弦扫描辨识其模型参数，验证其正确性。结合舵机控制系统开环传递参数，为控制器设计前端校正环节。并可在实际应用中，对不同工作转速动态调整中心频率，以减小当前工作状态下的相角延迟。

1 舵机控制系统工作原理

1.1 舵机系统组成

舵机系统包括机械结构和控制电路组成。机械结构由无刷电机、传动机构、空气舵及外加负载组成如图1 所示;控制电路由控制器电路、外围信号调理电路、驱动电路等组成。

电机是机械结构中的核心部件，其工作原理动态过程可描述成如下:

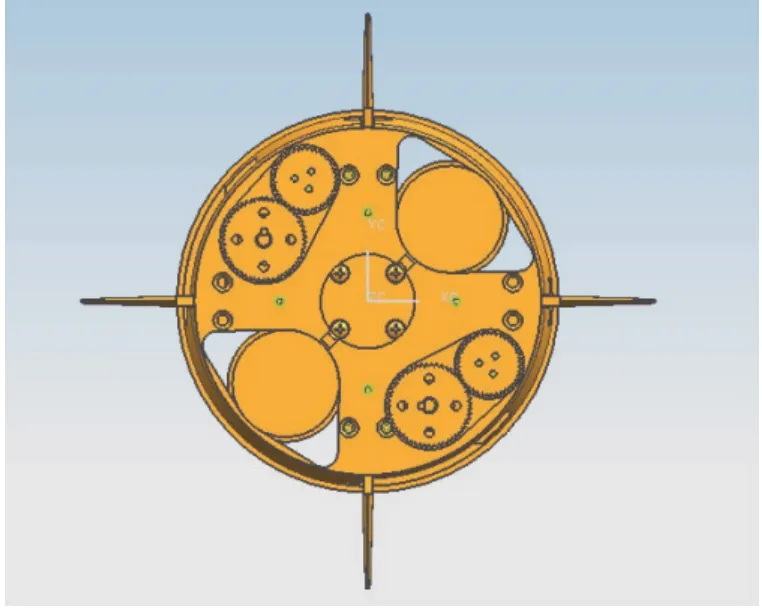
图1 舵机结构示意图Fig．1 The scheme of actuator

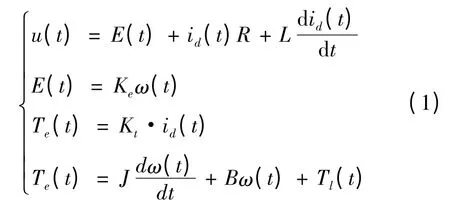
其中，Te为电磁转矩，Tl为折算到电动机轴上的负载转矩，J 为等效在电动机轴上的转动惯量，为电动机转动角速度，B 为等效在电动机轴上的粘性阻尼系数，Kt为转矩系数，Ke为反电动势系数，Kg为减速装置的减速比，u(t)为电机等效供电电压，R 为电枢平均电阻，L 为相间电感，从等效控制电压到输出舵偏角的结构框图见图2。

图2 舵机动态结构框图Fig．2 The chart of actuator system

1.2 舵机控制策略分析

旋转导弹的控制策略采用两套控制系统，正确实现对导弹俯仰运动和偏航运动的控制，而导弹滚转运动不加以控制，强制性的使其绕导弹的纵轴以一定的旋转速度旋转，靠尾翼斜置来保证固定的滚转速率。

假设控制指令信号δc使产生水平向右的偏航力，如图3 所示，则可以分解成两路舵机的δ1和δ2;在一个自转周期内，δc的指令可分解成:

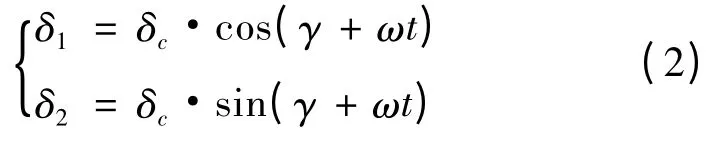
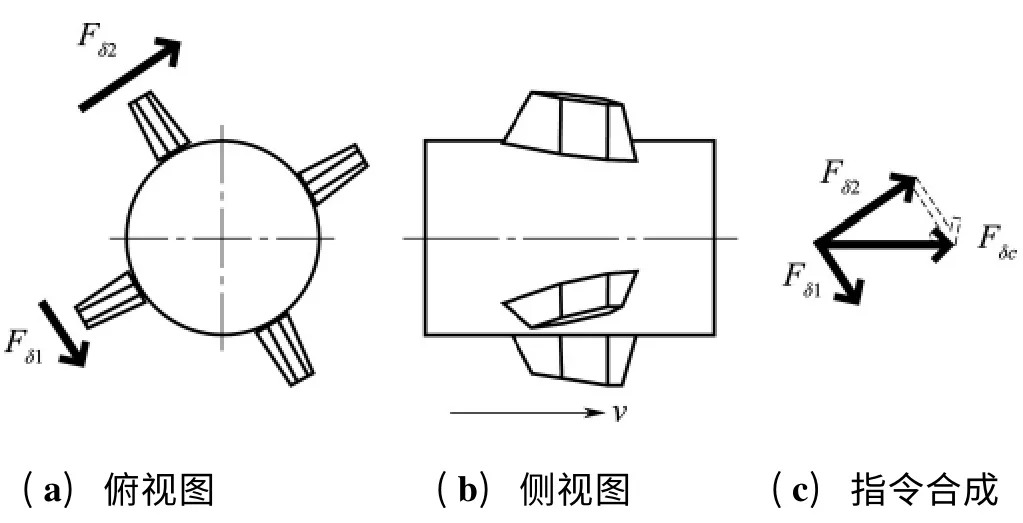
图3 旋转γ 时两通道舵机示意图Fig．3 The schematic diagram of spinning γ

电机功率、传动机构效率及结构的转动惯量、反馈回路中测量元件精度等一系列不可更改的因素，使得系统不可避免的带来了幅值大小偏差，相角时机滞后等问题，从而形成了通道间耦合。在较大转速下，当弹体旋转一定角度γ＇时，如图4所示，舵机系统跟踪指令仍是旋转角度γ 的指令值，则会产生空间上控制力与控制力矩的偏差，造成其合力绕空间转过一个γ＇- γ。

偏航方向上的作用力，由于延迟耦合到俯仰方向上。即偏航方向输入的驾驶仪指令azc会导致俯仰方向出现相应的等效ayc，这一额外的指令也会造成短周期响应的稳态偏差。

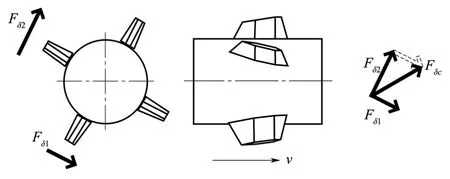
图4 旋转γ＇ 时两通道舵机舵偏角Fig．4 Theschematic diagram of spinning γ＇

舵机系统的延迟是其固有特性，在高转速的导弹中，指令周期很小，将被舵机延迟所吞没，舵机没有反应，从而影响系统的控制品质。所以旋转导弹必须研究弹体和制导系统中各部分造成的交联影响，以便采取适当的措施，进行解耦，减小交联影响。

2 导弹通道间耦合影响分析

旋转导弹由于弹体绕弹体纵轴的滚转导致了通道间的交联，产生交联的根本原因主要有:气动交联、惯性交联及控制交联。其中气动交联主要体现为马格努斯效应引起的面外力矩，惯性交联主要表现为弹体的陀螺效应，两者属于动力学耦合;控制交联主要由安装在弹体上的舵机系统的动力学延迟造成。

2.1 运动学耦合影响分析

马格努斯效应在弹体短周期运动达到稳态时仍产生影响，陀螺效应是一种输出阻尼耦合，并在滚转速度较低时对弹体稳态效果影响不大。

对滚转导弹方程进行线性化，弹体滚转造成的马格努斯效应和陀螺效应会导致弹体的输出在空间存在一定的相位偏差，该偏差可以通过弹体的动力学模型得到，基于小扰动，系数冻结假设的导弹线性化模型:

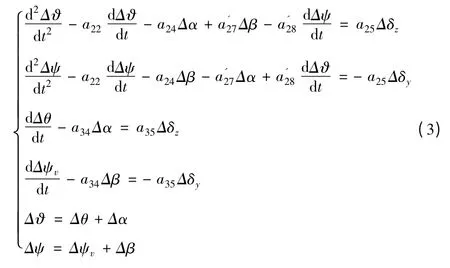
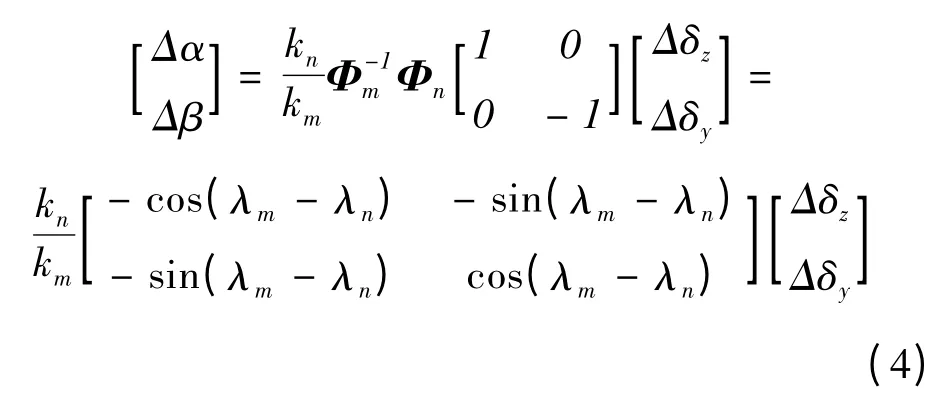
其中

λm的构成包括了由于短周期稳态马格努斯效应造成的耦合力矩、弹体主升力面提供的法向过载产生的机动对应的陀螺力矩，正负由的符号决定，一般有λm＜0 ;λn是舵面升力提供的法向过载对应的陀螺力矩产生的相位差，λn＞0 。由于舵面产生的法向过载系数a35一般远小于弹体主升力面的法向过载系数a34，运动学耦合延迟角λα= λm-λn，因此λα的符号主要取决于λm的正负。

以某型导弹在Ma = 1.5 ，α = 1° ，γ = 0°(舵面呈“X”形状)时的相关参数为例分析:

表1 模型导弹动力学参数Tab．1 Sample missile dynamics parameter

不同转速对应角度如表2 所示。

表2 各转速对应耦合角Tab．2 The couple angle for different conditions

从表中可以看到随着转速的增加，引起的耦合角度依次增加，λn本身极小，比λn高出好几个数量级，随着弹体的转速变化λm变化甚微，λm的精度变化不足以影响控制效果。需要指出的是λn、λm的确依赖于弹体的气动参数，在气动参数的获取中，辨识误差相对较大，尤其是马格努斯效应的气动参数的误差是不可避免的。

2.2 舵机系统耦合影响分析

控制耦合，指因弹体旋转使得两路舵机控制通道相互影响的现象。控制耦合包括了指令解算的延迟时间和舵机系统延迟上，旋转导弹的通道间耦合主要体现在舵机系统的时间延迟上。给舵机幅值为± 5°、频率1 ～20Hz 的渐变线性正弦指令，处理实验曲线，得到随着弹体转速变化，舵机滞后角度的关系见图所示:

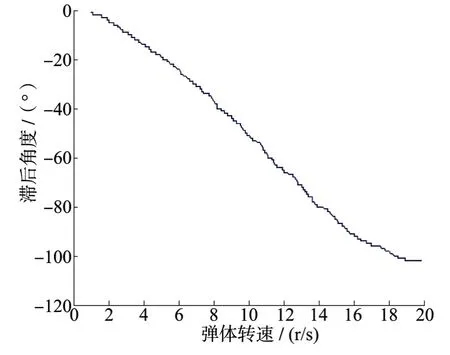
图5 舵机滞后角度Fig．5 Actuator lag angle

相对运动学耦合，控制耦合对弹体通道间耦合影响更大，即舵机系统相位延迟较大。但对于舵机的动力学系统，通过大量地面试验其系统参数辨识是能做到的。

3 舵机系统仿真分析与实验验证

对舵机系统中低频段进行参数辨识，建立精确的数学模型。基于经典控制理论，连续正弦扫频，逼近了两路舵机系统的二阶数学模型:

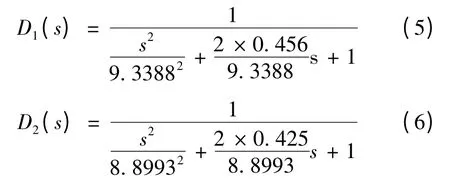
两路舵机模型差别不大，以下两路舵机均采用D1(s)模型代替，得到幅值裕度，相角裕度;基于SISO 控制系统构建校正环节，在控制器前向通路中加入串联校正装置，考虑到实际结构与控制模型之间的差距，反复推敲中心频率及开环增益降低的系数，确定中心频率ωm=79.09rad/s，α =3.24 。

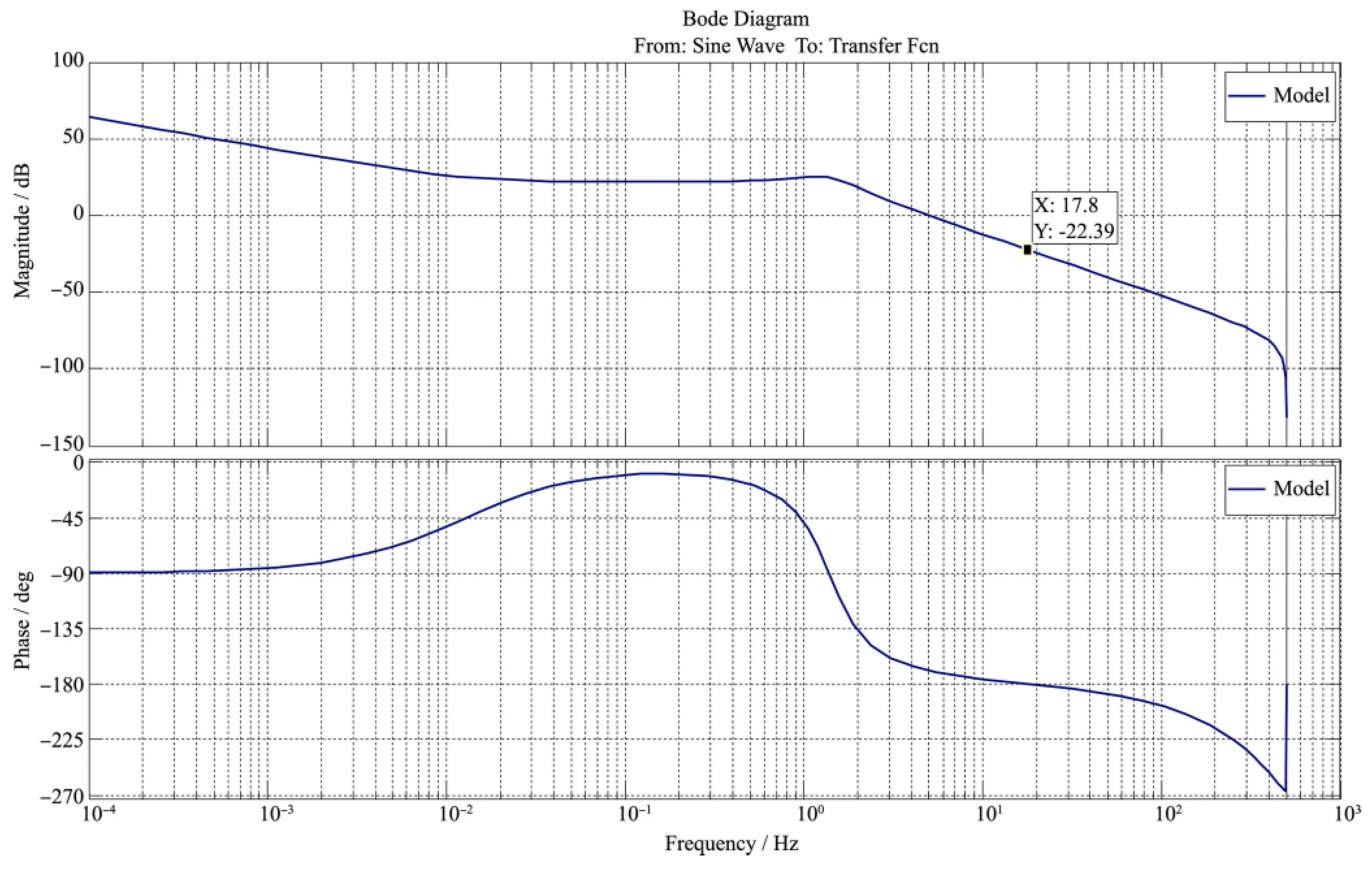
图6 舵机开环数学模型仿真Fig．6 Simulation of actuator mathematical model

更好的方法则是，围绕弹体转速f 修正fm，fm对应开环传递函数的相位超前频率点，稍大于跟踪频率即所对应闭环频率点f。则ωm= 2πfm调整，α 值在控制系统稳定的前提下取极大值。

对舵机系统进行实验测试，得到其幅相频特性如图7 所示。

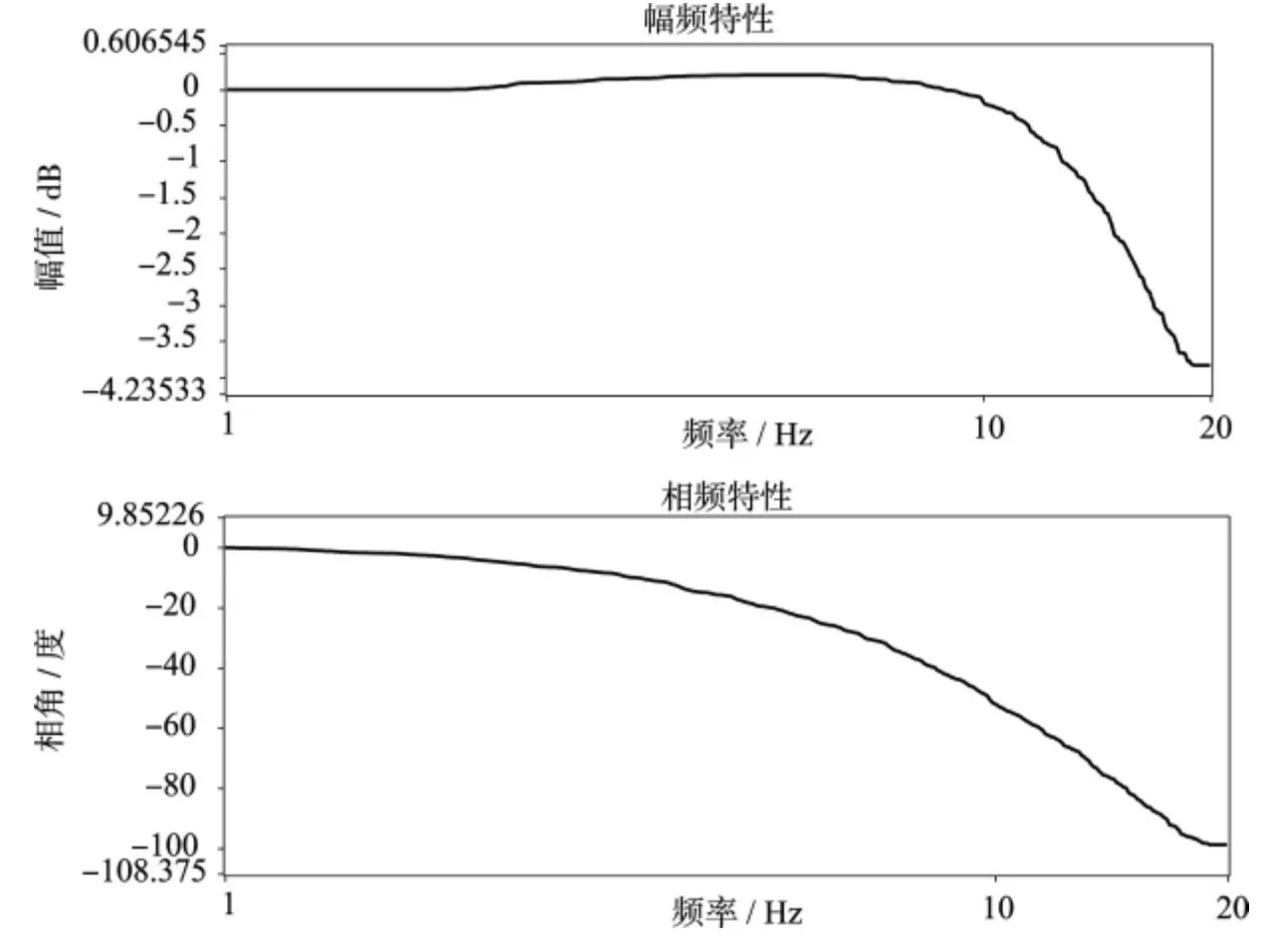
图7 实验显示舵机闭环幅相频特性曲线Fig．7 Character by the Frequency-Response Method

为解除导弹运动与制导系统产生的交联，需使控制指令提前，加入指令补偿，补偿矩阵λδ中的γc与弹体转速有关，根据速率陀螺测量值，并考虑指令延迟后获得相应补偿矩阵值。

则对于弹体回路来说在舵机指令输入端需要进行的相位补偿角度为，其中γc为舵机动力学延迟角度，τ 为指令解算时间。

指令对舵机及系统纯延迟的相位补偿矩阵为:

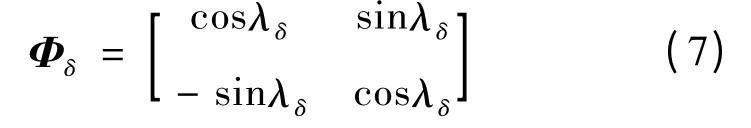
而运动学中相位补偿阵为:

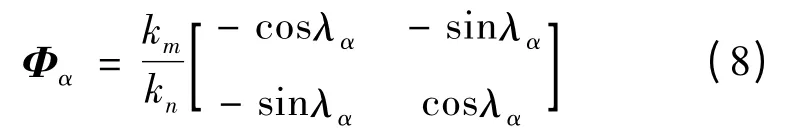
其中λα= λm- λn;

因此，动力学耦合与控制耦合，进行静态解耦补偿，则其舵机指令的补偿矩阵为:

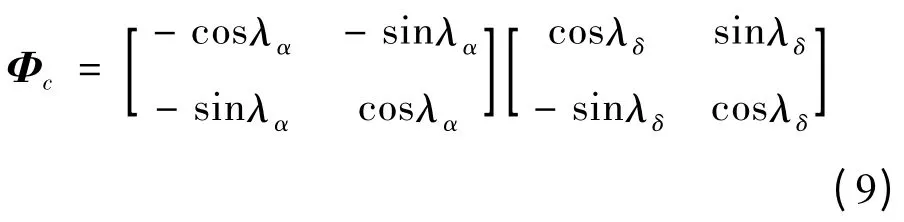
对m × m 维有理函数矩阵，令其元素为gij(s)(i，j = 1 ～m)定义对角优势度:

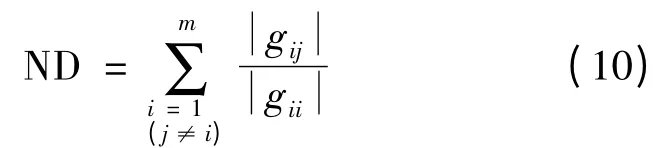
以4r/s 为例，理论上讲总可以找一个补偿矩阵，使得补偿后多变量系统完全解耦，即非对角线元素为零，ND =0，但是这种补偿矩阵可能具有十分复杂的形式，而且阶次较高，实际应用十分困难。

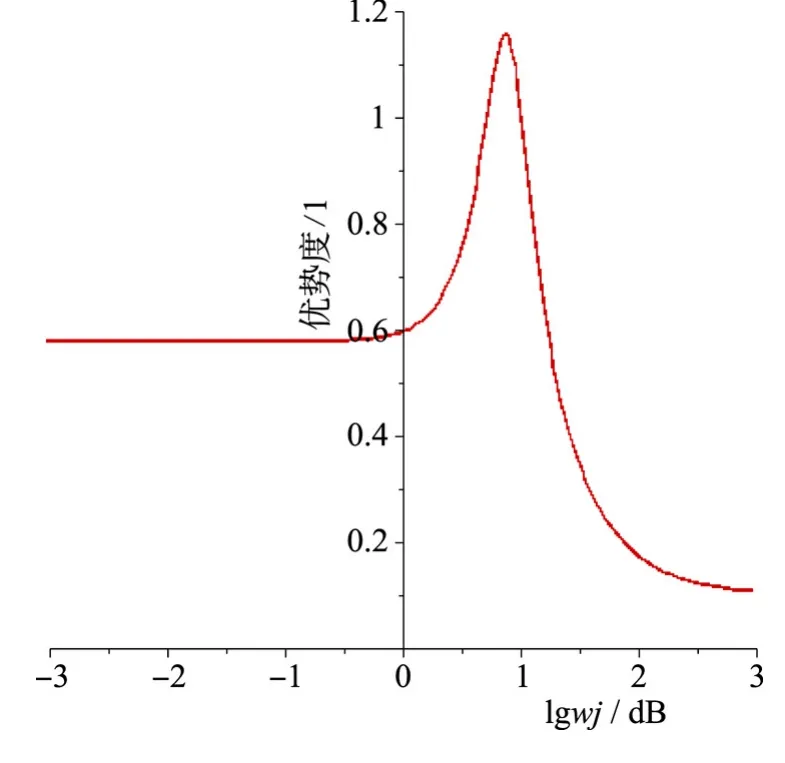
图8 转速4r/s 补偿前优势度Fig．8 Superiority in 4r/s before compensation

加入转速对应λδ的预补偿阵之后的对角优势图形:

图9 转速4r/s 补偿后对角优势度Fig．9 Superiority in 4r/s after compensation

多变量耦合系统中，设计中不需要实现系统完全解耦，只要求在工作频段内具有对角优势，为实现这一目的，非对角优势系统通常采用伪对角化方法，使得在低频工作段具有对角优势。鉴于系统模型，是基于低频段特性分析所得，所以解耦矩阵对低频段效果明显，对角元素具有较大的优势度，耦合作用减弱。使得系统工作频率不必避开固有频率，且最高耦合点向高频移动，高频段部分去耦效果不明显，但工作频段未涉及，对控制系统影响甚微。

4 结束语

工程算例中演算证明运动学造成的通道间耦合效应极小，且随转速变化不大，基本维持在-1.55° 左右，所以如何有效消除控制耦合即舵机相角延迟，是双通道控制解耦的重点。需要注意是在已知舵机控制系统相角延迟规律的情况下，才能实现解耦补偿。验证了n = 4r/s 时设计的预补偿器能满足良好的优势度，在其他转速情况下，舵机延迟时间及弹体运动学耦合不一致，需重新查询表格，设置预补偿矩阵中λα和λδ。指令预补偿矩阵的解耦方式，除了对舵机控制系统性能有足够精确的测试，还对弹体滚转角速度的反馈，马格努斯力矩系数的辨识具有较强依赖性。结合控制器前端的动态超前网络及指令预补偿，可抵消小角度下的系统延迟，对于应用双通道正弦指令跟踪的旋转导弹，具有一定的工程价值。

［1］袁天保. 弹道导弹滚动飞行动力学与控制研究［D］. 长沙:国防科学技术大学，2005. ［YUAN Tian-bao. Study on dynamics and control of Spinning Ballistic Missile ［D］. Changsha:National University of Defense Technology，2005. ］

［2］闫晓勇，张成，杨树兴. 一类滚转弹的补偿解耦方法［J］.弹道导弹，2009，21 (4):17 ～25. ［YAN Xiao- yong，ZHANG Cheng，YANG Shu-xing. Decoupling Technique for a Class of Rolling Missile ［J］. Journal of Ballistics，2009，21(4):17 ～25. ］

［3］袁天保，刘新建，秦子增. 自旋弹道导弹动力学与控制［J］. 宇航学报，2006，27 (2):217 ～221. ［YUAN Tianbao，LIU Xin- jian，QIN Zi- zeng. Dynamic and control of Spinning Ballistic Missile［J］. Journal of Astronautics，2006，27 (2):217 ～221. ］

［4］钱杏芳，林瑞雄，赵亚男. 导弹飞行力学［M］. 北京:北京理工大学出版社，2000. ［QIAN Xing- fang，LIN Rui-xiong，ZHAO Ya-nan. Dynamics of Flight for Missiles［M］.Beijing:Beijing Institute of Technology Press，2000. ］

［5］孙春香. 旋转弹双通道控制系统的理论与工程技术研究［D］. 北京:北京理工大学，2012. ［SUN Chun- xiang.Study on the Theory and Technology of Double Channel Control System of Spinning Ballistic Missile［D］. Beijing:Beijing Institute of Technology.］