四维Chen系统耦合改进的S盒的图像加密算法

李晓飞

(辽宁石化职业技术学院计算机系，辽宁锦州121001)

随着计算机信息技术的飞速发展，图像作为一类重要信息载体被广泛使用，其信息安全性越来越受到人们的关注，于是对信息安全研究的意义也变得日益重大.因此，为了确保图像信息在计算机中传播和存储的可靠性及安全性，寻求高效、安全的图像加密方法已成为研究热点［1-3］.传统的经典加密算法，如数据加密标准DES、IDEA算法以及RSA算法等，在面对大数据容量、高冗余度的彩色图像时，往往存在着许多缺陷，如密钥相对简单、密钥空间小、确定序列的参数相对较小、系统的安全性能较低等等，因此将其应用于图像加密会存在较大的弊端.

混沌系统作为一种非线性动力系统，已经在信息安全领域中越来越受到研究者的关注.其具有初值敏感性和类随机性的特点，能给加密算法提供较大的密钥空间和较强的抗攻击能力，具有更为复杂的动力学特性，因此能够很好地适应密码加密系统的要求［4-6］.如陈秋琼［7］等人利用改进的Logistic映射对彩色图像的R、G、B三层像素灰度值进行位置置乱，对置乱后的各层像素灰度值采用陈氏超混沌系统异或加密，得到彩色密文图像.该算法密钥空间大，效率安全性能好，适用于彩色图像的安全传输.朱从旭［8］等人采用一种新的自适应图像加密算法，实验结果表明，该算法存在无法进行扩散、加密前后直方图不变等情况.

目前，在对彩色图像进行加密的研究中，主要采用的是简单低维混沌系统.其存在密钥空间小、结构简单及安全性能较低等缺点，在面对大数据量的彩色图像时，无法有效地抵御穷举以及明文攻击，在实际应用中很容易利用相空间重构法将其破解.另外，在对彩色图像加密的研究中，该领域涉及的加密方法方面的研究内容相对较少，亟待深入的研究.

为了进一步研究及解决这一方面问题，在此提出一种以超混沌系统与改进的AES算法相融合的加密方法对彩色图像进行加密，并对该图像加密新算法，用其进行了仿真实验验证.

1 超混沌Chen系统和AES加密算法

该算法是利用超混沌序列结合改进后的AES加密算法对彩色图像进行加密操作.该算法在像素替代过程中采用了所设计的S盒对图像三层像素的灰度值进行替换.

1.1 4D Chen 系统

四维超混沌Chen系统.其模型如下:

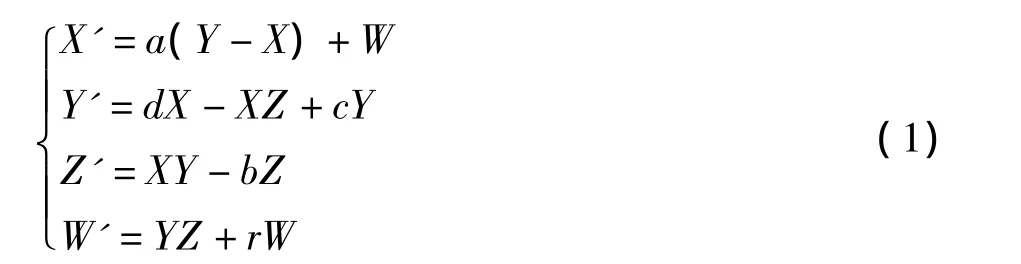
在上述公式中，X'、Y'、W'、Z'均为状态参量，是对时间 t的微分，X、Y、Z 以及 W 是系统参量，a、d、c、b 以及 r均为系统参数.a、b、c、d 的典型值分别为35、3、12以及7，r的取值范围位于［0.085，0.798］.

由上可知，陈氏超混沌系统与一般混沌系统相比，具有2个或更多的正指数Lyapunov，因而具有更为复杂的动力学行为、相空间，增加了系统的随机性和不确定性［9-11］.这表明了超混沌系统变量的多样化，具有良好的随机性、轨道难以预测与分析、复杂等特征.其生成的代码具有很强抗攻击能力以及较强的敏感性，所以适用于彩色图像的加密.

1.2 AES算法的S盒设计

通过对传统AES算法中的S盒进行设计，改进后的AES算法中S盒的生成结合了混沌序列，具有优良的正交性、复杂性及实时性等特征.S盒设计步骤如下:

1)设定 4 个变量初始值 X0、Y0、Z0、W0，利用上述陈氏超混沌系统迭代N次，得到混沌序列Xn、Yn、Zn、Wn.

2)取其中的Zn项序列，将其进行正交化(即当序列中有重复值时，系统自动将其舍去)，然后将该序列排列到1个256×256的矩阵中来完成S盒的设计.

该S盒结合了超混沌系统的复杂性、密钥敏感性等特点，当选定的初始值不同时，其产生的S盒也是变化的，加上S盒本身所具有的优良的正交性及复杂性等特点，因此将其用于对原图像像素值的替换，能够有效地抵抗各种攻击.

2 彩色图像加密算法设计

算法的置乱扩散框架如图1所示.

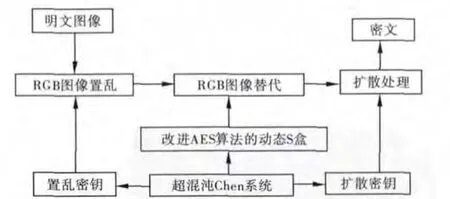
图1 加密新算法的置乱扩散结构框架

2.1 加密算法的思路

步骤1 对待加密的明文图像进行替代操作.

1)输入大小为M×N彩色图像I，分离图像获得RGB三基色分量.

2)确定参数 a、d、c、b 以及 r，设置(X0、Y0、Z0、W0)为超混沌陈氏系统变量初始值，采用四阶龙格—库塔公式对陈氏超混沌系统公式进行求解.四阶龙格—库塔公式为

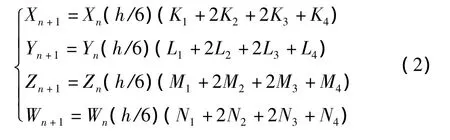
其中

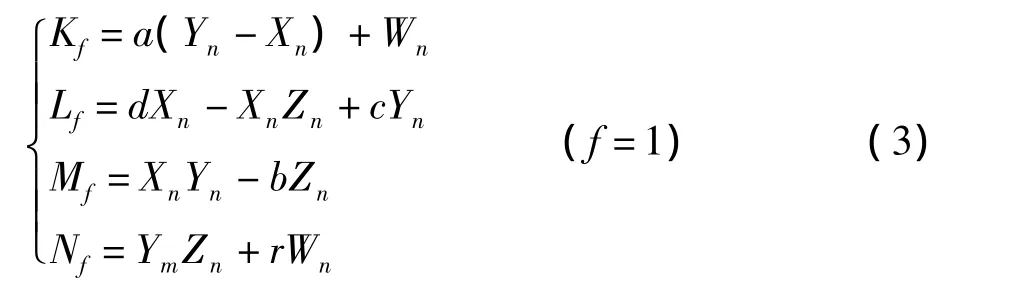
将式(2)代入式(1)中，经过N次迭代后，得到4个混沌序列 Xn、Yn、Zn、Wn，其中 h 是步长.

3)取其中的 Zn序列，将其正交化，再排列到256×256的矩阵中来获得S盒.

4)读入R层像素灰度值，用S盒来对其进行替换处理，得到替换后的R层的灰度值，其表示为R'.

5)读入彩色图像G层像素灰度值，给定不同的超混沌系统的初始值 X0'、Y0'、Z0'、W0'，按步骤 2)、3)、4)对G层灰度值进行替代，获得灰度值为G＇.

6)读入彩色图像B层像素灰度值，给定初始值X0″、Y0″、Z0″、W0″，用相同的上述方法对 B 层像素灰度值进行替代，获得灰度值为B'.

步骤2 对替代处理后得到的R'、G'、B'灰度值进行置乱操作.

1)取Xn项生成的矩阵，分别对每行的序列进行升序Xi排列及定位，得到位置序列 r(t，:)=(r1，r2，r3，r4…rn)，进行循环得到位置矩阵r.同理取Yn项生成的矩阵，对每列Yi进行升序排列及定位，得到位置序列 s(t，:)=(s1，s2，s3，s4…sn)，进行循环得到位置矩阵 s.

2)分别以r、s作为彩色图像层像素灰度值的行地址置换码和列地址置换码，最后得到置乱后的R层像素灰度值.

3)同理，按步骤1)、2)分别对 G'、B'的灰度值进行置乱处理.

步骤3 将Wn、Wn'、Wn″项序列分别排列成密钥矩阵，分别与将加密得到的 R'、G'、B'合成三基色，最后输出加密后的彩色图像.

将 Wn、W'n、W″n进行离散化处理，得到一个位于［0，255］之间的整数序列;然后离散化处理后的新序列与置乱处理后的矩阵R'、G'、B'进行二进制按位异或运算，根据明文图像的加密要求，循环执行Nr次上述操作，最终完成图像的加密.

离散化公式为

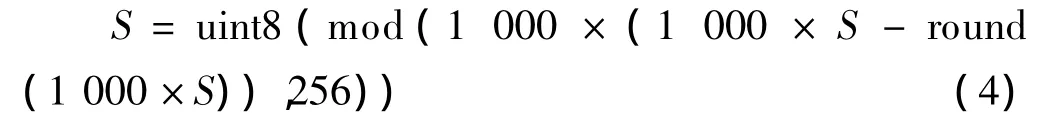
其中，S∈{Wn，Wn'，Wn″}，S 为对应的 S 序列离散化处理后的新序列.

解密操作为加密操作的逆过程，在此不做详细介绍.

3 仿真实验及结果分析

3.1 图像灰度直方图

借助仿真实验对提出彩色图像加密新算法的安全性及有效性进行验证与分析.输入1个256×256大小的标准彩色明文图像，迭代次数为1 000次，在MTLAB软件平台上进行仿真实验.同时分别给出了原始图像Lena及其R、G、B分量直方图，加密后得到密文 图 像及相应的R、G、B分量直方图.仿真结果如图2、图3所示.

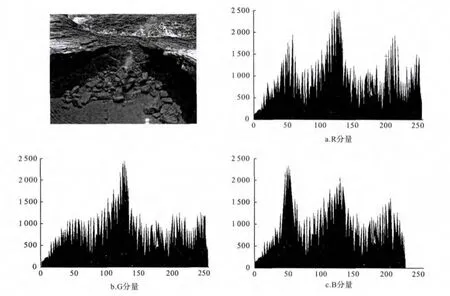
图2 原始图像及其R、G、B分量

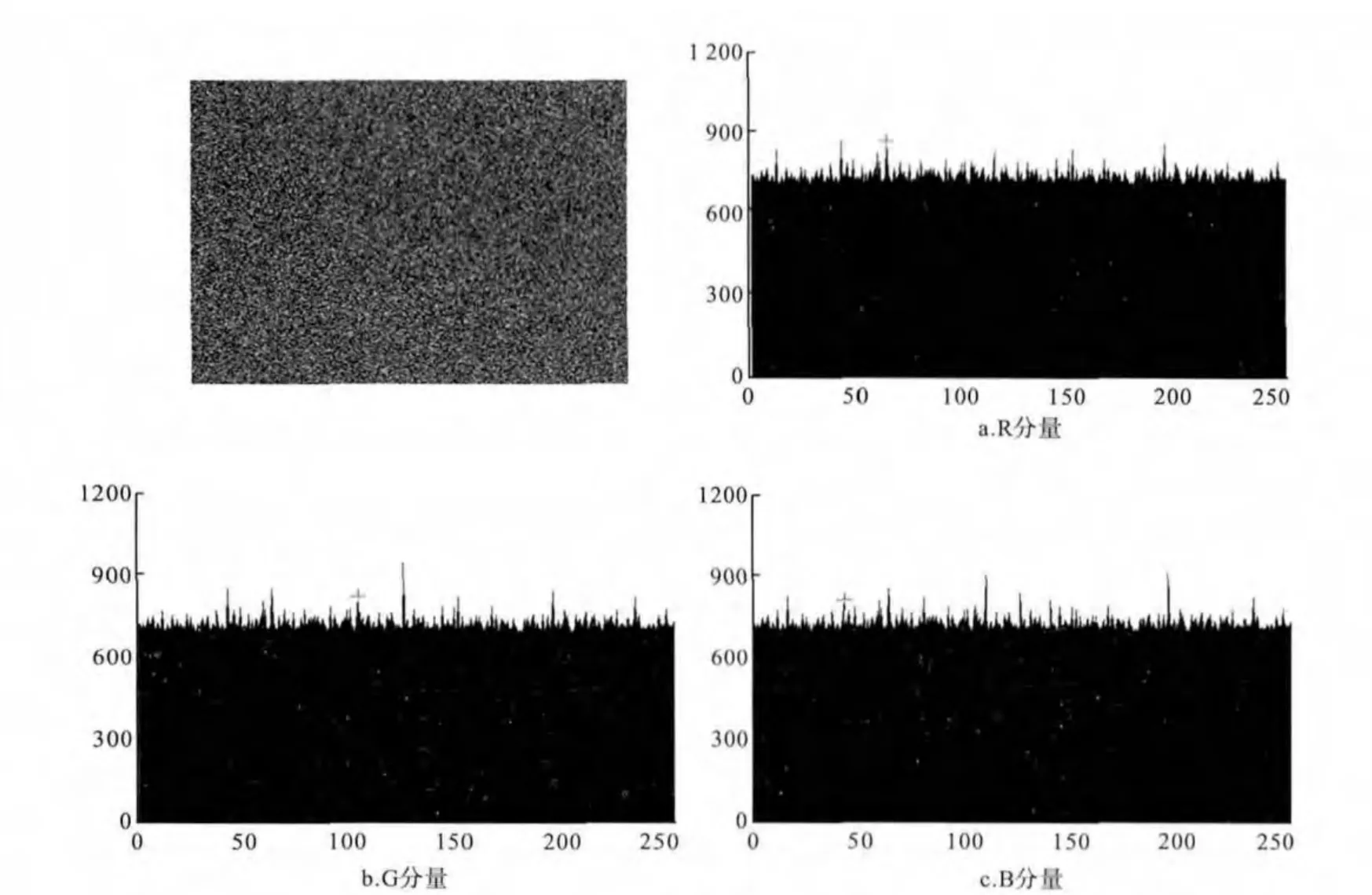
图3 密文图像及相应的R、G、B分量

从图2中可以看出，原始图像的R、G、B分量直方图波动程度较大，其随机性以及冗余性较低，很容易被攻击者获取图像相关信息.而经过新算法加密后的图像灰度直方图产生了显著地变化，如图3所示.与前面的分量直方图相比，其灰度表现出均匀状态，拥有较高的图像冗余性与伪随机性.这显示了新加密算法拥有较好的加密效果，扩散和混乱特性好，安全性高.

3.2 密钥敏感性

高效的加密系统应该具有敏锐的密钥敏感性.图4是该性能的仿真测试结果.从图中可知，只要提出的新算法中任何一个初值发生极其微小的变化(取Δ=10-5)，所产生的解密图像是完全不同的.可见，该算法具有敏锐的密钥敏感性.

图4 密钥敏感性仿真实验测试结果

3.3 密钥空间

由于较大的密钥空间能够有效地抵抗穷举攻击，因此加密系统的密钥空间越大，其安全级别也就越高.由所提出的新算法流程图1可知，该彩色图像加密算法包含置乱和扩散密钥.混沌序列产生过程中密钥空间控制参数包含了变量初始值 X0、Y0、Z0、W0、X0'、Y0'、Z0'、W0'、X0″、Y0″、Z0″、W0″以及参数 r.由于置乱密钥与扩散密钥是独立的，若新算法的计算精度为10～15，则密钥空间为(1015×1015×1015×1015×1015)3=10225.可见新算法的密钥空间是巨大的，抗攻击能力显著增强.

3.4 相邻2个像素点的相关性

一个优异的加密系统应能有效消除像素点间的相关性.在此任意择取加密前与加密后图像中的1 500对相邻像素点，采用相关系数rxy来表征该性能［12］.

图5为加密前与加密后图像的任意2个相邻像素点在X轴方向上的关联性测试结果.从图中可以看到，明文图像的R分量、G分量以及B分量的相邻像素值聚集为一条对角线，如图5a～图5c所示.这表明初始图像具有强烈的相关性，达到0.963 4;而经过提出的新图像加密算法加密后，其像素值均匀地布满了整个灰度平面，其相关性得到了有效消除，约为0.002 5.

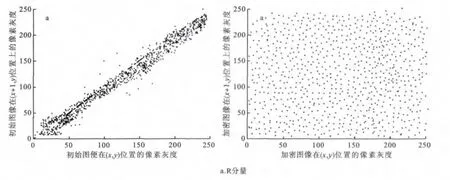
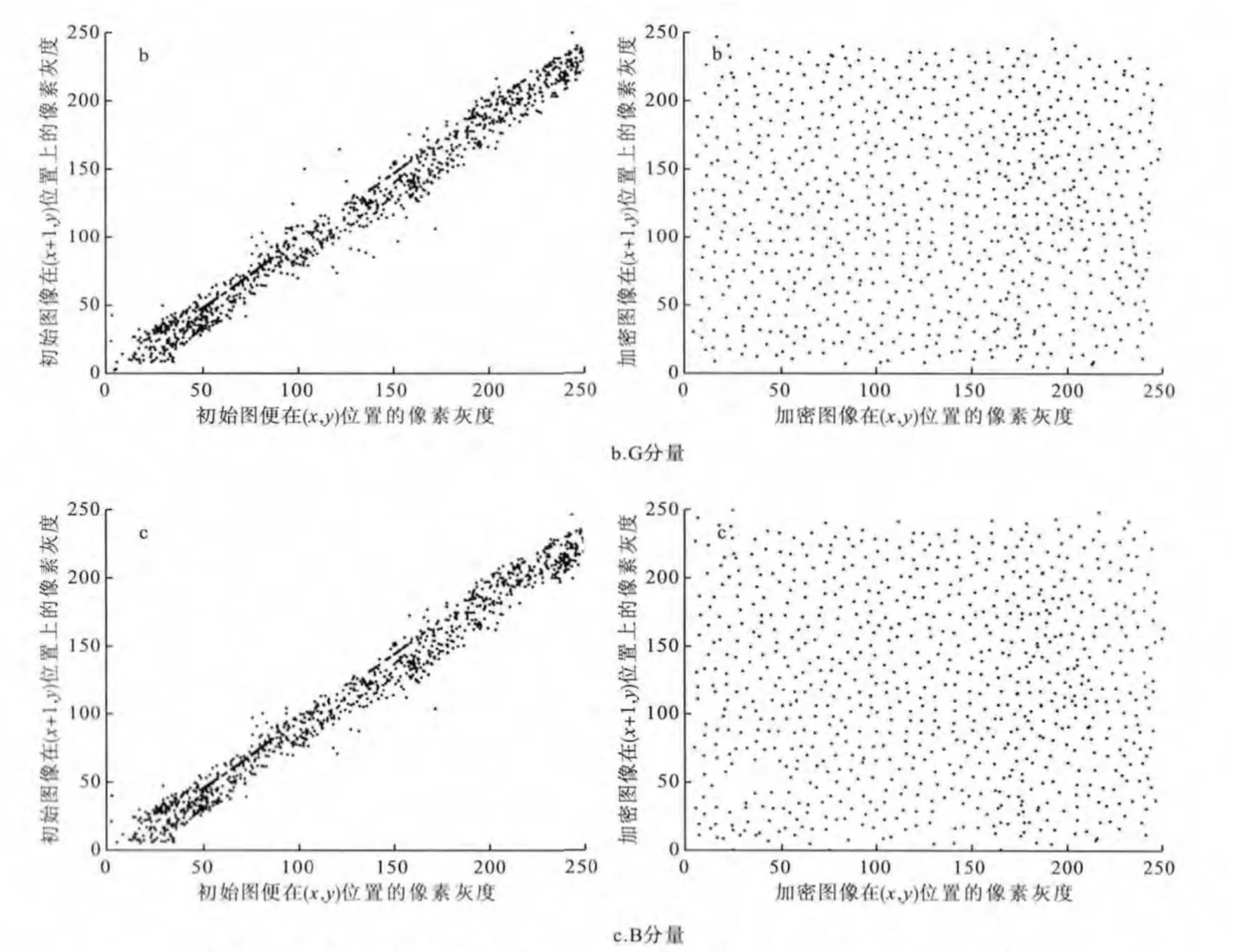
图5 X轴方向的处理前后明文与密文中相邻像素点的关联性仿真结果

表1是图像在3个方向的相关性实验结果.从表1也可以看到，明文图像具有较高的相关性，而经过提出的新加密系统之后的密文图像的相关性几乎接近零，任意2个相邻的像素点几乎是不相关的.

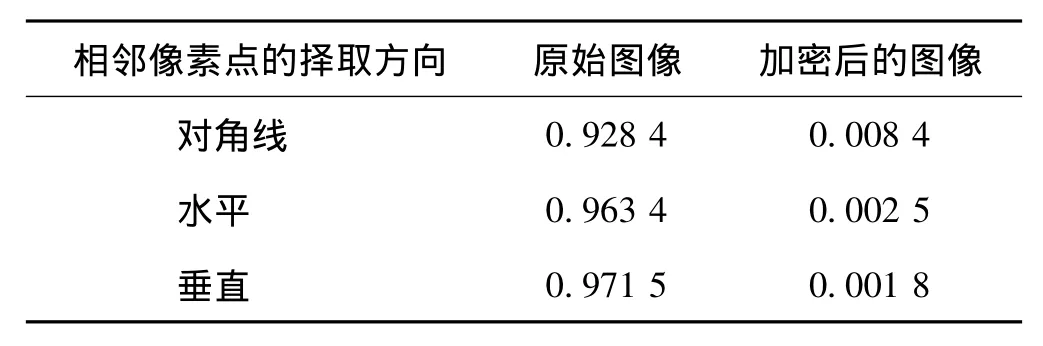
表1 加密前后的图像相邻像素点的相关度

4 结语

采用超混沌Chen系统与改进的AES算法相融合的加密方法来增强加密算法的安全性.S盒的生成结合了混沌序列，把超混沌系统的复杂动力学、密钥空间大、密钥敏感性强及抗攻击能力强等特征融入到S盒中.同时在加密过程中，将图像置乱与像素灰度值的替代结合起来，显著扩大了算法的密钥空间.通过对该算法进行仿真实验，结果表明，该算法拥有较大的密钥空间，对初值具有强烈的敏感性，加密算法高度安全.

［1］ Hu Lvping，Chen jinrong.A new chaotic map algorithm［J］.Int Bifurc Chaos，2005(12):659-661.

［2］王雅庆，周尚波.基于分数阶陈氏混沌系统的图像加密算法［J］.计算机应用，2013，33(4):1043-1046.

［3］任高峰，乔树山，黑 勇.祖冲之算法在数字图像加密中的应用与实现［J］.科学技术与工程，2013，13(3):766-770.

［4］ Atieh Bakhshandeh，Ziba Eslami.An authenticated image encryption scheme based on chaotic maps and memory cellular automata ［J］.Optics and Lasers in Engineering，2013，51(6):665-673.

［5］袁 宁.基于超混沌序列密码的保护通信技术研究［D］.长沙:国防科技大学，2007.

［6］ Yicong Zhou，Long Bao，C L Philip Chen.Image encryption using a new parametric switching chaotic system ［J］.Signal Processing，2013，93(11):3039-3052.

［7］陈秋琼，张振娟，魏 旭.基于超混沌系统的彩色图像加密新算法［J］.微电机学及计算机，2012，29(4):41-44.

［8］陈 刚，赵晓宇，李均利.一种自适应的图像加密算法［J］.软件学报，2005，16(11):1975-1982.

［9］王雅庆，周尚波.基于分数阶陈氏混沌系统的图像加密算法［J］.计算机应用，2013，33(4):1043-1046.

［10］任海鹏，庄 元.基于超混沌Chen系统和密钥流构造单向散列函数的方法［J］.通信学报，2009，20(10):102-106.