流体激振理论在风电机组叶片分析计算中的应用

李 莹，关 新，石 洋

(1.营口职业技术学院 机电系，辽宁 营口115000;2.沈阳工程学院 新能源学院，辽宁 沈阳110136;3.东北大学 机械工程与自动化学院，辽宁 沈阳110819;4.93115部队，辽宁 沈阳110031)

近些年关于风力机叶片的气动力分析的研究越来越受到业内学者的关注.吕计男等［1］根据动量叶素理论计算时域情况下风力机的响应计算，分析了叶片的几何非线性效应对响应的影响规律.张凯等［2］主要从定常流气动阻尼方面对风力机气动稳定性进行分析.孔屹刚等［3］整体分析了风轮受力大小，同时将气动载荷分析和功率分析结合计算.文献［4］从流固耦合方面进行叶片受力情况分析，并从叶片运动角度分析叶片受力变化.吴双群等［5］所编写的《风力机空气动力学》系统阐述了风力机叶片静态与常态受力和分析方法.但从瞬态角度分析叶片的研究和分析却很少，首先瞬态动力影响对风力机发电质量有一定的影响，而更重要的是对风力机叶片的运行使用寿命影响更为显著.下面将引用流体激振理论，并详细介绍此理论在风力机叶片分析中的计算方法，它对风力机叶片进行结构设计使之贴近风力机实际运行环境，提高风力机叶片的使用寿命，降低风轮维修维护成本有一定的启发作用.

1 流体激振理论概述

流体激振理论是为了确定物体在流体激振过程中的安全性，即确定物体受到激励的大小或是确定物体受流体激振的稳定性.按照流体激振基本原理，激励大致可分为强迫振动(外界流体以一定的振荡频率流动作用于物体，此作用的大小与频率取决于振荡流，与物体的阵型和固有频率无关)与自激振动(各种微小的振动会使流经振动物体的流场产生振荡，而振荡又进一步作用于振动物体，属于流场与物体之间的能量交换)2种类型.

在振动过程中，振荡流场对振动物体做正功，表明物体在振动过程中不断的从流体中吸收能量，从而使振动效果加剧.若振动流场对物体本身做负功，则流体在振动过程中起到的是阻尼作用，使系统稳定.在流场环境下的振动物体，如汽轮机的叶片颤振、风力机的叶片摆阵、气封间隙的激振等均可用激振理论进行分析计算.

总之，分析流体激振，不论是对解强迫振动和自激振动的大小，还是判断系统振动的稳定性都有重要意义，下面将在建立系统振动流场的基础上［6－7］，分析流体激振理论在风电机组叶轮机构设计中的作用.

2 叶片振荡边界条件

在求解叶片边界问题过程中，既要满足空气动力学的基本方程，也要满足边界条件.对于理想流体，叶片表面边界条件为流体在叶片表面的法向速度等于该表面的法相速度.对于真实环境下粘性流体，叶片表面边界条件为空气在叶片表面的速度等于该表面的速度［8］.

首先，叶片振荡时，叶片法向运动速度与叶面表面空气速度相等.若叶片的速度为Vy，叶片表面空气运动速度为V，则法向速度相等条件可写为

其中，n为叶片表面的法向单位向量，叶片运动的方程为

而根据梯度的关系▽F=|▽F|n，则叶片表面法向速度可表示为

设dr为x、y、z坐标方向的单位向量，则上式变为

叶片表面的空气法向速度为

将上式代入(1)式中，则有

叶片表面方程F(x，y，z，t)=0也可表示为 F(x，y，z，t)=z－F(x，y，t)=0，则(6)式中的 V·▽F 可展开为

则法向速度相等的边界条件可表示为

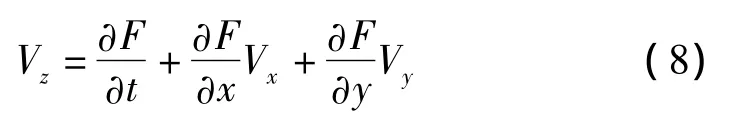
根据上式，可通过叶片两个速度分量计算第三个速度分量的大小.风力发电机组叶片在运行过程中具有2种阵型，即挥舞阵型和拍打阵型(如图1)，通过测量和计算可求出风力机叶片激振相应的大小.

图1 风力机运行过程中的阵型

3 叶片激振空气模型

在空气动力学中，空气流线上任一点的切线方向即为该点空气速度的方向，即有

根据伯努利方程，叶片翼型线是一种流线，同时沿叶片翼型线的空气参数在空气激振分析中也是至关重要的.在定常空气中，由于流动参数不随时间变化，故流线也不随时间变化.但在实际的振荡空气中，由于速度参数本身随时间变化，所以不存在一条固定不变的流线.但是在微小振荡的条件下，可将其近似处理，也就是振荡空气模型，如图2.

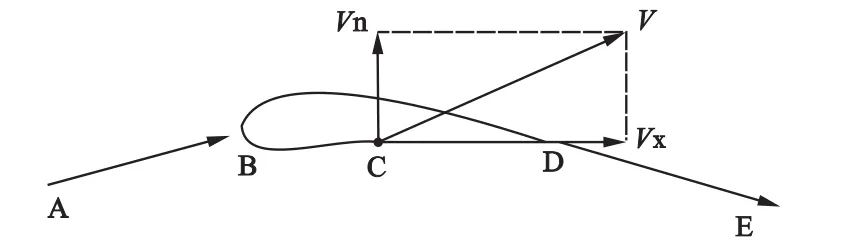
图2 激振空气流线模型

在强迫振动中，叶片翼型ABCDE曲线形状不发生变化，而是位置发生移动.在自激振动中，除了定常流速外，按照翼面切向速度的条件，还有一个法向速度可以通过叶片的自阵振频和振幅得到.因此在叶片振动时，叶片翼面上任一点E的空气速度不与叶片翼面相切，即BC不再是流线.在实际振荡过程中的速度是由定常流速度再加上由于振荡引起的垂直流线方向的振荡速度构成.在不考虑叶片几何位置变化时，单由自激角度分析，从实际角度出发，近似地可按沿着定常流线的几何位置求解.这样的物理模型可为振荡空气模型，即对于任一流动参数q，其对时间的全导数可以表示为

其中，V为振荡空气上的非定常速度，l仍为定常条件空气流线几何位置.根据此分析可近似处理风力机叶片的受力大小变化.

4 空气激振稳定性判断准则

判断叶片在振动空气流场所形成的非定常力振动情况时，若空气动力对叶片做的是正功，意味着振动过程中空气流体不断地向叶片输入能量，使物体振动加剧，即振动不稳定.若做的是负功，则意味空气对叶片振动起阻尼作用，振动随时间变化而逐渐衰减，也就是说振动是稳定的，即叶片是安全的.因此，判断叶片运动稳定与否就是判断空气对叶片做的是正功还是负功.振动横型如图3所示.

图3 叶片翼型振动模型

叶片振动1个周期的空气做功为

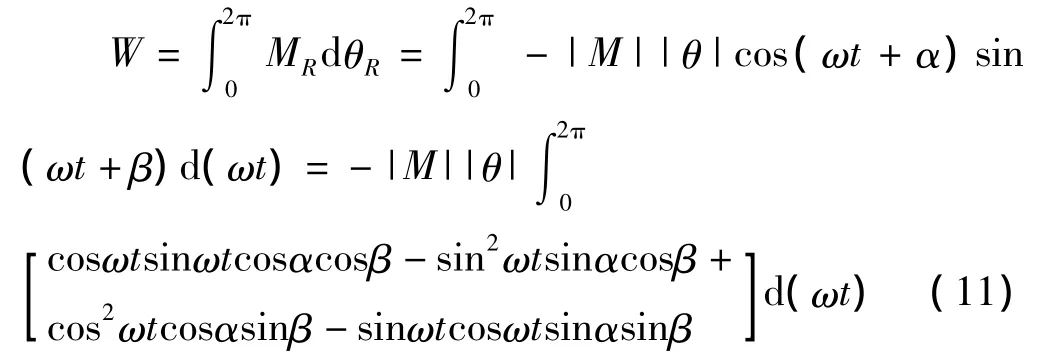
其中，θ为叶片扭转振动的位移角;β为初始相位角;M为作用在振动叶片上的空气动力力矩;α为攻角;ω为振荡频率.

若取 β =0，则 W=|M||θ|πsinα(12)，所以空气动力做功正负取决于sinα的正负，即决定于叶片运行过程中相位角的变化情况.

5 结论

1)风轮叶片振动分为自激振动和受迫振动2种.受迫振动主要为叶片宏观表现，而自激振动为叶片微观表现.

2)受迫振动主要是由于空气动力作用在叶片上的宏观表现，可分为拍打振动和挥舞振动，其主要表现为风力机叶片翼型的位置改变，即翼展方向扰度变化.针对此方面的振动问题，叶片设计时需改变叶片材质的气动弹性或增加叶片的刚度.

3)自激振动主要受叶片本身各种微小的振动与空气流场产生共鸣振荡，而振荡又进一步作用于振动叶片，属于空气流场与叶片之间的能量交换.当空气动力做功为负时，其起到阻尼作用，叶片振动趋于稳定;当空气动力做功为正时，叶片振动加剧，振动不安全.而通过计算来流空气的攻角的正弦值即可判断叶片振动是否稳定，所以为避免自激振动对风力机叶片的影响，可通过控制系统实时调节叶片攻角以达到降低叶片自激振动对叶片的影响.

［1］吕计男，刘子强，赵 玲，等.大型风力机气动弹性响应计算研究［J］.空气动力学学报，2012(2):125－129.

［2］张 凯，刘占芳，颜世军.兆瓦级立轴风力机结构动特性的气弹效应［J］.太阳能学报，2012(6):1044－1049.

［3］贺广零，李 杰.风力发电高塔系统风致随机动力响应分析［J］.振动工程学报，2011(12):696－706.

［4］关 新，孙志礼，毕孝国等.风力机运行过程中气动载荷变化工程分析［J］.工程设计学报，2012:440－444.

［5］吴双群.风力机空气动力学［M］.北京:北京大学出版社，2001.

［6］陈佐一，蒋滋康，孙锡九.振动流体力学［M］.北京:水利电力出版社，1988.

［7］陈佐一.流体激振［M］.北京:清华大学出版社，1998.

［8］章梓雄，董曾南.粘性流体力学［M］.北京:清华大学出版社，1998.