定积分在经济学中的应用

吴湘云

(丽江师范高等专科学校数学与计算机科学系,云南丽江 674100)

定积分在经济学中的应用

吴湘云

(丽江师范高等专科学校数学与计算机科学系,云南丽江 674100)

定积分是高等数学或微积分课程的核心内容，在几何学、物理学、经济学中中有广泛应用，因此成为考研数学热点和重点内容。鉴于教科书中对定积分在几何学、物理学中应用讲解较多，本文着重举例说明定积分在经济学的应用。

定积分 总成本 总收益

定积分是高等数学或微积分课程的核心内容，在几何学中有广泛应用，如平面图形的面积、体积、平面曲线的弧长[1]；在物理学中也有广泛应用，如功、水压力和引力[1]；在平均值中有重要应用，如函数平均值和均方根[1]。其实定积分在经济学中也有广泛应用，鉴于教科书中对定积分在几何学、物理学中应用讲解较多，本文着重举例说明定积分在经济学中的应用。希望对经济类大学生的学习和备考有所帮助。

1 定积分的定义及可积的充分条件

1.1 定积分的定义

设函数 f(x)在 ［a, b ］ 上有界，在 ［a, b］ 中任意插入若干个分点把区间 ［a, b］分成 n个小区间各个小区间长度依次为在每个小区间 ［xi-1,xi］ 上任取一点作函数值 f(ξi)与小区间长度 △xi的乘积 f(ξi)△ xi，并作出和记如果不论对 ［a, b］怎样分发，也不论在小区间 ［xi-1,xi］ 上点 ξi怎样取法，只要当 λ→0时，和 S总趋于确定的极限 I，这时称这个极限 I为函数 f(x)在区间［a, b］上的定积分(简称积分)，记作即其中 f(x)叫做被积函数， f(x)dx叫做被积表达式， x叫做积分变量， a叫做积分下限， b叫做积分上限， ［a, b］叫积分区间[1]。

1.2 函数 f(x)在区间 ［a, b］ 上可积的充分条件

定理1 设 f(x)在区间 ［a, b］上连续，则 f(x)在 ［a, b］上可积[1]。

定理2 设 f(x)在区间 ［a, b］上有界，且只有有限个间断点，则 f(x)在 ［a, b］上可积[1]。

2 定积分的简单经济应用

2.1 已知某经济变量的变化率求该变量

若已知某产品的总产量 Q的变化率是时间 t的连续函数，即则从时间 t=t0到时间 t=t1期间，该产品的总产量 Q的增加值为若已知 t=t0时的总产量为 Q0，则总产量函数

例1:设某产品在时刻 t总产量的变化率为 f( t) = 100+ 12 t -0 0.6t2(单 位/小时) 求从 t=2到 t=4这两小时的总产量[3]。

例2:（考研数学3试题）设某产品总产量 Q的变化率为f( t) = 200 + 5t - 0.5t2,求：(1)在 2≤t≤6这段时间中该产品总产量的增加值；(2)总产量函数[2]。

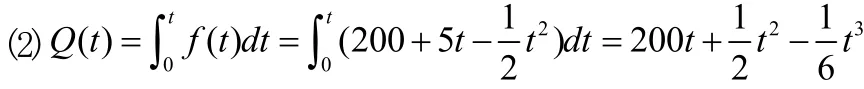
2.2 已知边际成本求总成本

若已知生产某种产品的固定成本为 C0，边际成本 M C=C′( x)，其中x是该产品的产量，则生产该产品的总成本函数是

例3设某种商品每天生产 x单位时固定成本为20元，边际成本函数为 C′( x) = 0.4 x+ 2(元 /单位) ，求总成本函数 C( x)。如果这种商品规定的销售单价为18元，且产品全部售出，求总利润函数 L( x)，每天生产多少单位时才能获得最大利润[3]。

解：固定成本为20元，即 C0=20，所以每天生产 x单位时总成本函数为

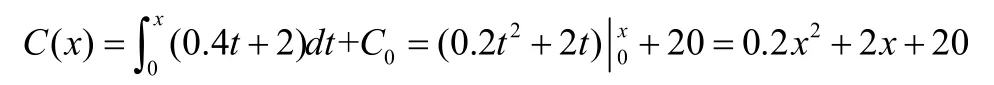
设销售 x单位商品得到的总收益为 R( x)，根据题意有 R( x)= 18x

所以L( x) = R( x ) - C( x ) = 18 x - (0.2 x2+ 2 x + 20) =- 0.2 x2+ 16 x -20

由 L′( x) =-0 .4 x+ 16 = 0得 x=40 ，而 L′(40) =-0 .4 ＜ 0，所以每天生产40单位时才能获最大利润。且最大利润为 L (40) =-0.2× 402++16× 40 -20 = 300(元 )

2.3 已知边际效益求总收益

若已知销售某种产品的边际收益 M R=R′( x)，其中 x是该商品的销售量，则销售该商品的总收益函数是

例4已知生产某商品 x单位时，边际收益函数为 R′( x) = 300-(元 /单 位) ，试求生产x单位时总收益 R( x)以及平均单位收益

例5设生产某产品的固定成本为50，产量为 x单位时的边际成本函数为 C′( x) = x2- 14 x + 111，边际收益函数为 R′( x) = 100 - 2x.求总成本函数，总收益函数和总利润函数(考研数学3试题)[2]。

3 结语

已知某经济变量的变化率求该变量，已知边际成本求总成本，以及已知边际效益求总收益等问题是定积分用于经济方面最常见的典型问题，是经济类考研数学的重点内容如(例2、例5)，应当引起重视，其实只需深刻理解定积分概念及可积充分条件，弄清题意，就可以顺利解决此类问题。

[1]同济大学数学教研室.高等数学上册(第四版)[M].北京:高等教育出版社,2001：337-342, 344-349, 351-355,357-362,364-367,277-279.

[2]刘西垣,李永乐,袁荫棠.2012年数学复习全书(考研数学三 经济类)[M].北京:国家行政学院出版社,2011:145.

[3]赵树嫄.经济应用数学基础(一)微积分(修订本)[M].北京:高等教育出版社,2003:252-253.