基于模糊C均值聚类-支持向量机的海底沉积物分类识别

尤加春, 毛慧慧 , 段文豪, 李红星

(1.中国地质大学 地球物理与信息技术学院, 北京 100083; 2.中国科学院地质与地球物理研究所, 北京100029; 3.中国科学院大学, 北京100049; 4.东华理工大学 核工程与地球物理学院, 江西 抚州344000)

海底底质类型是一种重要的海洋环境参数, 底质类型的分布对海洋科学研究、海洋工程以及国防建设等具有重要的科学与实际意义。对于海底沉积物的探测主要有直接采样法和间接采样法, 由于直接采样法的成本高, 采样效率低(只能零星采样)等缺点, 间接采样方法是目前海底沉积物类型探测的主要方法。海底沉积物的间接采样分类方法主要是利用声学、光学、地震学、生物化学等方法接受不同海底沉积物的响应, 并根据这些响应的特征进行分类。

国内外对于海底底质的分类进行了大量的研究。国外早在1947~1948年瑞典科学家Arrhenius就开展了深海勘探计划。经过数十年的发展[1-4], 国外已经形成了比较成熟的勘探技术, 海底底质分类的仪器和软件也得到了极大的发展, 例如挪威 Simrad公司的 Triton软件等。而国内对海底沉积物分类研究起步较晚。孟金生[5]、王正垠[6]利用不同的探测手段[7]研究了海底底质的响应差异并进行分类。对于实验室基础理论性的研究, 目前主要是以物理模拟为主, 例如卜英勇等[8]、邓跃红等[9]在水槽实验平台上建立沉积物模型, 利用超声回波探测不同的沉积物,并基于回波信号对沉积物进行分类研究。

实验室中的物理模拟主要是人为地按照一定比例配制海底沉积物样本, 然后再利用装置激发接受回波信号。物理模拟方法较为费时费力且实验可重复性差, 而利用计算机模拟声波探测海底沉积物并进行分类的研究鲜见于刊。本文尝试采用计算机数值正演技术模拟实际的地震勘探数据采集过程, 数值模拟方法具有快速、高效、高重复性、易于操作、经济等特点。基于不同的海底沉积物在声学上将产生不同强度的回波信号, 本文分别采用一种无监督分类方式: 模糊C均值聚类(Fuzzy C Means, FCM)和一种监督分类方式: 支持向量机(Support VectorMachine, SVM)对提取的回波的特征向量进行分类识别, 并对上述两种方法作了融合, 提出了一种新型、实用、快速高效的分类方法。此外, 数值模拟方法更有利于研究不同的分类识别方法、属性提取技术对各种海底沉积物的识别效果并为实际应用提供理论依据。

1 双相-随机介质模型

实际的海底沉积介质为典型的双相介质, 本文认为海底沉积物由岩石骨架(例如砾石、黏土等)和流体填充的孔隙构成, 利用基于双相-随机介质的弹性波动方程模拟实际地震勘探数据采集过程。基于Biot理论的双相介质弹性波动方程[10-13]为:

式中:R为流相弹性系数;Q为固流相耦合弹性系数;e为固相体应变;ε为流相体应变;u为固相位移分量;U为流相位移分量;ρ11为单位体积中固体相对流体运动时固体部分总的等效质量;ρ22为单位体积中流体相对固体运动时流体部分总的等效质量;ρ12为单位体积中流体和固体之间的质量耦合系数;A, N相当于单相各向同性弹性理论中的拉梅常数;b为耗散系数。

为能更加准确地描述实际海底复杂的沉积环境,在双相介质中引入随机扰动构成双相-随机介质, 这种随机介质[14-17]中的随机扰动可以理解为双相介质中岩石骨架弹性参数的随机变化。为了简化计算, 本文只考虑在排空情况下孔隙介质中岩石骨架弹性系数引起的非均一性, 并假设弹性系数各量的相对扰动是相同的, 从而可以只用一个相对扰动量来描述随机介质在小尺度上的非均匀性[18]。考虑空间随机介质扰动的孔隙介质弹性系数可以表示为N=N0(1+δ),A=A0(1+δ)。其中,A0,N0是背景介质的弹性参数,δ是空间随机介质通过一定的自相关函数产生的扰动。本文在研究随机介质的自相关函数时选择指数型函数来产生随机扰动:

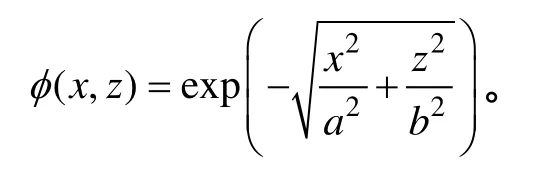
其中,a、b分别为介质在x方向和z方向上的自相关长度。

本文在已知泥岩、砂岩、砾岩的纵波、横波和密度的情况下, 将这些参数转换为泥质砾岩、泥、泥质砂岩的双相介质弹性参数, 相关等效介质理论可参考文献[19-21]。双相介质弹性波动方程的高阶交错网络有限差分离散形式参考文献[10-13, 22]。

2 分类识别方法

2.1 支持向量机

传统的统计学研究方法都是建立在大数定理这一基础上的渐进理论, 要求学习样本数目足够多。然而在实际应用中, 由于各个方面的原因, 这一前提往往难以得到保证。因此在小样本情况下, 建立在传统统计学基础上的学习方法也就很难取得理想的学习效果和泛化性能。

基于Vapnik的统计学习理论而提出的支持向量机[23-25]大大减小了算法设计的随意性, 并很好地解决了在上述问题中提到的如何在有限样本情况下实现机器学习的强泛化能力。利用支持向量机分类的基本思想是通过核函数变换的方法, 将低维空间非线性分类问题转换为高维空间线性可分的问题, 然后在新空间中求解最优分类面。

在实际的海底沉积物底质调查中, 勘测区域的沉积物样本是较少的, 研究人员需要对大量的反射波信号进行分类研究, 进而绘制勘测区域的海底沉积物底质分布情况。本文正是在这种实际需求下, 考虑有限样本情况, 利用支持向量机对海底沉积物进行分类识别研究。

2.1.1 支持向量机基本原理

支持向量机最初用来对线性可分数据进行二值分类处理的, 对线性可分问题, 给定训练样本{(x1,y1) ,(x2,y2),… ,(xN,yN)}, 期 望 输 出y∈ {-1,1},分别代表两类的类别标识。用于分类的最优超平面方程为:ωTx+b=0, 其中ω为权重向量,x为输入向量,b为偏置。支持向量机的目的是寻找一个分离边缘最大的超平面(即最优超平面)使两类数据最大可能地分离, 离最优超平面最近的特殊样本称为支持向量。则对于一确定的最优超平面, 所有的样本都满足:

对于非线性可分模式的分类问题, 会有一些样本不满足(2)式的约束条件, 而出现分类误差。因此需要适当放宽该约束条件, 将其变为:

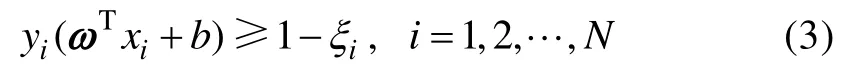
式中引入了松弛变量ξi,i= 1 ,2,L ,N, 它用于量度一个数据点对线性可分理想条件的偏离程度。当0≤ξ≤1时, 数据点落入分离区域的内部, 且在分类超平面的正确一侧; 当ξ＞1时, 数据点进入分类超平面的错误一侧; 当ξ=0时, 退化为线性可分问题。

对于非线性问题, 寻找ω和b的最优值, 使其在(3)式的约束下, 最小化关于ω和ξi的目标函数, 即

其中,Ck为惩罚系数。

利用 Lagrange乘数法求解上述最优化问题, 上述方程可变如下对偶问题:

其中,e为单位矩阵,Q为半正定矩阵,Qij=yiyjK(xi,xj),为核函数, 本文采用的 RBF核函数为, 其中2σ为给定参数。

在实际应用中,Ck和σ的选取对于支持向量机分类的效果影响极其重要, 而目前对于上述参数的选取并无统一的准则, 往往是采用大量试验的方法来获得较优的参数值, 但这种方法比较繁琐、费时,而且获得的参数也不一定能使分类效果最优。其实,选择合适的Ck和σ值使支持向量机的分类效果达到最优的问题属于优化问题。本文提出采用差分进化(Differential Evolution, DE)算法[26]实现对支持向量机参数的自动最优化搜索。

2.1.2 差分进化算法

差分进化算法[28-29]是一种随机的并行直接搜索算法, 整个算法包含3个过程: 变异、交叉、选择, 类似于遗传算法的变异、交叉和选择操作。3种操作描述如下:

(1) 变异

设有N个个体xi(t),i=1, 2, …,N, 对于第i个体xi(t), 根据下面公式生成下一代变异个体:

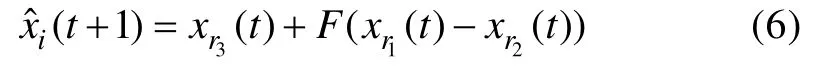
其中,xr3(t),xr2(t),xr1(t)为从进化群体中随机选取的互不相同的 3个个体, 其中i和r1、r2、r3之间必须是不同的。F为缩放比例因子, 用于控制差向量的影响大小。

(2) 交叉

为了增加群体的多样性, 交叉操作被引入差分进化算法。将个体xi(t)和变异个体进行二项分布杂交 生 成 杂 交 个 体:

具体操作如下:

其中,R∈ [ 0,1], 为杂交参数,P∈ [0,1]之间的随机数,D为解空间维数。

(3) 选择

在基本差分进化算法中, 选择操作采取贪婪策略, 即只有当产生的子代个体优于父代个体时(对应目标函数值f(xi(t+ 1 ))≤f(xi(t)))才被保留, 否则父代个体被保留至下一代。

2.1.3 基于差分进化算法的支持向量机参数优化

本文采用交叉验证(Cross Validation, CV)的思想利用差分进化算法求取支持向量机的最优化参数。CV是用来验证分类器性能的一种统计分析方法, 基本思想是在某种意义下将原始数据进行分组, 一部分用于训练集, 另一部分用于验证集。其方法是首先用训练集对分类器进行训练, 再利用验证集来测试训练得到的模型, 以得到的分类准确率作为评价分类性能指标。本文选择 K-折交叉验证(K-fold Cross Validation, K-fold CV)来评估分类模型的泛化性能。

为验证模型的测试效果, 本文以准确率作为差分进化算法的目标函数。准确率定义为: 准确率＝测试样本中分类正确的样本数/测试样本总数。利用差分进化算法对支持向量机中Ck和σ的寻优计算可转化为一个二维最优化问题。具体操作步骤为:

步骤1: 初始化参数, 给定差分进化算法的种群规模,F值, 最大迭代次数, 精度要求,R、Ck和σ的初始值。

步骤 2: 根据种群参数利用支持向量机对训练样本集进行训练, 并用训练好的模型对测试集数据进行预测, 计算每个个体的目标函数值(即准确率)。

步骤3: 根据差分进化算法中的变异、交叉由父代种群产生子代种群, 利用子代种群参数对支持向量机进行训练和测试, 计算子代种群每个个体的目标函数值; 执行差分进化算法中的选择操作。

步骤 4: 判断是否满足计算精度要求或是否达到最大迭代次数, 不满足时, 返回步骤 3; 否则, 执行步骤5。

步骤5: 迭代结束, 输出支持向量机模型最优的Ck和σ的值。

2.2 模糊C均值聚类

模糊C均值聚类[27-28]是Bezkek于1981年提出的, 它是目前广泛采用的一种聚类算法, 其主要思想是将经典划分的定义模糊化, 用隶属度来确定属于某个聚类程度的一种聚类方法。模糊 C均值聚类是模糊聚类算法中非常有效的一种, 即使对于很难明显分类的变量, 模糊 C均值聚类也能得到较为满意的效果。

考虑一个样本集合X={x1,x2,… ,xn}, 将其分为c个模糊组, 并求每组的聚类中心cj(j= 1,2,… ,C0),使目标函数达到最小。目标函数定义如下:

其中:uij∈[0,1]间;ci为模糊组i的聚类中心,C0是期望聚类的数目,为第i个聚类中心与第j个数据点间的欧几里德距离; 且m∈ [ 1 , ∞)是一个加权指数。式(8)需要满足

模糊聚类就是通过迭代最优化目标函数Jc实现的, 这是一个进行优化的过程。其中模糊隶属度uij和聚类中心cij分别为:

这个过程从一个随机的聚类中心开始, 通过搜索目标函数的最小点, 不断调整聚类中心和每一个样本的模糊隶属度, 达到确定样本类别的过程。

加权指数m控制着聚类的模糊性。m越接近于1, 聚类越趋向于突变(crisp),m越大, 结果越模糊、相对更易于反映空间的渐变性, 但过大的m值将导致类别间的重叠太多, 聚类结构不清晰, 因此对m的选取需要在模糊度与清晰度的聚类结构间进行权衡。参考文献[29]根据实验建议最佳m位于区间 [1.5,2.5]之间。

3 实验数据分析

根据前文建立的双相-随机介质模型, 利用高阶有限差分技术正演计算海底沉积物的一次反射波信号。为简化计算, 本文设计了一个双层地质模型, 第一层(0~400 m)为海水, 第二层为海底沉积介质, 该部分介质为双相-随机介质, 弹性参数的随机扰动由指数自相关函数给出, 见图1。正演模型尺度为1 000 m×750 m,空间网格步长为 5 m, 时间步长为 0.1 ms, 所用Ricker子波主频为30 Hz, 震源深度保持H= 300 m不变, 接受器置于炮点相同位置, 使之水平移动得到海底反射波的自激自收剖面, 每个模型通过正演模拟计算得到 100道地震记录。海底沉积物底质颗粒的弹性参数见表1。利用等效介质理论计算的双相介质的弹性参数见表2。根据Folk沉积物分类[30]方法, 在本文中, 泥质砾岩中砾岩: 泥岩=7∶3, 泥质砂岩中砂岩∶泥岩=1∶1。

图1 由随机函数产生的随机扰动Fig.1 Random disturbance generated by the random function

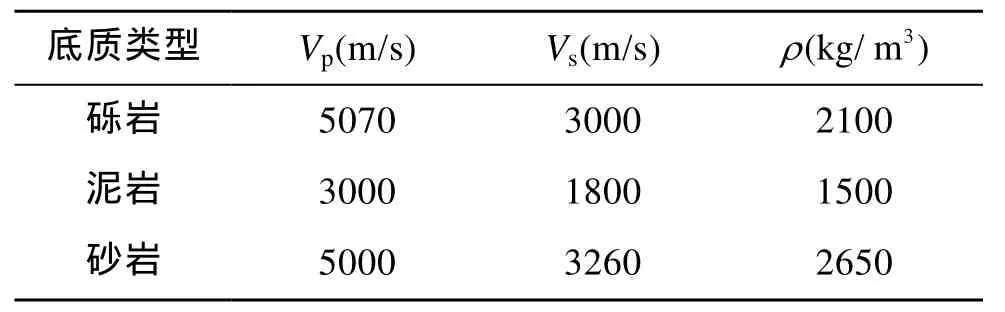
表1 固体颗粒弹性参数Tab.1 Elastic property of solid particles

在得到海底反射波之后, 利用小波变换[31]提取该反射波的特征向量。提取步骤: (1)首先对信号进行Hilbert变换得到原信号的解析表达式; (2)对信号的解析表达式的实部和虚部分别作小波变换, 之后对某一级小波分解信号求模, 即为反射波的包络特征向量。

表2 沉积物底质弹性参数Tab.2 Elastic property of marine sediments

综合考量了输入神经网络的特征向量个数应尽可能少及特征向量要充分体现反射波特性时应尽可能多的特点, 经本文试验计算后选择对小波分解的第五层系数作求模运算。 本文选择的小波基为harr小波。

有限差分正演计算的 3个模型的第 100道地震记录见图2。利用小波变换计算其包络作为特征向量见图3。本文在每个模型中选取20个一次反射波的特征向量作为支持向量机的训练数据, 将其余数据作为预测数据, 同时利用算法对支持向量机要预测的数据进行分类以便对比这两种方法的分类效果。从图4中可见利用差分进化算法优化过的支持向量机的预测分类正确率达到了100%。图5为模糊C均值聚类算法的聚类效果, 正确率也为100%。从图4、图5中可见, 支持向量机分类方法和模糊 C均值聚类分类方法均取得了极好的分类结果。

为了验证本文所用方法的稳定性, 本文对反射波信号中分别加入10%, 30%, 50%的高斯白噪音, 某一道地震记录及加噪后的波形见图6。从图中可见高斯白噪音几乎全部掩盖了原始信号的特征, 单纯地依靠人的经验已经无法区分海底沉积物底质类型了。本文仍然采用支持向量机和模糊 C均值聚类进行分类识别, 训练样本和预测样本同上。此时, 本文以训练样本的最大分类正确率为目标函数, 利用差分进化算法对支持向量机分类参数进行优化选择计算。最优化的支持向量机预测分类的结果与模糊 C均值聚类分类结果见表3。

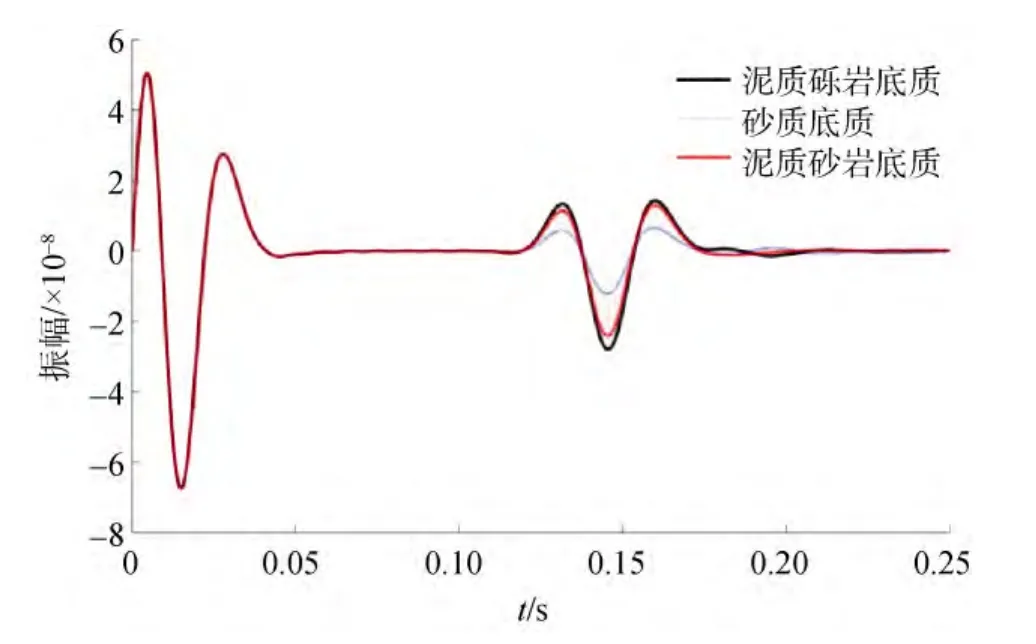
图2 三个模型第100道地震记录对比Fig.2 Seismic record of trace No.100 in three models

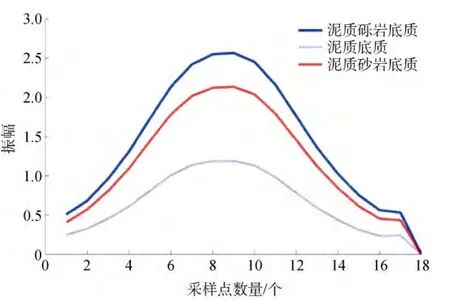
图3 三个模型反射波第100道的特征向量Fig.3 Characteristic vector of trace No.100 in three models

图4 支持向量机预测分类结果Fig.4 The classification predicted by SVM

从表3中可见, 在信号中加一定的噪音之后,模糊C均值聚类相较于最优化支持向量机预测分类的正确率明显较低。可见在低信噪比、小样本情况下, 支持向量机仍然取得了比较好的分类效果。这充分说明了支持向量机对于分类数据具有很好的泛化能力和分类识别能力且具有较好的抗噪能力和鲁棒性。

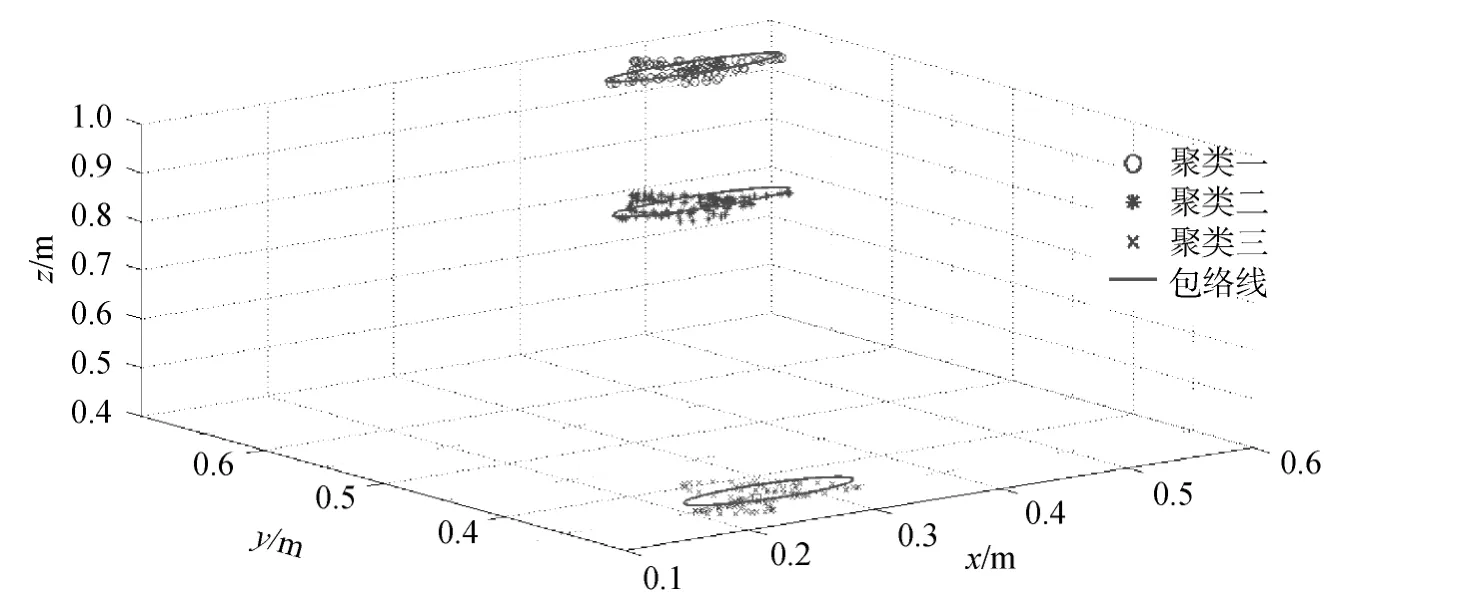
图5 模糊C均值聚类3D聚类分类图Fig.5 The clustering result produced by FCM

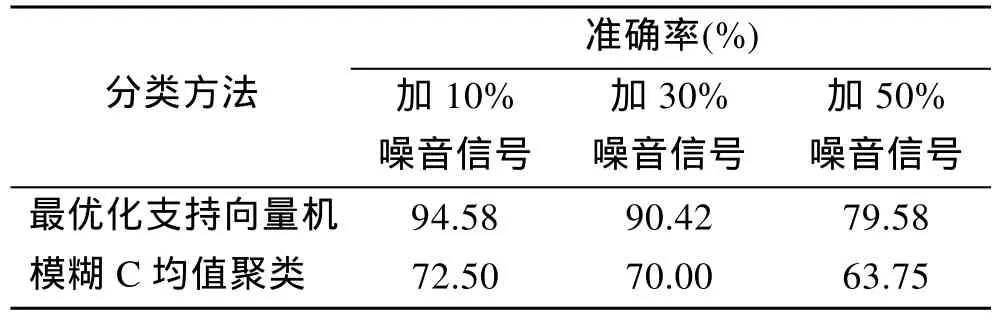
表3 加噪信号预测分类正确率Tab.3 The accuracy of using Optimized-SVM and FCM to classify the data with noise

从两种方法实现的原理上, 本文分析了模糊 C均值聚类和支持向量机对于分类识别问题各自的优缺点: 模糊 C均值聚类相较于支持向量机不需要先验信息, 直接根据聚类方法中的距离函数即可进行分类, 属于无监督分类方法, 但对噪音数据比较敏感, 分类正确率不高; 支持向量机需要一定数目的先验信息(训练样本), 属于监督分类方法, 但支持向量机对数据泛化能力强, 预测分类正确率较高。

鉴于此, 本文提出一种混合分类方法, 即模糊C均值聚类-支持向量机分类方法, 该方法充分利用上述两种方法的优点而达到无需先验信息的高精度、快速分类。这种混合分类方法, 从算法的实现上也可以称为两步分类法。两步分类法计算步骤如下:

步骤1: 数据初步聚类分析, 此步骤主要是通过模糊C均值聚类实现。具体操作如下:

(a) 确定分类数C0、m、精度要求等参数;

(b) 初始化cj(j= 1,2,… ,C0);

(c) 根据式(9)计算u和cj(j= 1,2,… ,C0);

(d) 根据式(8)计算模糊聚类目标函数, 判断是否满足聚类精度要求, 满足则算法终止, 否则返回(c)。

步骤2: 支持向量机训练样本筛选, 根据模糊聚类的结果选择最靠近每类中心的样本作为支持向量机的训练样本; 首先计算每类的类内均值, 然后计算每类的类中所有样本到中心值的距离矩阵, 从每类的距离矩阵中筛选出距离最小的若干个样本构成支持向量机的训练集;

步骤3: 在用训练数据训练支持向量机时, 利用差分进化算法对支持向量机中关键参数进行最优化搜索;

步骤 4: 用上述训练好的支持向量机模型对其余数据进行预测分类输出。

基于上述对海底沉积物数值模拟分类方法的论证, 可见本文所用方法是全完可行的。为了便于进一步对不同海底沉积物底质产生的地震反射波进行深入研究, 也为研究不同特征提取技术或其他分类识别算法对海底沉积物类型的识别能力, 本文归纳总结了利用计算机数值模拟技术对海底沉积物进行分类识别的一般化研究流程:

(1) 模型构制, 先将固体颗粒的弹性参数按照一定的体积百分比利用等效介质理论转变为海底沉积物的弹性参数;

(2) 地震反射波信号采集, 基于双相-随机介质弹性波动方程, 利用有限差分技术计算模型的地震反射波信号;

(3) 特征向量提取, 利用小波变换或其他特征提取技术提取海底沉积物底质反射波的特征向量;

(4) 分类效果评价, 利用模糊 C均值聚类-支持向量机分类方法预测分类并进行评价。

此外, 鉴于本文所提方法具备较好的函数泛化能力及模糊 C均值聚类的无监督模式识别的特点,本文所采用的方法也有利于应对实际复杂的海底沉积物底质的分类识别, 这也是本文下一步的研究目标。

图6 原始地震记录与加噪音地震记录波形对比Fig.6 The comparison of the original data and the data with noise

4 总结

海底底质类型进行分类研究一直是一个经典、热点的课题。本文在总结了前人关于海底沉积物分类研究的基础上, 率先提出采用计算机数值模拟手段来开展海底沉积物的分类识别研究。首先利用计算机数值正演技术模拟实际地震勘探数据采集过程,然后分别利用模糊 C均值聚类和基于差分进化算法优化的支持向量机对地震反射波进行分类识别, 再分析了上述两种方法的优缺点之后, 本文提出了一种对海底沉积物分类识别的两步法操作, 该方法有机地结合了模糊 C均值聚类的无监督特性和支持向量机的强泛化能力。在论证了本方法的可行性之后,本文归纳总结了一套利用计算机数值模拟技术进行海底沉积物分类识别的一般化流程以便进一步开展更加广泛深入的研究。

[1]Mackenzie K V.Reflection of sound from coastal bottoms [J].Acoust Soe Am, 1960, 32(2): 221-231.

[2]Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid, I.Low-frequency range[J].Acoust Soc Am, 1956, 28(2): 168-178.

[3]Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid, II.high-frequency range[J].Acoust Soc Am, 1956, 28(2): 168-179.

[4]Biot M A.Mechanics of deformation and acoustic propagation in porous Media [J].Journal of Applied Physics, 1964, 33(4): 1482-1498.

[5]孟金生, 关定华.海底沉积物的声学方法分类[J].声学学报, 1982, 7(6): 337-343.

[6]王正垠, 马远良.宽带声呐湖底沉积物分类研究[J].声学学报, 1996, 4: 517-524.

[7]刘建国, 李志舜.基于连续小波变换的湖底回波特征提取[J].西北工业大学学报, 2006, 1: 111-114.

[8]卜英勇, 张超, 聂双双.基于离散小波变换的水下回波信号尾波包络特征提取[J].郑州大学学报(工学版),2007, 4: 80-83.

[9]邓跃红, 聂双双.基于小波变换的水下超声波测距方法研究[J].郑州大学学报(工学版), 2007, 28(4):75-79.

[10]裴正林.双相各向异性介质弹性波传播交错网格高阶有限差分法模拟[J].石油地球物理勘探, 2006,41(2): 137-143.

[11]杨顶辉.双相各向异性介质中弹性波方程的有限元解法及波场模拟[J].地球物理学报, 2002, 45(4): 575-583.

[12]Zhu X, Mcmechan G A.Numerical simulation of seismic responses of poroelastic reservoirs using Biot theory[J].Geophysics, 1991, 56(3): 328-339.

[13]王东, 张海澜, 王秀明.部分饱和孔隙岩石中声波传播数值研究[J].地球物理学报, 2006, 49(2): 524-532.

[14]姚姚, 奚先.随机介质模型正演模拟及其地震波场分析[J].石油物探, 2002, 41(1): 31-36.

[15]奚先, 姚姚.随机介质模型的模拟与混合型随机介质[J].地球科学-中国地质大学学报, 2002, 27(1): 67-71.

[16]Li C P, Liu X W.Study on the scales of heterogeneous geologic bodies in random media[J].Applied Geophysics, 2011, 4: 363-369.

[17]殷学鑫, 刘洋.二维随机介质模型正演模拟及其波场分析[J].石油地球物理勘探, 2011, 6: 862-872

[18]李红星, 陶春辉.双相各向异性随机介质伪谱法地震波场特征分析[J].物理学报, 2009, 4: 2836-2842.

[19]Mavko G, Mukerji T, Dvorkin J.the rock physics handbook: tools for seismic analysis in porous media[M].Cambridge: Cambridge university press, 2003.

[20]Gassmann F.Uber die Elastizitat porous media[J].Vier der Natur Gesellschaft in Zurich, 1951, 96: 1-23.

[21]Gessrtsna J, Smit D C.Some aspects of elastic wave propagation in a fluid-saturated porous solids[J].Geophysics, 1990, 95: 15643-15656.

[22]Zeng Y Q, He J Q, Liu Q H.The applieation of the perfeetly matehed layer in numerical modeling of wave propagation in poroelastic media[J].Geophsics, 2001,66(4): 1258-1266.

[23]Haykin S.神经网络原理(第二版)[M].叶世伟译.北京: 机械工业出版社, 2004: 229-237.

[24]Cortes C, Vapnik V N.Support vector networks[J].Machine Learning, 1995, 20: 273-297.

[25]Vapnik V N.Statistical learning theory[M].New York:Wiley, 1998.

[26]Rainer S, Kenneth P.Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces [J].Global Optimization, 1997,11: 341-359.

[27]Bezdek J C.Pattern Recognition with Fuzzy objective Function Algorithms[M].New York: Plenum Press,1981.

[28]Bezdek J C, Hathaway R J.Recent convergence results for the fuzzy c-means clustering algorithm[J].Classifieation, 1988, 5(2): 237-247.

[29]高新波, 李洁, 谢维信.FCM算法中参数m的优选[J].模式识别与人工智能, 2000, 13(1): 7-11.

[30]Folk R L, Andrews P B, Lewis D W.Detrital sedimentary rock classification and nomenclature for use in New Zealand[J].New Zealand Journal of Geology and Geophysics, 1970, 13: 937-968.

[31]Daubechies I.小波变换十讲[M].李建平, 杨万年,译.北京: 国防工业出版社, 2004: 56-99.