基于视频数据的道路通行能力分析及车辆排队长度模型

孙文兵，杨立君

(1.邵阳学院理学与信息科学系，湖南邵阳422000;2.邵阳市第十五中学，湖南 邵阳422000)

0 引言

随着交通的发展车辆的增多，城市交通压力越来越大，尤其当发生交通意外时，堵车现象更为严重.因此正确估算车道被占用对城市道路通行能力的影响程度，将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据.

本文根据2013全国大学生数学建模竞赛A题提供的视频［1］，对道路实际通行能力进行分析并建模求解.文章先分析视频1中交通事故发生至撤离期间，事故所处横断面实际通行能力的变化过程.结合视频2分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异.构建BP神经网络模型，分析视频1中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系，并对车辆排队长度进行预测.

1 问题分析与模型假设

1.1 问题分析

由于问题给出的信息是视频材料，所以需要对视频信息进行数据的提取，这是建模的关键也是难点之一.通过观测的方法统计视频中车流量和堵车相关数据，由于观测的误差，我们每一组数据均观测三次取平均值为我们建模和分析所用的数据.

视频1记录了交通事故发生至撤离期间，事故所处横断面实际通行能力的变化过程.视频1中事故发生在第二、三车道，第一车道仍可通行.事故发生的两个车道被占用，因此这两个车道的车辆要改道才能通过，事故所处横切面的实际通行能力必由于车辆改道行为对其产生影响，于是交通事故对实际通行能力的影响可以转化为车辆变道行为对实际通行能力的影响.

对比视频2和视频1，分析说明同一横断面交通事故占用车道不同对横断面实际通行能力影响的差异.对视频2的实际通行能力的分析与视频1的方法相同.视频2中事故占用的是第一、二车道，第三车道可以通行，由于下游交通流需求不同必然导致上游各个车道分配的车辆不同，在两种不同情况下，车辆通过横断面抢道、变道通过的机率不一样，因此横断面的实际通行能力必然存在差异.这种差异可以从两方面进行分析:一、对两组实际通行能力数据的对比，从统计学理论上进行显著性差异分析;二、从两个事故不同占道情况导致这种差异的根源上进行分析.

交通事故所影响的路段车辆排队长度与事故横断面实际交通能力、事故持续时间、路段上游车流量间的复杂关系一般是非线性关系.而BP神经网络可以实现从输入到输出的任意非线性逼近.因此，考虑建立BP神经网络模型来模拟车辆排队长度与三者之间的关系，并对模型进行检验.

1.2 模型假设

(1)只考虑四轮及以上机动车、电瓶车的交通流量，假设其余车辆对交通不产生影响，换算成标准当量数，换算标准如下:

表1 不同车型的换算标准表Tab.1 The conversion standard table of different vehicle models

(2)假设车辆到达事故所处横切面之前的变道行为不影响实际通行能力.

(3)查阅相关资料假设标准车身的长度为6米.

2 道路实际通行能力影响因素分析

2.1 交通实际通行能力与车辆变道行为的关系

分析视频1，由于事故发生占用了两个车道，只有一个车道可供车辆通行，当车辆不多时，交通环境较好，道路通畅，驾驶员不需要过多的变道行为.当车辆增多，前方道路阻塞，驾驶员为了满足驾驶要求不得不变道行驶，由于过多的变道行为必然影响实际通行能力.

道路通行能力是指在给定的道路和交通条件下，道路上的某个断面或某个规则的路段上单位时间内平均最大能够通过的车辆数，实际通行能力随道路和交通条件而改变［2］.因此，在车流量高峰时段可以用单位时间内实际通过事故所处横断面的的车辆数近似代替实际通行能力(pcu/min).

通过对视频的观测，只讨论事故发生后视频的前13分钟车流情况(后4分钟视频存在少许缺失).首先统计出各种类型的车辆的车流量的数据，每一分钟统计一次数据，并将各种类型的车辆通行情况转化为标准车辆，得出标准车流量，并统计出这段时间内变道通过事故处横切面的车辆数，进而求出车辆变道行为的发生率(即变道车辆数与通过横切面的车辆数之比)，见表2.然后作出车辆实际通行能力与车辆变道行为发生率的关系图(图1)，由于事故持续的第3分钟和第8分钟并非是车流高峰期，此时的车流量不能近似代替实际通行能力，这两个数据在不具典型性，因此建模和分析中将这两个数据剔除掉.

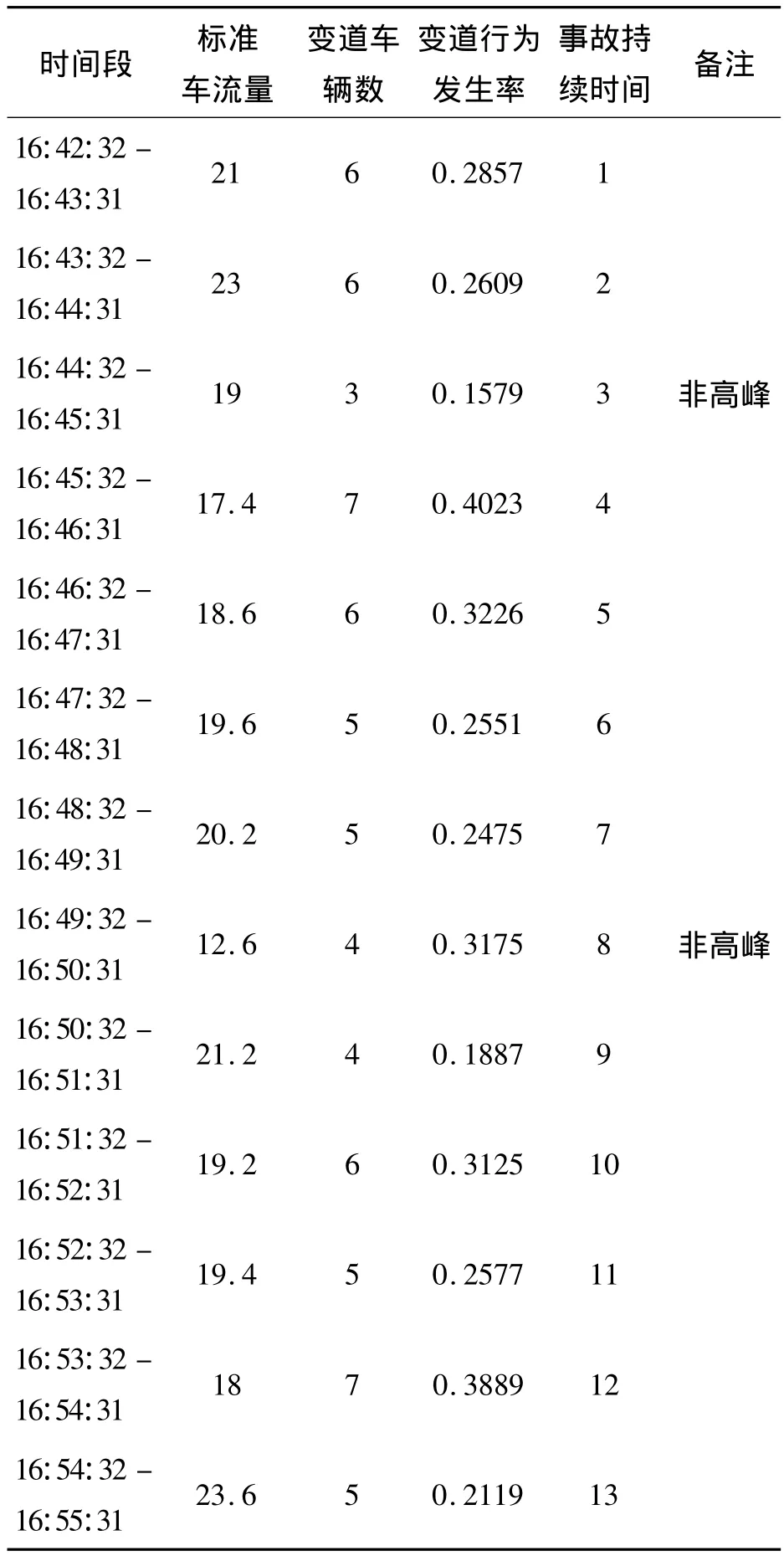
表2 视频1事故所处横切面车流量与变道情况统计表Tab.2 The statistics table between traffic flow and lanes changing in transection of traffic accident in video 1

图1 车辆实际通行能力与车辆变道行为发生率的关系图Fig.1 The relationship figure between the rate of lane changing and traffic capacity

由图1可以看出事故所处横切面处的实际通行能力总体趋势:随着车量变道行为发生率的增加，实际通行能力逐步降低.当然由于是用观测到的实际车流量代替实际通行能力，所以个别数据有一定误差，但并不影响结论的整体趋势.

2.2 交通实际通行能力随时间变化趋势

根据表2中观测到的车流量，做出事故发生过程中实际通行能力(车辆高峰期的实际车流量C)随时间(t)变化趋势图(见图2)，并用如下多项式函数对实际通行能力进行拟合.

由于真正影响预报场的是误差增长最快方向上的小扰动,因此本文首先分析飑线模拟过程中的误差分布特征,找寻预报不稳定区域所在,为BGM的改进奠定基础。文中数值模拟误差是指控制预报场与分析场资料之差。

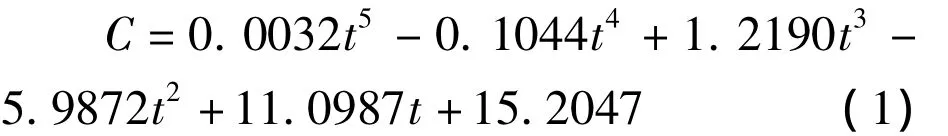
图2描述了交通事故发生过程中实际通行能力随时间变化的趋势:事故从16:42:32开始，由于刚发生事故交通暂时未造成拥堵，车辆能有序通行，此时实际通行能力较大，随着车辆的增多，道路开始拥堵，到第4分钟(即16:46:32)道路拥堵严重，此时较多车辆抢道通行，导致实际通行能力降到最低(17.4pcu/min).此后通行能力持续上升，应该与交通指挥人员对现场疏通作用有很大关系(16:46:40时，一辆交通疏通车辆达到现场，此时有人下车指挥交通到16:49:40离开现场)，到第9分钟(即16:51:32)道路畅通通行能力达到最大.然后道路又开始拥堵(应该与交通指挥人员离开有关)，到第12分钟又降到较低值(18pcu/min)，此时变道抢道通行的车辆达到7辆之多.到第13分钟，通行车辆迅速增多，因为上游车流量增加，但车辆排队秩序井然.

图2 事故发生过程中实际通行能力(C)随时间(t)变化趋势图Fig.2 The tendency chart of actual traffic capacity with time in the accident

2.3 交通事故占用车道不同对横断面实际通行能力影响的差异

为了研究交通事故占用车道不同是否对实际通行能力产生不同的影响，需要对两个视频中的实际通行能力数据进行显著性差异的分析.对视频2，在车辆高峰时段通过事故所处横切面的实际车流量(pcu/min)以及变道车辆数进行抽样观测，选取19个样本点，统计结果见表3.对视频1，选取表2中除开非高峰时段的两个样本以外的其余11个样本进行分析.

两组独立样本总体分布不了解的情况下，通过对两组独立样本的分析推断来自两个总体的分布是否存在显著性差异，可采用两独立样本的非参数检验.这里采用曼-惠特尼U检验，提出原假设:两组独立样本来自的两总体的分布无显著性差异.

检验过程利用 SPSS19.0软件［3］完成，检验前按照规定的格式组织好数据，设置两个变量，一个存放样本值，一个存放组标记值，检验结果见表4和表5.

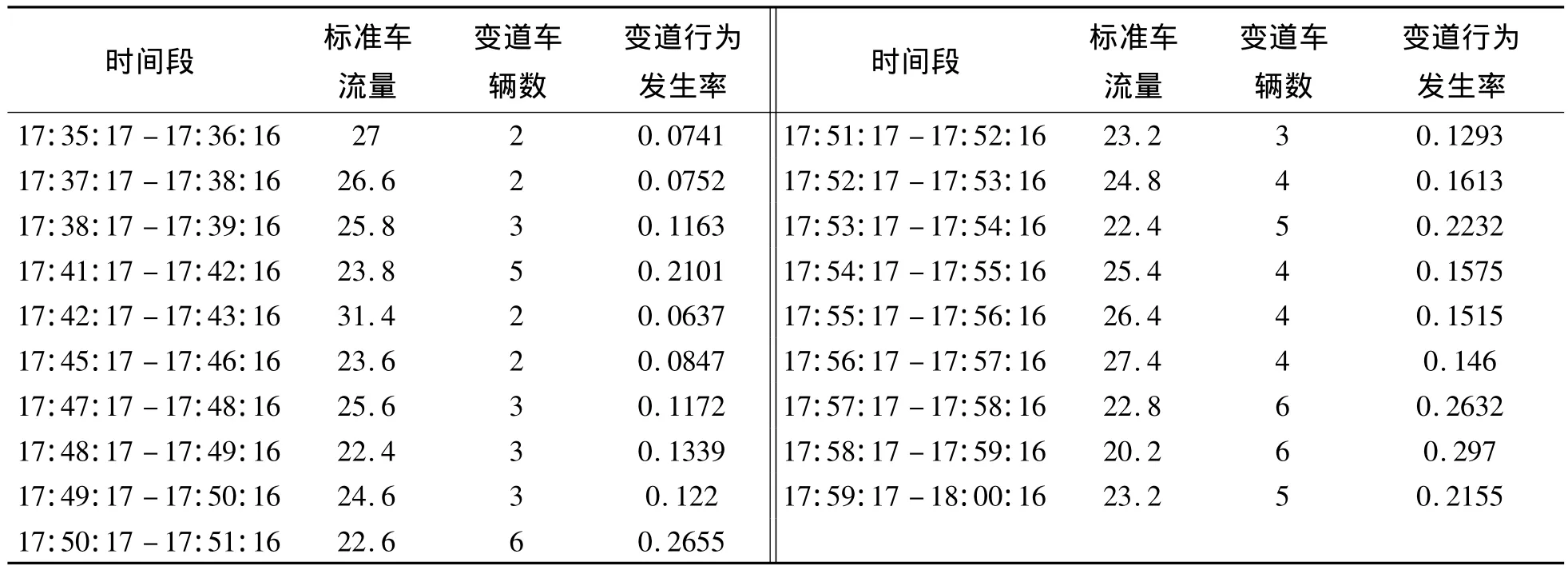
表3 视频2车道流量与变道情况统计表Tab.3 The statistics table between traffic flow and lanes changing in video 2

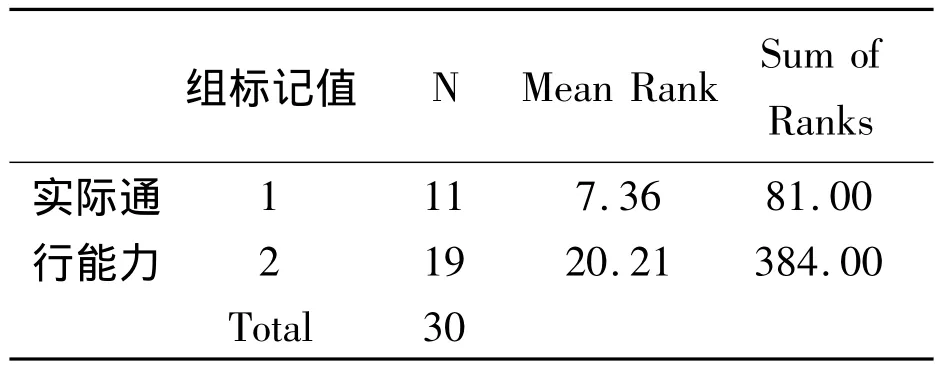
表4 两个视频中实际通行能力的曼-惠特尼U检验结果(一)Tab.4 The Mann Whitney U test results(Ⅰ)of actual traffic capacity in two videos

由表4可知，从视频1和视频2中分别抽取了11个和19个样本，两组的秩和分别为81和384.

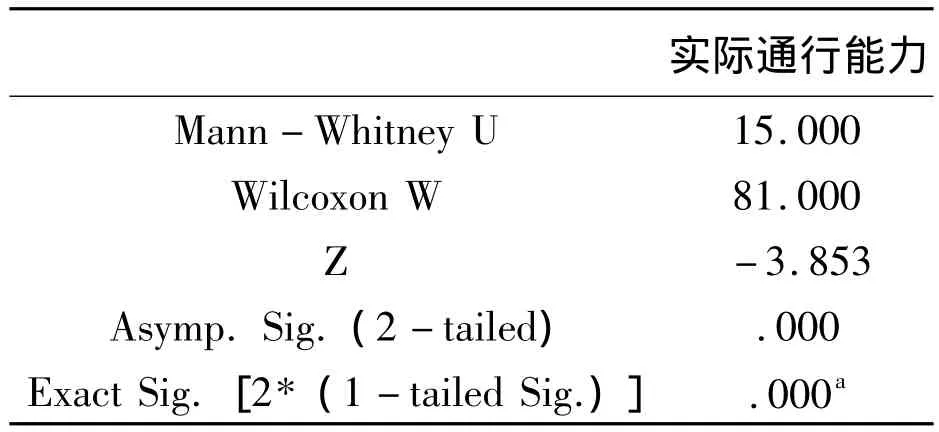
表5 两个视频中实际通行能力的曼-惠特尼U检验结果(二)Tab.5 The Mann Whitney U test results(Ⅱ)of actual traffic capacity in two videos

由表5可知，Wilcoxon W统计量取视频1实际通行能力的秩的总和81，U，Z统计量分别为15和-3.853.由于是小样本，因此采用U检验，相应概率为精确概率.如果显著性水平α=0.05，由于精确概率P-值为0.00，小于显著性水平α，因此拒绝原假设，即认为两个视频中车道实际通行能力的分布存在显著性差异.

2.4 实际通行能力与车辆变道行为的关系对比

两个视频中事故发生占用的车道不一样，通过对实际通行能力数据的统计学检验，发现两者存在显著性差异.路况条件相同的情况下，车辆变道行为实际是对车辆实际通行能力的一种干扰.通过数据统计，两个视频中单位时间(min)车辆平均实际通行能力与平均变道行为发生率的关系见表6.

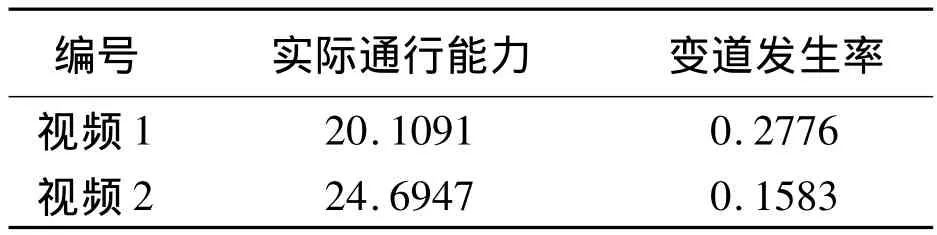
表6 实际通行能力(pcu/min)与变道行为发生率的关系对比Tab.6 The contrast of relationship between actual traffic capacity and the ratio of lane changing

3 车辆排队长度预测模型

3.1 基于二流理论的排队长度的计算及数据提取

假定交通流在单车道运行，遇到交通事故排队时，实际交通流分三个部分［4］:第1部分车流速度为0，车辆停滞;第2部分车流速度逐渐增大，交通流密度逐渐减少;第3部分车辆正常行驶，交通流不受排队的影响.第1、3部分是一种均匀流，第2部分是一种从3到1的过渡状态，不同程度地受车辆排队的影响.为了处理好第2部分交通流以便更好的反映车辆排队现象，Herman等［5-6］提出了城市交通二流理论，该理论将交通流中的车辆分为运动车辆和停止车辆两类.根据二流理论，将第2部分过渡交通流看成是第1部分阻塞交通流和第3部分行驶交通流的某种加权和，故只考虑两种均匀交通流.

基于二流理论的思想，统计车辆排队长度时，将第2部分交通流速度较慢较拥挤的一部分看成第1部分的排队车辆(在统计数据时不可避免的带有一定主观性).

设Ni为t=i时刻时排队的车辆数，C'i为t=i时刻路段上游的车流量(包括两个小区路口流入的车流量)，由于事故发生时，上游路口正好是绿灯，此时车道内的车流量较大，Q为事故刚发生t=0时，行驶在事故横断面距离上游路口的三条车道内的车辆总数，通过观测Q=19.4，Ci为事故所处横断面的实际通行能力，所以事故发生时，排队的车辆数:

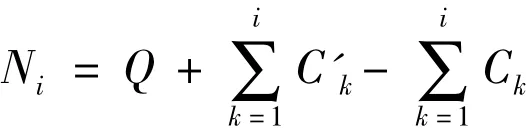
假设车身的长度平均为L=6米，根据视频中5个120米的标识以及对120米内的车辆数的观测，排队时交通流跟车距离平均约为l=2.5米.交通拥挤状况下，车辆会占据三车道进行排队，车流量和排队车辆数都化为标准车当量数，车道数m=3.

所以排队长度Li计算公式:

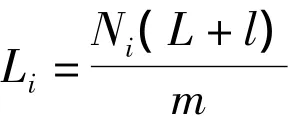
由于视频1少数部分数据缺失，所以采用抽样的方式选取具有代表性的前13分钟的车流情况的数据作为我们建模的依据，通过观测的方法每一分钟提取一次数据，由于第3分钟和第8分钟的数据是车流量处于非高峰期测得，所以实际通行能力样本不采用这两个数据，得到堵车发生时排队长度情况表，见表7.

3.2 BP神经网络模型的建立

车辆排队的长度受各种因素的影响，交通流模型往往是无穷维的、随机的、时变的、非线性的和高阶的非常复杂的动力学系统［7］，一般难以准确的找到车辆排队长度与其他三个参数之间的动力学模型，而且这些模型一般误差较大［8-9］.而BP神经网络是一种多层前馈神经网络，可以实现从输入到输出的任意非线性逼近，具有良好的自组织、自适应和容错性，应用十分广泛［10-11］.为了分析视频1中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系，考虑建立BP神经网络模型.排队长度为输出变量，事故横断面实际通行能力、事故持续时间、路段上游车流量作为输入变量.由表7，除开第3分钟和第8分钟以外取其余11个样本进行建模，前8个号样品作为训练数据，输入网络模型学习训练，后3个号样本作为检验数据以检验模型的泛化能力.

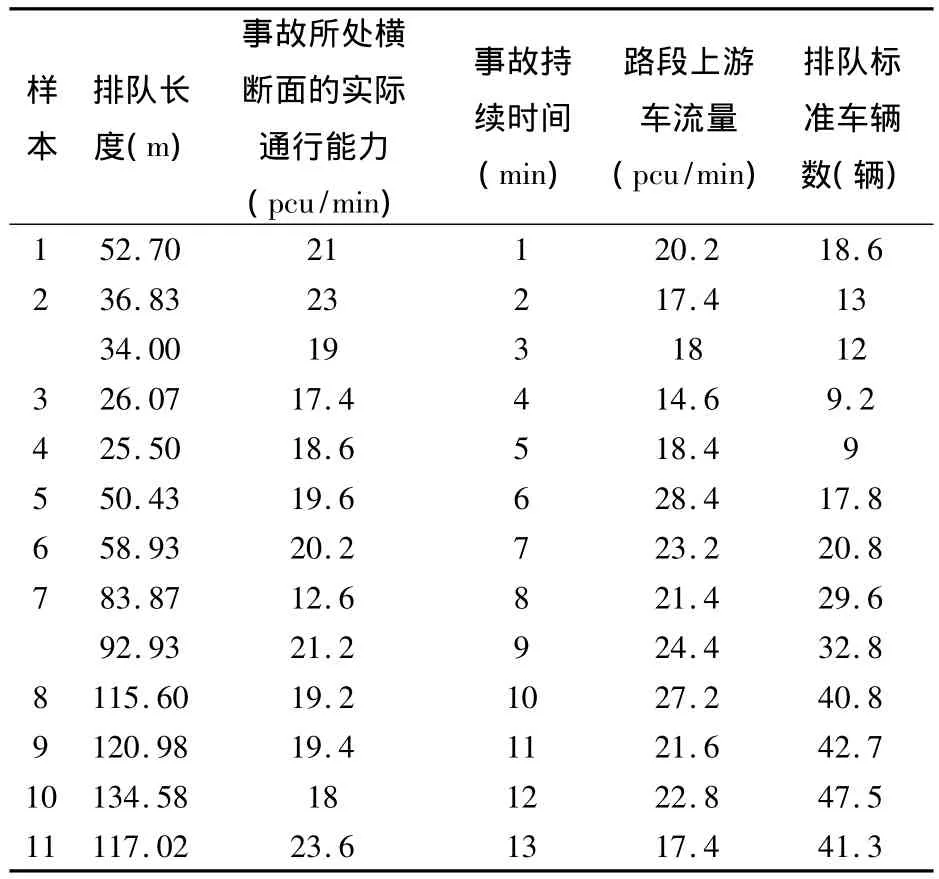
表7 堵车发生时排队长度情况表Tab.7 The queue length table in traffic jam

采用三层拓扑结构，输入层到隐含层的训练函数为Tansig，隐含层到输出层的传递函数为purelin，为了克服标准BP算法固有的一些缺陷，训练算法采用基于数值优化方法的 Levenberg-Marquardt法.使用MATLAB软件进行训练，输入层3个单元，输出层1个单元.采用反复测试的方法，用反复试验法确定隐含层的单元数为25个单元，最终即网络拓扑结构确定为3×25×1，学习速率为0.01，最大训练次数max_epoch=1000，目标误差 err_goal=0.01，附加动量因子mc=0.95时，经过587次学习后，网络成功收敛.

3.3 模型的泛化能力检验

以表7中1-8号样本输入网络模型进行训练，虽然网络的性能还没有为0，但是输出的均方误差已经很小了，MSE=0.0063，表明该网络训练速度快，效果好，网络训练误差图见图3.以9-11号样品为预测检验样本对模型泛化能力进行检验，结果见表8.

表8 BP网络模型泛化能力检验表Tab.8 The test table of generalization ability of BP network model

由表8数据可以看出，实际值与检验输出值较接近，相对误差较小平均值为3.0168% ，最大误差也只有6.9043%，表明该网络模型有较强的仿真性能，具有很好的泛化能力，能够较好的模拟交通事故路段车辆排队长度与事故横断面实际通行能力、事故持续时间的复杂关系.

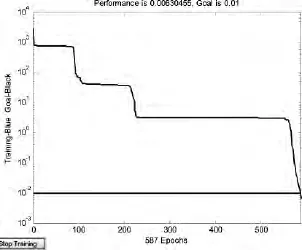
图3 BP网络训练均方误差曲线Fig.3 The mean square error curve of BP network training

4 模型的评价

(1)文章采集了大量数据，并对数据进行仿真分析，揭示了交通事故对实际通行能力的影响可转化为变道行为对实际通行能力的影响，得出变道越频繁实际通行能力越低的结论.并分析了视频1中实际通行能力随时间变化的趋势.

(2)分析了两个视频占道不同实际通行能力存在差异:先进行抽样统计，从统计学的角度利用SPSS软件提供的曼-惠特尼U检验对二者显著性差异进行科学的判断，然后从交通理论的角度结合现场实际情况对实际通行能力存在差异的原因进行分析——占用车道不同导致车辆变道行为发生率不同，使得分析具有科学性和理论依据.

(3)基于交通二流理论的思想，考虑了影响车辆排队长度的不稳定状态车流，科学地计算了车辆的排队长度，数据统计具有一定的科学性.利用统计数据建立BP神经网络模型，能够较好的模拟交通事故路段车辆排队长度与事故横断面实际通行能力、事故持续时间以及路段上游车流量的复杂关系.经检验，该模型模拟非常准确，而且对排队长度可以起到预测作用.该模型不同于传统的动力学函数模型，不需要产生复杂的函数关系式，并且方法简易，可操作性强，预测能力很好.可以推广到其他类似的工程应用领域.

［1］2013全国大学生数学建模竞赛网站［EB/OL］.［2013-09-13］.http://www.mcm.edu.cn/problem/2013/2013.html.

［2］李兵，陈小鸿.道路动态资源研究［J］.计算机工程与应用，2008，44(34):26-30.

［3］薛薇.统计分析与 SPSS的应用(第三版)［M］.北京:中国人民大学出版社，2011.

［4］姚荣涵，王殿海，曲昭伟.基于二流理论的拥挤交通流当量排队长度模型［J］.东南大学学报(自然科学版)，2007，37(3):521-526.

［5］Robert Herman，Ilya Prigogine.A Two-Fluid Approach to Town Traffic［J］.Science，1979，204(4389):148-151.

［6］Robert Herman，Siamak Ardekani.Characterizing Traffic Conditions in Urban Areas［J］.Transportation Science，1984，18(2):101-140.

［7］高爱霞，陈艳艳，荣建.基于BP神经网络技术的路段实际通行能力［J］.北京工业大学学报，2004，30(4):462-465.

［8］杨晓光，徐辉，龙科军，等.公交停靠站对相邻车道通行能力的影响［J］.系统工程，2009，27(8):74-79.

［9］孙锋，王殿海，马东方.直线型公交停靠站通行能力计算方法［J］.西南交通大学学报，2013，48(3):1-7.

［10］李松，解永乐，王文旭.AdaBoost_BP神经网络在铁路货运量预测中的应用［J］.计算机工程与应用，2012，48(6):233-234.

［11］徐黎明，王清，陈剑平，等.基于BP神经网络的泥石流平均流速预测［J］.吉林大学学报，2013，43(1):186-191.