PSO算法扰动优化策略及其收敛性研究

陶 乾，阮锦新 ，常会友，顾春琴，陈 强

(1.广东第二师范学院计算机科学系，广州510310;2.中国科学院深圳先进技术研究院，深圳518055;3.中山大学软件学院，广州510006;4.仲恺农业工程学院计算机系，广州510225)

粒子群优化(Particle Swarm Optimization，PSO)［1］算法作为基于种群的随机优化技术，通过人工种群内粒子间的合作与竞争实现了多维复杂空间内迭代搜索最优解，被成功应用于各类科学问题求解［2－4］;但其缺陷也逐渐显现，主要体现在以下3个方面:

(1)算法容易陷入局部极值，造成早熟收敛;

(2)算法在多维复杂空间的迭代进化过程有一定的惰性，解的精度难以持续提高;

(3)算法通过对自然界生物群体搜索现象的简化模拟设计而成，缺乏严格理论基础.

粒子作为PSO 算法在多维空间的搜索引擎，其行为特性直接决定了PSO 算法的优化性能.为克服局部极值，避免在进化后期收敛速度慢、精度低，各类扰动(又称为变异或跳转)优化策略常作为辅助手段来改变pBest、gBest 的引导趋势、优化粒子搜索行为、增强其在多维搜索空间的搜索能力、改进PSO算法的性能. 文献［5］采用柯西变异来改进粒子搜索性能并提出了一种新的PSO 算法;文献［6］提出了基于柯西变异的混合PSO 算法并对车辆最大允许载重进行优化;文献［7］采用柯西扰动来提升各类进化算法的优化性能;文献［8］提出了基于柯西和高斯混合变异的PSO 算法并优化支持向量机的参数选择;文献［9］提出了基于高斯跳转的高斯PSO 算法;文献［10］使用高斯扰动来优化PSO 算法并应用于经济调度;文献［11］设计出了混沌跳转的PSO 算法并对噪音问题进行了优化，文献［12］采用基于混沌时间序列的双扰动对PSO 算法进行改进并应用于网格工作流调度优化.

上述PSO 算法的扰动策略研究主要是实验验证，缺乏相关的理论分析，扰动后粒子在多维空间轨迹特性不明确，收敛性没有有效的证明，辅助优化策略缺乏理论支撑，本文从理论证明和实验验证两方面对扰动后粒子在多维空间的收敛特性进行研究.

1 双扰动下通用轨迹的收敛性

PSO 算法的pBest 和gBest 扰动的形式化定义如下:

双扰动下第i个粒子第j 维的通用轨迹公式如下:

设k=1－c1·r1－c2·r2，经递归得到

因此，轨迹形成一个序列

就级数

存在.此时，

总之，只要确保加速系数c1、c2满足0 ＜c1+c2＜4，则扰动后粒子轨迹收敛.采用扰动后，粒子跟随pBest、gBest 跳离局部最优解，重新向新的解收敛.

2 结果与分析

资源约束的项目调度问题属于NP-Hard 问题.为验证理论证明的相关结果，我们结合项目调度问题在多维空间中对随机粒子运动轨迹进行了实证分析，选用15个节点的项目调度e-Protein［12］来测试PSO 算法并验证扰动轨迹的收敛性以及pBest、gBest双扰动策略对轨迹收敛的影响. 为进一步分析随机性对粒子轨迹的影响，充分考虑了随机参数的影响r1，r2?［0，1］.所有实验的运行环境都是Pentium D 3.00 GHz，1 024 MB RAM 和Windows XP2 操作系统.

从PSO 算法的种群中随机选取粒子，在15 维优化空间绘制其3 种轨迹. 对所有维的粒子轨迹和通用轨迹进行比较，图1 清晰地给出参数设置c1+c2=1.8 +1.8 ＜4 情况下15个维度3 种不同的轨迹波形图，其中particle 代表粒子轨迹，pBest、gBest 代表pBest 轨迹和gBest 轨迹.

从图1 可见，不同的维度具有不同的迭代次数和收敛点.刚开始时，3个轨迹振荡密集，并且振荡幅度不等，随着迭代次数的增大，gBest 轨迹首先趋于稳定并收敛于一点，pBest 和粒子的轨迹随后也同gBest 轨迹一样向同一点收敛. 当gBestj(t)=，则因此，则粒子在第j 空间停止搜索并且轨迹收敛.

种群中粒子运用自己的搜索经验(pBest)和整个种群的搜索经验(gBest)，通过不断更新自己每一维的速度，搜索到新的位置，gBest、pBest 引导粒子飞行并收敛于一稳定点.其中，2、3、5、7、8、9、11、13 维度属于间隔性扰动并根据维度不同间隔时间不同，其他属于连续性扰动;连续扰动和间隔性扰动主要是根据扰动作用情况不同而不同，对粒子的收敛性影响没有明显差异.上述15个维度的整体趋势是:在扰动后粒子会出现了引导性震荡，但最后都会收敛.

下面进一步通过实验验证c1+c2＞4 情况下粒子的发散情况.通常情况下，当粒子速度vji(t+1)=0 时，粒子轨迹收敛于一稳定点.因此可通过监测迭代后期粒子速度是否接近0 来判断粒子轨迹是否发散.为更好体现粒子轨迹的动态特性，测试进行了3 000 次迭代，在同样的运行环境下独立运行20 次.同时，c1、c2每次迭代的增量定义为0.02，且c1，c2［0.1，5.8］.成功运行20 次后，从15 维中随机选取第3、11 维进行分析，如图2 所示.图中左下角深蓝色三角形表明粒子轨迹接近收敛(此时的20 次平均速度接近0). 由于粒子在20 次运行中只要一次速度不为0 则平均速度即不为0，所以我们认为只要平均速度接近0(深蓝区域)即可认为粒子在该维的轨迹收敛，否则轨迹发散.从图2 可以发现三角形区域的边弧的斜率约为－1，边界为c1+c2=4，黑色区域表明平均速度为0，粒子在扰动后经过一段时间会停止搜索、轨迹在20 次实验中完全收敛;当c1+c2＞4 时，粒子在扰动后一直高速搜索，粒子轨迹发散.因此，通过实验可以发现当参数c1+c2＞4时，粒子在受到扰动后轨迹发散.

综上分析，在gBest、pBest 双扰动下，粒子在各个维度出现了引导性震荡，维度不同振幅不同，在确保加速系数c1、c2满足0 ＜c1+c2＜4 情况下所有维度都在震荡后收敛.作为PSO 算法搜索引擎的粒子在多维空间中扰动后仍然收敛，扰动作为一种优化策略能有效提升粒子的搜索性能但不影响粒子的收敛性.总之，pBest 和gBest 双扰动作为一种优化策略能防止算法早熟收敛但不影响粒子收敛.

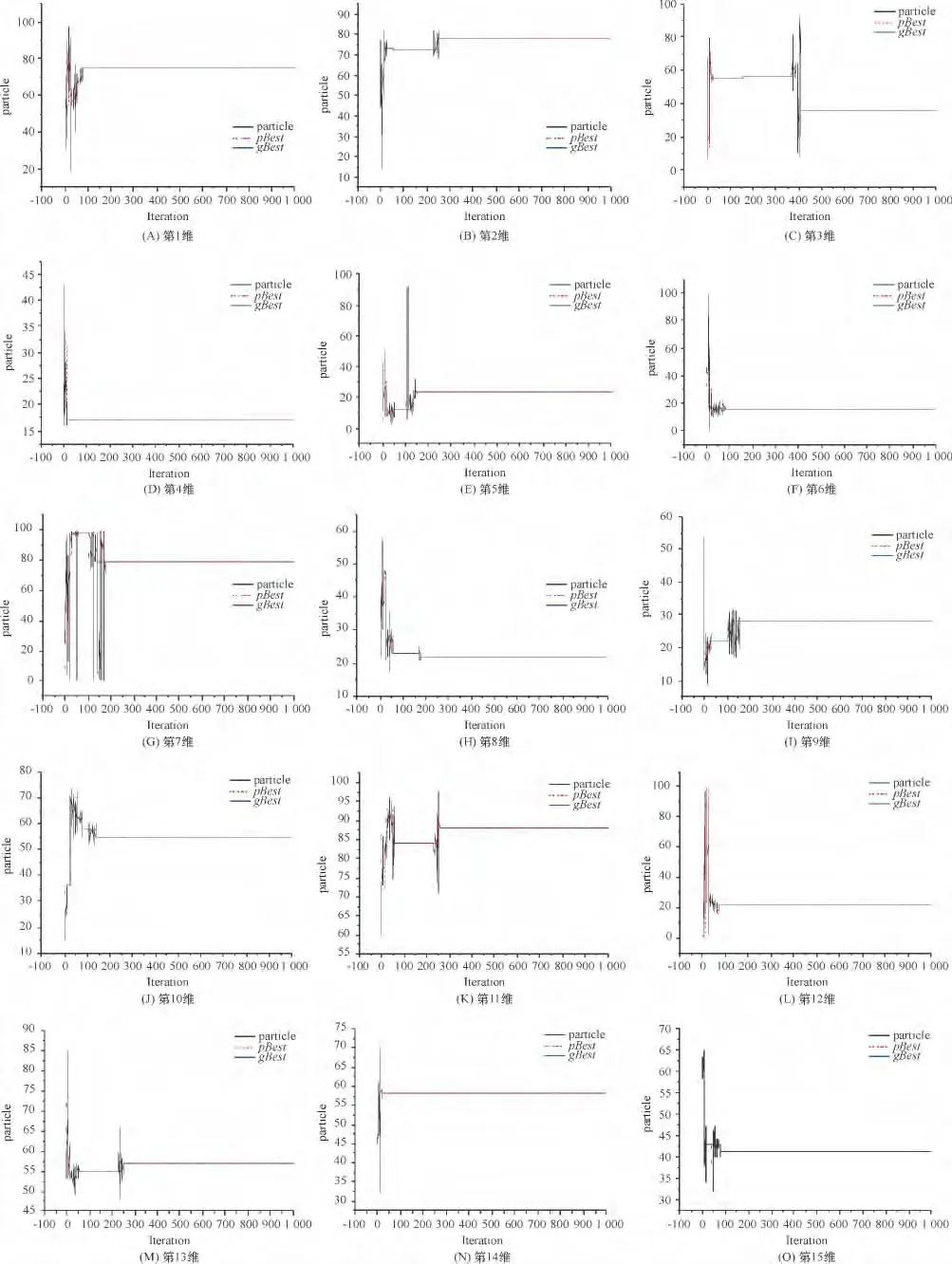
图1 扰动后粒子轨迹、pBest 轨迹和gBest 轨迹的比较Figure 1 The trajectories comparison of the particle，pBest and gBest

图2 参数c1、c2 不同取值对粒子轨迹发散和收敛影响Figure 2 The convergence of the particle trajectories under c1、c2

3 结论

本文采用递归和极限、级数收敛等数学方法对pBest 和gBest 双扰动后的轨迹收敛行为进行了分析和证明，同时在高维空间对扰动状况下粒子的收敛性进行了实验验证. pBest 和gBest 双扰动作为一种优化策略能防止算法早熟收敛但不影响粒子的收敛性.

［1］Kennedy J，Eberhart R. Particle swarm optimization［C］∥IEEE proceedings of the international conference on neural networks (ICNN). Perth，WA，1995:1942－1948.

［2］Selakov A，Cvijetinovi D，Milovi L，et al. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank［J］. Applied Soft Computing，2014，16:80－88.

［3］Khan S A，Nadeem A. Automated test data generation for coupling based integration testing of object oriented programs using particle swarm optimization［M］.New York:Springer International Publishing，2014:115－124.

［4］Gaing Z L，Lin C H，Tsai M H，et al. Rigorous design and optimization of brushless pm motor using response surface methodology with quantum-behaved pso operator［J］. IEEE Transactions on Magnetics，2014，50(1):1－4.

［5］Wang H，Li H，Liu Y，et al. Opposition-based particle swarm algorithm with Cauchy mutation［C］∥IEEE proceedings of the international conference on evolutionary computation. Singapore，2007:4750－4756.

［6］Venkatesan S，Kamaraj N，Chellam S. Optimal wheeling transaction based on maximum allowable load of the buyer bus using HPSO with Cauchy mutation［J］. International Review of Electrical Engineering，2011，6(5):2440－2447.

［7］Ali M，Pant M. Improving the performance of differential evolution algorithm using Cauchy mutation ［J］. Soft Computing，2011，15(5):991－1007.

［8］Wu Q，Law R. Cauchy mutation based on objective variable of Gaussian particle swarm optimization for parameters selection of SVM［J］. Expert Systems with Applications，2011，38(6):6405－6411.

［9］Wang X，Wang H B，Liu H T. An improved Gaussian mixture model based on least-squares cross-validation and Gaussian PSO with Gaussian jump［C］∥IEEE proceedings of the international conference on machine learning and cybernetics (ICMLC). Xi'an，China，2012，2:714－719.

［10］Varma S C，Murthy K S L，SriChandan K. Gaussian particle swarm optimization for combined economic emission dispatch［C］∥IEEE proceedings of the international conference on energy efficient technologies for sustainability(ICEETS). Nagercoil，India，2013:1336－1340.

［11］Mendel E，Krohling R A，Campos M. Swarm algorithms with chaotic jumps applied to noisy optimization problems［J］. Information Sciences，2011，181(20):4494－4514.

［12］Tao Q，Chang H，Yi Y，et al. A rotary chaotic PSO algorithm for trustworthy scheduling of a grid workflow［J］.Computers ＆ Operations Research，2011，38(5):824－836.