弯曲波反演渗透率方法研究

刘西恩，孙小芳

（中海油田服务股份有限公司油田技术事业部，北京101149）

0 引 言

获取渗透率的方法很多，主要有岩心分析渗透率、测井解释渗透率、核磁共振渗透率以及斯通利波渗透率等，这些方法有利有弊［1－4］。用多种方法获得的渗透率互相对比和验证，更可靠更准确地获取地层渗透率。

1974年，Rosenbaum［5］发现渗透率与井孔斯通利波关系密切。1987年，王乃星等［6］对利用斯通利波衰减计算渗透率进行了研究。1991年，Tang等［7］提出简化Biot－Rosenbaum模型，实现了渗透率快速反演［8］。1995年，伍先运等［9］用完 整的 Biot－Rosenbaum模型研究利用斯通利波衰减信息估算渗透率的反演方法，进一步通过泥质分析提出了对非渗透性固有衰减进行修正的方案，并给出实例。高坤等［10］和杨雪冰［11］分别实现了 Tang等提出的利用斯通利波中心频率移动以及中心时间滞后来反演渗透率的方法。为比较符合储层描述尺度和反映更大探测深度的原状地层渗透性，开展了关于偶极弯曲波反演渗透率的基础工作。王克协等［12］研究发现偶极弯曲波的衰减与孔隙地层的渗透率密切相关。马俊［13］在前人基础上，通过全波模拟和分波模拟弯曲波，研究了利用弯曲波的衰减反演渗透率的可行性。谢馥励［14］考察了偶极弯曲波的频散和衰减对地层渗透率的影响，证实了弯曲波的衰减对渗透率更加敏感，指出了弯曲波反演渗透率的可行性。本文以各向同性饱和流体孔隙介质充液井孔中声场传播理论为基础，利用偶极声波测井资料中弯曲波衰减反演得到了地层渗透率，总结提出利用弯曲波反演渗透率处理步骤，并对实际测井资料进行了处理，验证了利用弯曲波反演渗透率的可靠性。

1 利用弯曲波反演渗透率的理论基础

1．1 弯曲波正演

根据各向同性饱和流体孔隙介质充液井孔中声场传播理论可知，当n＝0时为单极源激发的声场，用分波算法可得到

式（1）描述了沿井传播的3个分波，即纵、横波滑行波及模式波，它们分别对应式（1）中的PP、PS和第3项留数部分；F（ω）为声源函数；ω为角频率；kz为轴向波数。类似单极点源情况，把偶极频域场可写为

这里角标1指n＝1，对应偶极场。前2项代表临界折射纵波和折射横波，后1项求和代表导波，即为弯曲波。这里的Nn（kz，ω）隐含包括式（2）中的第3部分为所要求取的留数。为此，只要求出不同ω对应的留数，再对其进行一维傅里叶逆变换就可模拟出弯曲波的波形。其具体计算步骤为

（2）根据留数计算公式可知

1．2 衰减的计算

频率域下全波表示为

式中，U（kz，ω）与声源结构有关，这里取

模式波的振幅由极点留数给出

将kz（ωi）＝iα（ωi）＋ki代入式（5），对第1阶模式可得

式中，α（ωi）即为弯曲波的衰减。

为去掉F（ω）和U（kz，ω）的影响，作不同z的振幅比，设

将式（7）与式（8）作比值，得到

从而得到弯曲波的衰减为

1．3 弯曲波反演渗透率

用Ai代表从实测全波截取的远近道弯曲波的模拟衰减值，以Ai作为样本函数。其中i＝1，2，…，N是频率采样点序数。用Gi（κj）代表当渗透率为Kj时由模式波极点留数计算的相应2道衰减值，以Gi（kj）作为理论模型函数，其中i＝1，2，…，N是频率采样点序数，j＝0，1，2，…为最小二乘反演迭代次数。利用线性化最小二乘法反演，构造平方误差函数使Q值最小时，对应的渗透率K值即为所要求的渗透率值。为此求并令其等于0，可得渗透率迭代公式

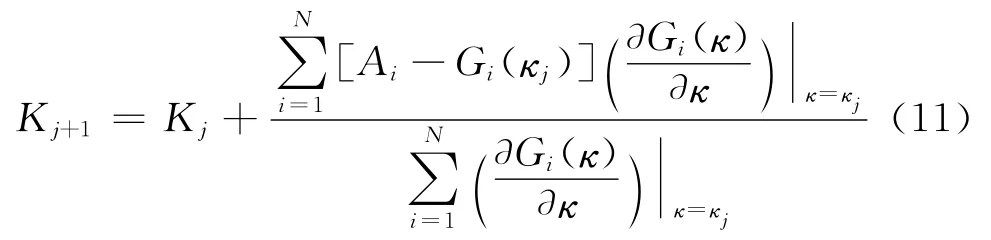
式（11）为线性化最小二乘法反演渗透率的理论公式。设置相应的精度，若满足精度，则结果为地层渗透率的反演值，若不满足则进行下一次迭代。

2 利用弯曲波反演渗透率的处理步骤

利用偶极声波测井资料中的弯曲波衰减反演渗透率包括2方面：①弯曲波的正演；②地层渗透率的反演。具体包括8个步骤。

（1）对原始弯曲波数全波数据、井径及计算的孔隙度、密度、地层纵横波速度等井内信息进行提取。

（2）计算地层骨架和孔隙流体等的弹性参数。

（3）选取一个渗透率值，分别计算各个频率点所对应的波数和留数。

（4）将求得的留数乘相关系数，得到模拟弯曲波的振幅，选取2个不同的源距得到其相应的幅度比。

（5）计算得到模拟弯曲波的衰减。

（6）由地层横波速度计算每一个深度采样点上每一个接收器的横波到时，截取3～4个周期作为实测数据的弯曲波部分。

（7）将在时域下截取到的弯曲波部分进行傅里叶正变换，选取不同源距的2道，取其模求其比值，得到实测波形的幅度比。

（8）计算求得实测弯曲波的衰减，利用最小二乘原理，Q值最小时对应的渗透率值即为所要求的渗透率值。

图1为利用某井深度采样区域对应的孔隙度、密度、纵横波速度等地层参数所模拟的8道弯曲波波形。求其频谱，选取源距相差较大的第1道与第8道作衰减曲线，并与之前所求留数时求取的衰减作对比（见图2）。

从图2中截取其中2～6kHz频率段，并作第1道与第8道的频谱曲线（见图3）。可见对实际波形处理过程中，在主频附近的能量强，求取的衰减曲线相对较准确。通过模拟弯曲波波形所得频谱计算求得的衰减曲线，与理论模拟衰减曲线相关性较好。从图3中可以看出数值模拟的弯曲波衰减和实测衰减曲线一致性越好，反演渗透率越可靠。

图1 数值模拟弯曲波波形

图2 2种衰减对比图

图3 衰减曲线与频谱对比图

3 实际资料处理分析

图4为×井砂泥岩地层中弯曲波反演渗透率与岩心渗透率、测井解释渗透率以及斯通利波渗透率综合对比图。图4中第1道砂岩对应的自然伽马值一般较低，自然电位负异常；第4道为各种方法所得到的渗透率对比结果，其中弯曲波渗透率和斯通利波渗透率进行了岩心刻度。从解释孔隙度看，孔隙性较好，具有一定的储集性，但是物性不同。其中1、2、3号层物性较好，孔隙度较大，均大于10个孔隙度，而4、5号层位孔隙度较差，都低于7个孔隙度，物性相对也较差。其中的2、3、5号层解释渗透率以及岩心渗透率和斯通利波的一致性较好，而4号层，从已有的核磁共振数据处理结果显示，该层位不存在渗透性，而斯通利波和弯曲波反演的结果反映了一定的渗透率，结合该深度位置处的STARII电成像资料，表明该深度段发育裂隙，这也揭示了产生这种差异的原因。总体看，弯曲波渗透率与岩心渗透率、测井解释渗透率和斯通利波反演渗透率变化趋势大体一致，有较好的一致性，具有划分储层的作用。

图4 ×井弯曲波反演渗透率与其他计算渗透率对比图

4 结 论

（1）弯曲波渗透率与岩心渗透率、解释渗透率和斯通利波渗透率对比发现，它们之间具有相似的变化趋势，而这4种渗透率是根据不同的物理原理和测量方法得到的，因此它们之间的吻合也说明所得到的渗透率曲线的可靠性和正确性。

（2）利用偶极声波测井资料中的弯曲波衰减反演渗透率包括弯曲波正演和地层渗透率反演2个方面。

（3）使用弯曲波反演的渗透率曲线与岩心和常规曲线反映的储层性质吻合，和其他渗透率结果具有较好的一致性，其结果能满足现场工程的应用。

［1］吴都，张超谟，王英伟，等．评价低渗透率砂泥岩岩心渗透性的方法研究［J］．石油天然气学报，2012，34（2）：80－83．

［2］陈刚，潘保芝．利用斯通利波反演地层渗透率［J］．吉林大学学报：地球科学版，2010，40（增刊）：77－81．

［3］王光海，李高明．用核磁共振测井确定渗透率的原理和方法分析［J］．测井技术，2001，25（2）：101－104．

［4］黄希君．榆树林油田葡萄花油层测井解释渗透率方法研究［J］．大庆石油地质与开发，2002，21（3）：76－78．

［5］Rosenbaum J H．Synthetic Micro－seismograms：Logging in Porous Formations［J］．Geophysics，1974，39：14－32．

［6］王乃星，杜斌，杜刚．根据斯通利波衰减计算地层渗透率的研究［J］．测井技术，1987，11（4）：26－33．

［7］Tang X M，Cheng C H，Toksoz M N．Dynamic Permeability and Borehole Stoneley Waves，a Simplified Biot－Rosenbaum Model［J］．J Acoust Soc Am，1991，90：1632－1646．

［8］Tang X M，Cheng C H．Fast Inversion of Formation Permeability from Stoneley Wave Logs Using a Simplified Biot－Rosenbaum Model［J］．Geophysics，1996，61：639－645

［9］伍先运，王克协，郭立余，等．利用声全波测井资料求取储层渗透率的方法与应用研究［J］．地球物理学报，1995，38（增刊1）：224－231．

［10］高坤，陶果，王兵．利用斯通利波计算地层渗透率的方法及应用［J］．测井技术，2005，29（6）：507－510．

［11］杨雪冰．斯通利波反演储层渗透率的方法研究［D］．杭州：浙江大学，2008．

［12］王克协，马俊，伍先运，等．利用偶极声测井中弯曲波反演渗透率的方法研究［C］∥地球物理年会，1997．

［13］马俊．井孔声波理论分析与复杂储层单、多极声测井正反演研究［D］．长春：吉林大学，1998．

［14］谢馥励．利用偶极弯曲波求取孔隙VIT介质各向异性渗透率的正、反演研究［D］．长春：吉林大学，2006．