痕迹检验中步长与足长的数学关系探究
2014-12-13胡凯许伟良胡源敏
胡凯 许伟良 胡源敏
(1.江西省赣州市公安局章贡分局刑事科学技术室,江西赣州 341000;2.浙江省绍兴市上虞区公安局刑事科学技术室,浙江绍兴 312300)
痕迹检验中步长与足长的数学关系探究
胡凯1许伟良2胡源敏1
(1.江西省赣州市公安局章贡分局刑事科学技术室,江西赣州 341000;2.浙江省绍兴市上虞区公安局刑事科学技术室,浙江绍兴 312300)
目的:发现步长与足长的数学关系,运用于现场勘查与分析中。方法:基于公式H=5.5X+32.5(H是身高,X是足长),通过对实验样本的足长预测,利用散点图与步长进行分析。结果:通过计算机的自动计算,得到步长(s)与足长预测值(x)的数学关系S=6.925X-100.1。结论:可以逆向运用一元线性回归方程S=6.925X-100.1,以达到判断人身特性的目的。
步长 足长 身高 数学关系
1 引言
在人体结构形态固有特性制约下的足或足着物与承痕体接触所留的痕迹称为足迹。足迹作为犯罪现场经常出现的一类痕迹物证,具有极高的利用价值。在分析案件时,利用足迹不但能分析作案时间、作案人数、案件性质等,还能分析犯罪嫌疑人的自然条件,例如身高、年龄、性别、体态、职业特点、行走特点、社会背景等。有利于为侦查工作提供方向,缩小排查范围,确定重点。在特定条件下还能认定人身,为诉讼和法庭审判提供证据。但是,长期以来,我国足迹检验技术一直得不到大规模推广和应用,严重影响了足迹检验技术理论的发展和实践运用。这与我们对于足迹的量化研究不足有关。本文利用前辈们留下的数据和理论成果,进一步探讨步长和足长的数学关系,为判断犯罪嫌疑人的身高提供依据。
2 实验部分
2.1 实验原理
运用公式分别计算预测值和散点图分析方法对数据进行归纳与总结。
2.2 实验方法
(1)在已知每个实验样本身高的前提下,通过公式H=5.5X+32.5[3](H是身高,X是足长)换算,得到实验样本的足长预测值X。
(2)将每个实验样本的步长S和对应的足长预测值X嵌入到散点图中,利用计算机自动计算出回归方程。
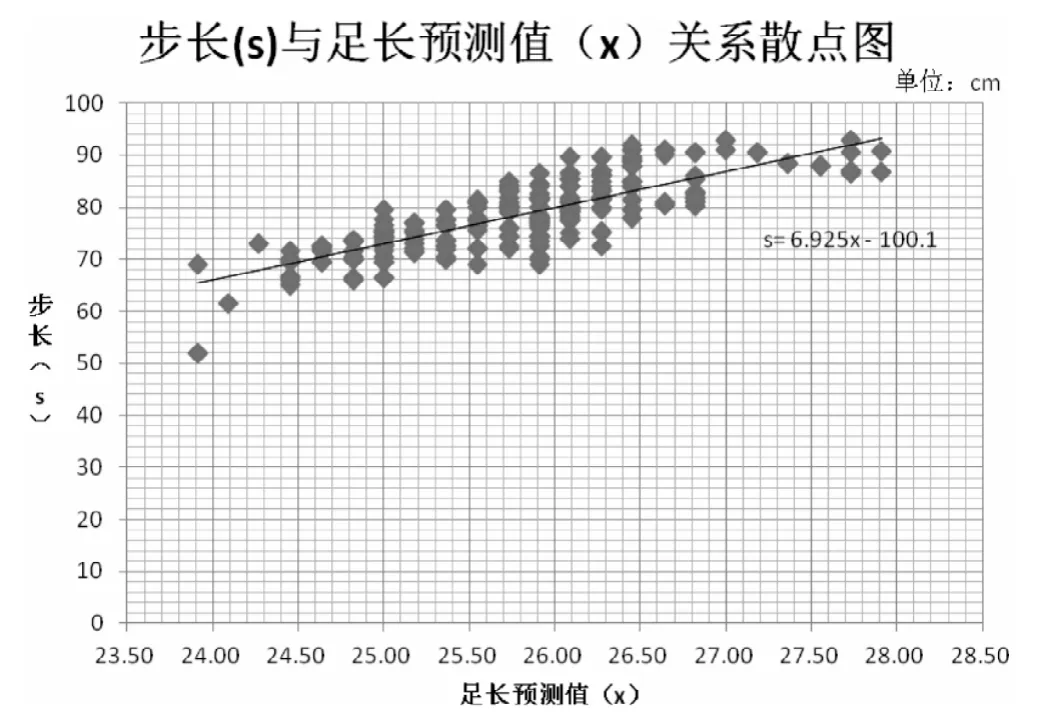
图1
2.3 实验样本的选取
2.3.1 选取的依据
我国是一个人口大国,不仅地域范围大、民族多,而且杂居覆盖面广。随着我国经济的快速发展,人口流动性强的特点也日益凸显。人口流动频率的加剧使之前部分足迹分析工作者所提出的根据地域划分(例如华北、华南等)、职业划分(例如渔民、农民等)、地理环境划分(例如山区、平原)而设定不同的系数或换算公式已经不再适用。而现在急需的是能适应各种背景人群的通用计算方法。由于人的生理结构决定了人的行走运动规律,而人的生理结构及在一定条件下形成的行走动力定型不会轻易发生变化,所以在正常行走条件下,一个人的步长基本上是稳定的,足长在成年后几乎不变,且步长和足长与其身高之间存在一定的内在关系。
运用统计方法是分析各种足迹的主要方法,一个人的身高在一天内的不同时间段不是一个固定值,而是在一定范围内变化,因此身高分析本身就应该是一个一定范围内变化的值。
2.3.2 样本的选取
为了确定步长与身高的具体关系,这里随机抽取了264名18岁-25岁之间,身高164cm-186cm之间,行走正常的人为实验对象,并让实验对象在平坦地面上正常行走,测其左、右步长(即沿步行线方向前后相邻的两枚左右足迹相应部位之间的距离),各测2-4次,然后取平均值,得到其步长。
2.4 实验结果与结论
通过计算机自动导入形成如下步长(S)与足长预测值(X)关系散点图:(如图1)
可以发现,所有散点几乎都分布在一元线性回归方程S=6.925X-100.1周围。所以,可以推断实际步长与足长存在一定的数学关系,且这种关系可以进一步运用到现场勘查分析中。尤其在犯罪现场,当客观条件不具备直接用足长分析身高的时候,我们可以逆向运用一元线性回归方程S=6.925X-100.1,先通过步长来换算出足长,进而测算出身高,以达到判断人身特性的目的。
2.5 讨论及分析
(1)在实际警务实践中,应充分结合具体案情进行综合分析,包括现场的环境、犯罪嫌疑人的心理状态等,通过分析现场足迹形成的条件辨明是否有伪装迹象。人的一切都是在大脑支配下进行的,案犯在作案时和作案后,其行为均受心理状态所支配。在作案的全过程中,其心理变化较复杂。随着心里的不断变化,其行走习惯必然出现相应的变化,这包括足与地接触面得大小和步长的长短。
(2)需要强调的是,对于换算得到的数值不应作为最终数值照搬照抄,而应该以此数值的左右3厘米或5厘米来确定一个合理的身高范围来作为参考。在由相关公式或方法估算出大致范围,可以运用本文所推荐的公式对身高进行预判,减小误差,将换算结果作为确定侦查方向的依据,缩小侦查范围,更好的为侦查破案服务。
(3)足迹学不是一门孤立的学科,而是具有广泛而深厚的相关学术基础的学科。必须将其放在物证技术学、侦查学、犯罪学、数学、心理学、气味学等社会科学、自然科学与思维科学相关学科的大系统中作整体和动态的考察,才能够保证足迹分析应用所具有的较好的广度与深度以及较高的信度与效度。
[1]李烽,段冶,郭白日呼.论足迹的特殊性[J].中国人民公安大学学报(自然科学版),200(03):20-21.
[2]姚力,高以群,王辉,吕晓森,田立新.利用步长分析身高的实验研究[J].刑事技术,1999(1):17-19.
[3]傅晓海,王森.足迹学研究课题归纳[J].贵州警官职业学院学报,2010(1):61-63.
[4]李烽.足迹统合论[M].湖北:湖北省公安专科学校编,1988年版.
