基于期望造价的建筑场地填土边坡优化设计模型

李远耀，唐朝晖，刘忠臣

(1.中国地质大学(武汉)地质调查研究院，湖北武汉 430074;2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

填土边坡因受边坡稳定性、工程造价和建设效益等多种因素影响，开展优化设计，合理选择填土边坡坡角，对于边坡安全及其风险评价尤为重要。

国内外许多学者从工程力学、边坡安全和期望造价等不同角度，提出了一些填土边坡优化设计模型或技术思路［1～4］，并应用于道路路堑、露天矿山和机场高填方的边坡设计之中［5～8］。然而，针对建筑场地平整工程中填土边坡优化设计的研究成果较少，当前工程中多采用经验设计坡角，或者根据场地周边条件给定设计坡角，具有一定的风险和主观性。

场地工程填土边坡一般具有如下特点:建筑场地具有红线范围，填土边坡坡角决定了有效建筑用地面积和建设效益;填土边坡的稳定性受到填土强度、场地高程、设计坡角和支护方案等多种因素控制;场地区的挖填平衡、低造价和高收益是场地工程优化设计的基本要求。为此，本文探讨了在填土边坡稳定条件下，以最小期望造价为目标函数，如何开展填土边坡的优化设计，并确定安全合理的填土边坡坡角。研究结果对于指导矿山环境恢复和土地整理工程具有实际意义，可为场地工程填土边坡优化设计提供实用模型和风险评价的理论依据。

1 填土边坡优化设计模型

优化设计通常指从多种方案中选择最佳设计方案，以达到最优目标。可将其概括为一个数学函数的构建-求解过程:建立相应目标函数，选择设计变量，在满足各种约束条件下，选择出现有工程条件下的最佳方案(图1)。求解该函数的基本流程是:确定目标函数→选择设计变量→构建约束条件→求解最优结果。

图1 建筑场地填土边坡优化设计基本流程Fig．1 Optimization design process of fill slope in construction site

1．1 构建目标函数

目标函数是设计要达到的目标，对于场地工程填土边坡设计，应满足前述的三项基本特征要求。这里以最小期望造价为目标函数，期望造价主要由边坡工程施工造价以及边坡工程失稳时所需付出的代价(即损失)共同组成。在边坡工程失稳损失中，文中只考虑有形价值。

以单位宽度填土边坡总期望造价为目标函数值，构建分析简图(图2)。假设坡高为H(m)，设计坡角为θ(°)，填土边坡施工范围c为(0，40)。填土工程施工费用总单价为A(元/m3)，施工管理费取费率为B，填土边坡失稳后的整修费用总单价为C(元/m3);土地单价为D(元/m2)。填土边坡破坏概率为Pf，坡面方程设为f1(x)，破坏面方程为px2，总期望造价为(元)。

则，期望造价目标函数方程为:

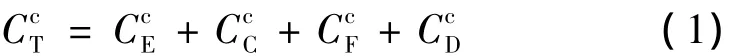
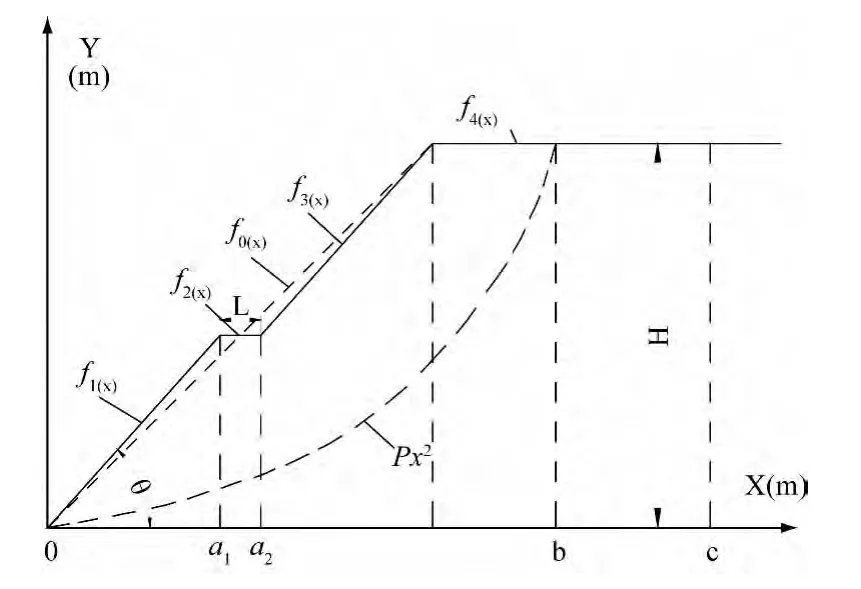
图2 单位填土边坡分析简图Fig．2 Calculation sketch of unit fill slope

CcC——边坡施工费;

CcF——边坡破坏损失费;

CcD——放坡占用土地费。

其中，CcE前期调查费可根据相关取费标准直接确定，而边坡施工费CcC、边坡破坏损失费CcF和放坡占用土地费CcD可分别由下式计算:

式中第一项为填土边坡直接施工费，为填土方量与施工单价相乘;第二项为施工管理费用，由直接施工费与相关费率相乘。

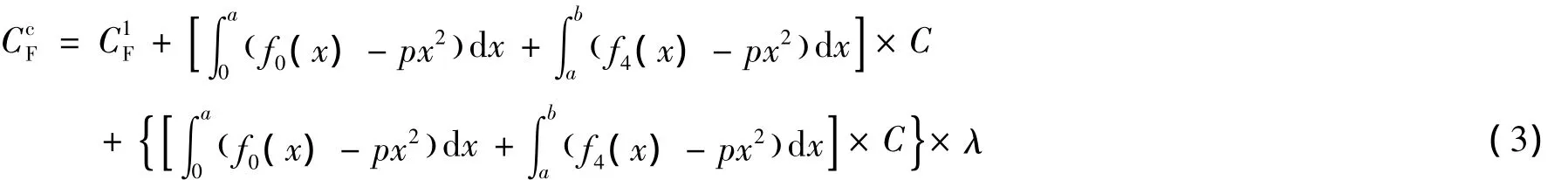
1．2 选择设计变量

设计变量为优化设计过程中需最终确定的各项独立参数。如填土边坡坡角、坡高、坡型、马道宽度等等，这些设计变量一旦确定下来，设计方案就成为明确目标。但是，设计变量越多，优化问题规模就越庞大，求解难度也越大，因此在优化设计中需要合理选择设计变量。

(1)坡高:由场地整平设计高程和原始地面高程的差值确定，后者为固定值，前者为待求设计变量。设计高程受场区最高洪水位高程、场地挖填平衡量、客土或外运土价格等诸多因素影响。要求勘查时，除测绘场区地形图，还应该收集周边洪水记录，调查客土可能性、位置、外运堆土区或周边建筑需土量等。

(2)坡角:属于优化设计中待求的关键设计变量，一般根据工程类比或经验方法确定最优坡角设计变量的取值范围。

(3)填土性质参数:填土强度与土体结构、施工方法等因素有关，其重度、密实性、强度是影响边坡稳定性和挖运价格的重要参数。在设计中应对场区自身的岩土体进行详细勘查，确定挖运土的价值、填土重度和强度等相关技术参数。建筑场地工程中，通常要求在场区范围内达到挖填平衡，填土来源一旦确定，填土性质参数可作为设计常量。

(4)其他参数:施工费、破坏损失费和占用土地费等相关的参数，与施工期间基本材料、人工单价、土地出让费和边坡破坏面形态参数p等因素有关。其中，材料人工价格和土地出让费等与当地社会经济发展水平相关，在设计期间可看作短期常量。边坡破坏面形态参数p为边坡最小稳定性系数对应的值，可采用极限平衡法试算求解，求解后可作为常量。

1．3 确定约束条件

优化设计过程中，对设计变量取值的约束限制，称为约束条件。约束条件包括填土边界范围约束、安全系数约束和变量取值范围约束。其中边界范围主要受场地的法律效应控制，即坡脚范围应在场区规划红线内。安全系数约束和变量取值范围应依据相关技术规范确定，属于优化设计工作基本内容。

(1)边坡安全约束:根据边坡设计相关技术规范的要求，如《建筑边坡工程技术规范》等，设计边坡安全等级和坡高有关，而安全系数由安全等级和计算方法确定。这里将破坏概率Pf作为填土边坡安全系数的度量指标，填土边坡对安全系数要求越高，就需要更多经济投资来降低边坡的破坏概率。根据边坡稳定性可靠度分析理论［9～10］，结合工程实际情况可确定边坡破坏概率范围，常在［0，0.1］区间内。

(2)设计坡高约束:由场地整平设计高程和原始地面线之间的差值确定，坡高与边坡安全等级有关，如《建筑边坡工程技术规范》规定，H≤10m时根据破坏后果严重性划分为三级、二级和一级边坡，10m＜H≤15m的被分为二级和一级边坡，应分别采取不同的安全系数。

(3)设计坡角约束:根据技术规范，边坡平均坡角、单级坡角与坡高、支护形式有关。当坡高小于8m时可直接选着放坡，放坡坡率通常小于1:0.75。当坡高大于8m或场地条件受限时，还需要采取支护工程确保边坡稳定，以满足边坡安全要求。

1．4 求解最优结果

求解填土边坡最优结果的基本流程为填土边坡破坏概率计算、期望造价核算及循环试算。

(1)填土边坡破坏概率:确定好初始的计算参数后，采用极限平衡方法计算边坡的稳定性系数，并通过边坡可靠度分析法计算边坡的破坏概率。

(2)期望造价核算:根据目标函数CcT和土地价格、边坡施工费单价等参数，计算满足边坡安全性约束条件下的工程期望造价值。

(3)循环试算:改变放坡坡角或坡高，并变化安全系数、支护方案等约束条件，循环上面的(1)和(2)两步，求解期望造价的最小值。将该值所对应的放坡坡角或坡高和支护方案作为优化设计的最终结果。

2 优化设计的技术要求

根据建筑场地填土边坡优化设计要求，在场地工程勘察设计中，除按技术规范进行工程部署和工程验算外［11～12］，还应注意如下的要点:

(1)一般设计只考虑工程自身造价，忽略了土地潜在价值、生态优化组合和当地经济长期发展。当设计高程等满足规范要求时，应兼顾周边区域经济发展、城市建设和生态规划的要求，当周边近期规划需要土石建筑材料或者耕土时，可适当选择较低的设计高程，使外运土石方产生价值，减少场区外部取土，保护周边区域生态。勘查时注意收集相关规划资料，与地区发展、城市建设和生态规划一致。

(2)岩土体强度参数具有空间差异和随机分布的特点，规范中多通过单一安全系数消除其随机性，虽然分析过程较简单，但并不能充分地反应边坡稳定性的不确定性。可利用破坏概率表示边坡的不确定性，但同时要满足安全系数的要求。

(3)对于填土边坡的设计方案可分为直接放坡和工程支护放坡，适用性分析时应综合考虑场地的地基基础、建筑材料、气象条件和生态恢复条件。直接放坡需论证坡面在降雨条件下抗冲刷侵蚀性、是否可进行生态护坡。

3 工程实例分析

3．1 场区边坡概况

建筑场区位于广西桂林市东南部的平乐县二塘镇，原为一座大型锰矿矿山，近年来随着锰矿资源的开采殆尽，矿山已闭坑废弃。为治理和恢复闭坑锰矿山的地质环境，并缓和平乐县经济发展与城市用地之间的矛盾，规划将闭坑的平乐二塘锰矿区改造成建设用地，对二塘镇锰矿区场地实施整平工程，因而在场区周边形成了大面积填土边坡(图3)。

首先调查周边相关规划和建设工程，区内无大型土石方工程。为此，二塘锰矿区场地整平工程需要内部达到挖填平衡，并在考虑当地最高洪水位高程的基础上设计整平高程。在整平场区边界均形成填土边坡，设计坡高在8～15m范围内。

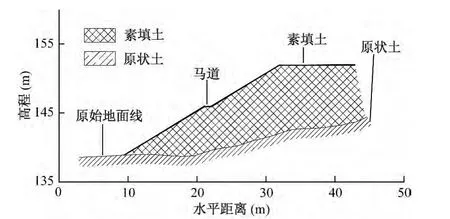
图3 平乐二塘锰矿区典型填土边坡示意图Fig．3 Typical fill slope in manganese mine，Pingle County

根据《建筑边坡工程技术规范》，矿区填土边坡属于二级边坡，选择坡率法进行治理。设计安全系数为1.25，对应的破坏概率取0～0.1。设计填土边坡分为两级，为简化计算，采用等分法放二级坡，设总坡高为H，则单级坡高为H/2。根据工程经验及当地自稳坡角，设计填土边坡的单级坡角范围值取θ(30°～60°)，马道宽度L=1m。

3．2 填土边坡相关参数

根据矿区范围内岩土体的勘查资料，利用试验数据的统计结果及当地工程经验参数，综合确定填土边坡设计参数(表1)。工程费用单价可参考相关定额标准及当地市场价格确定(表2)。

表1 填土边坡设计选取参数的统计特征Table 1 Statistical characteristics of the design parameters on fill slope

表2 填土边坡设计涉及工程费用单价表Table 2 Engineering unit-cost of fill slope

3．3 填土边坡最优化数学模型

根据上述填土边坡的设计变量、目标函数以及约束条件，构建最优化数学模型如下:

3．4 优化设计结果

利用MATLAB软件实现优化设计数学模型流程，进行填土边坡最优放坡坡角的自动搜索和验证计算。图4为程序所完成设计坡高H=10m的分析图，显示了填土边坡放坡坡角和期望造价的相关关系。设计目标为填土边坡工程单位工程造价最低，对应的最优坡角为44°，单位工程的最小期望造价为14210元。

同时，可将填土边坡各项数据进行分步计算，当坡高H=10m，坡角从30°逐一增加，可得到31组符合约束条件的数据(表3)。分步计算数据显示，当填土边坡高度为10m时，最优放坡坡角为44°，对应的最小期望造价约 14210元，与自动搜索结果相吻合。

图4 设计坡角与期望造价关系图Fig．4 Relation between design slope angle and expected cost

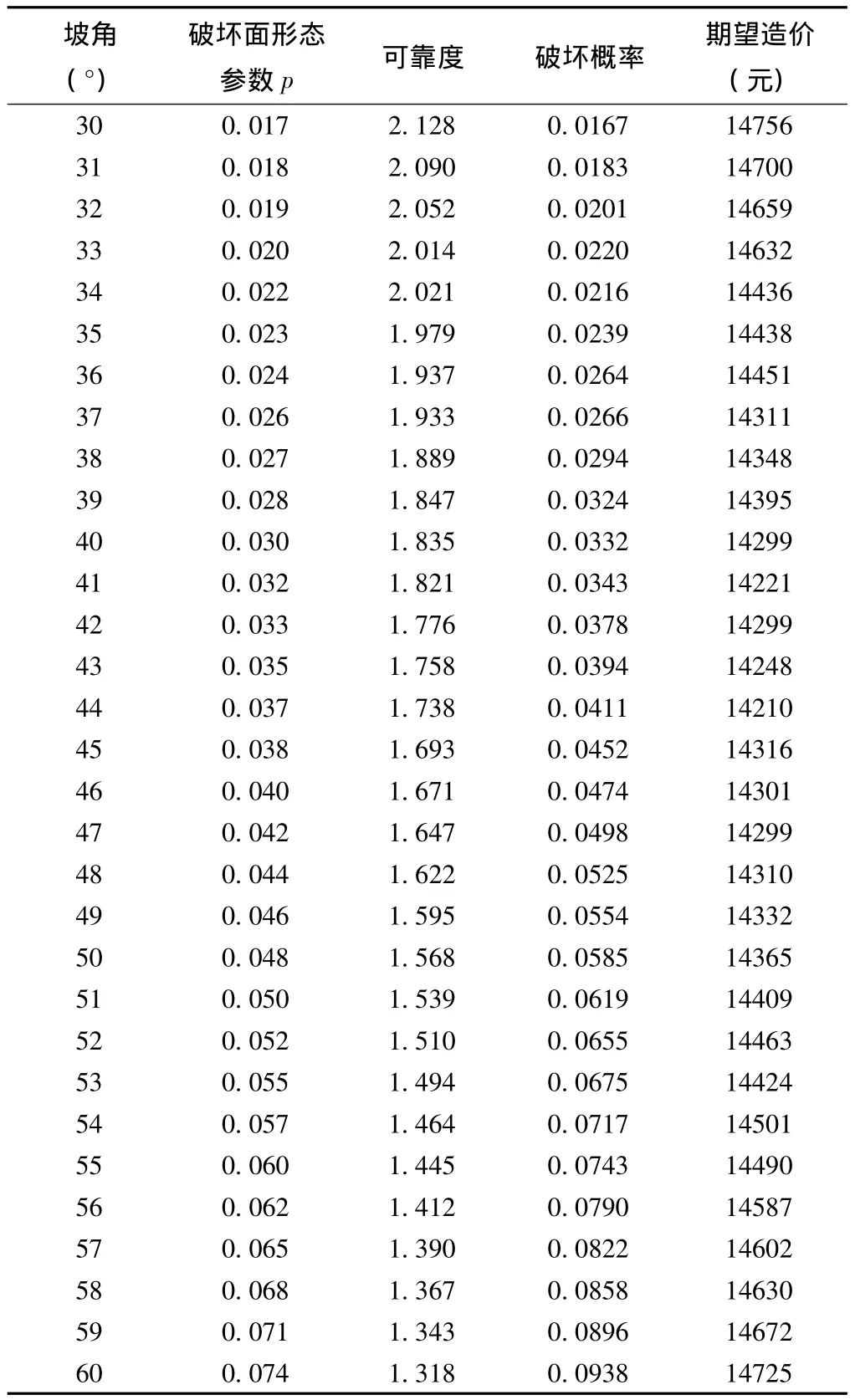
表3 高度为10m的填土边坡优化计算数据统计表Table 3 Optimization calculation data of fill soil slope with 10m height

3．5 填土边坡设计建议

利用基于期望造价的优化设计模型，对平乐二塘锰矿区设计坡高9～14m范围内，整数高程的填土边坡逐一进行最优坡角的自动搜索，可以直接得到对应高程的最优设计坡角及期望造价，结果如表4所示。

表4 9～14m范围内整数高程填土边坡计算结果统计Table 4 Expected cost and optimal slope angle of the fill slope height of 9～14m

同时发现，边坡工程造价和设计坡高呈线性正相关关系，表明设计坡高越高，工程投入经费越高;而最优坡角和设计坡高之间表现为负指数相关关系，表明随着设计坡高的增大，起初最优设计坡角会相应变小，但一定程度后将趋于平稳。针对平乐二塘锰矿区填土边坡，由于场区内废弃土方规模较大，大部分地段填土边坡高程设计值不宜小于11m，同时根据期望造价最低及建成建筑场区面积最大的基本要求，建议该填土边坡的设计坡高为12m，相应的最优坡角为31°。

4 结论

(1)基于期望造价的填土边坡优化设计模型，以最小期望造价为目标函数。其中，期望造价由前期调查费、边坡施工费、边坡破坏损失费和放坡占用土地费构成;模型主要优化设计变量为坡高、坡角、填土性质参数和破坏面形态参数;模型约束条件为场区边界范围、安全系数和变量取值范围约束。

(2)应用优化设计模型时，应在建筑场地填土边坡勘查设计过程中，注重与当地建设规划的衔接，并考虑设计参数的空间变异、随机分布和设计方案适用性。

(3)利用基于期望造价的优化设计模型，可以直接得到对应高程的最优坡角及期望造价。对于工程实例二塘锰矿区填土边坡，还发现最优坡角和设计坡高之间表现为负指数相关关系，工程造价和设计坡高之间呈正线性相关关系。在综合分析的基础上，建议该填土边坡的设计坡高取12m，最优坡角为31°。

［1］ 杨庆，焦建奎，栾茂田，等.边坡可靠性与经济风险性分析及其应用［J］.工程地质学报，2000，8(1):86-90.［YANG Q，JIAO J K，LUAN M T，et al.Reliability analysis and risk evaluation of the slope engineering ［J］.Journal of Engineering Geology，2000，8(1):86-90.(in Chinese)］

［2］ 边世斌，王琛，赵军，等.基于期望造价的黄土路堑高边坡优化设计模型［J］.西安工业大学学报，2008，28(1):81-85.［BIAN S B，WANG C，ZHAO J，et al.Optimized Design Model of Highway Steep Loess Slope Based on the Expectation Cost［J］.Journal of Xi’an Technological University，2008，28(1):81-85.(in Chinese)］

［3］ 叶万军，杨更社.基于坡面稳定的黄土路堑高边坡优化设计［J］.岩土力学，2009，30(2):531-536.［YE W J，YANG G S.Cutting high loess slope optimization design based on slope surface stability［J］.Rock and Soil Mechanics，2009，30(2):531-536.(in Chinese)］

［4］ 蔡美峰，朱青山，乔兰，等.大顶铁矿露天采场边坡稳定性分析与优化设计［J］.北京科技大学学报，2012，34(3):239-245. ［CAI M F，ZHU Q S，QIAO L，et al.Slope stability analysis and optimum design in dading open-pit iron mine［J］.Journal of University of Science and Technology Beijing，2012，34(3):239-245.(in Chinese)］

［5］ 陈金锋，宋二祥.西南山区机场高填方边坡反压护道优化设计［J］.工程力学，2012，29(6):85-91.［CHEN J F，SONG E X.Optimized design of loading berm for high fill slope of airport in mountainous area of southwest China［J］.Engineering Mechanics，2012，34(3):239-245.(in Chinese)］

［6］ 巨能攀，赵建军，邓辉，等.公路高边坡稳定性评价及支护优化设计［J］.岩石力学与工程学报，2009，28(6):1152-1161.［JU N P，ZHAO J J，DENG H，et al. Stability evaluation of high slope for highways and optimized support design［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(6):1152-1161.(in Chinese)］

［7］ 郭长宝，张永双.陕北黄土高边坡可靠度分析及边坡优化设计［J］.中国地质灾害与防治学报，2005，16(4):5-10.［GUO C B，ZHANG Y S.Reliability analysis and optimizing design of the high sandy loess slope in Northern Shaanxi［J］.The Chinese Journal of Geological Hazard and Control，2005，16(4):5-10.(in Chinese)］

［8］ 姚耀武，陈东伟.土坡稳定可靠度分析［J］.岩土工程学报，1994，16(2):80-87.［YAO Y W，CHEN D W.Analysis of reliability index in slope stability［J］.Chinese journal of Geotechnical Engineering，1994，16(2):80-87.(in Chinese)］

［9］ 唐朝晖，柴波，刘忠臣，等.填土边坡稳定性的可靠度分析［J］.地球科学:中国地质大学学报，2013，38(3):616-624.［TANG ZH H，CHAI B，LIU Z C，et al.Reliability analysis of stability of fill slope［J］.Earth Science:Journal of China University of Geosciences，2013， 38(3):616-624.(in Chinese)］

［10］ 乐超，徐超.加筋土边坡安全评价的简化水平条分法［J］.水文地质工程地质，2013，40(2):74-78.［LE C，XU C.Simplified horizontal slice method of reinforced soil slopes safety analysis ［J］.Hydrogeology＆ engineering geology，2013，40(2):74-78.(in Chinese)］

［11］ 徐春明，李文勇，陈景雅，等.某高速公路顺层路堑边坡的勘察和优化设计［J］.工程勘察，2009(4):21-25.［XU C M，LI W Y，CHEN J Y，et al.The investigation and optimum design for the bedding slope in an expressway［J］.Geotechnical Investigation ＆Surveying，2009，(4):21-25.(in Chinese)］

［12］ 唐朝晖，柴波，罗超，等.矿山地质环境治理工程设计思路探讨——以广西凤山县石灰岩矿山为例［J］.水文地质工程地质，2013，40(2):124-127.［TANG Z H，CHAI B，LUO C，et al.Design ideas of controling geo-environmental problems of mines:a case study of a limestone mine in Fengshan County，Guangxi［J］.Hydrogeology ＆ Engineering Geology，2013，40(2):124-127.(in Chinese)］