基于离散元法预测碳化硅陶瓷的高温力学性能
2014-12-11姜胜强谭援强张高峰彭锐涛
姜胜强,谭援强,张高峰,彭锐涛
(湘潭大学机械工程学院,湘潭411105)
0 引 言
陶瓷材料由于具有优良的力学性能而被广泛应用于航天、航空、发动机、机械电子等领域。以碳化硅(SiC)陶瓷为例,因其具有优良的高温力学性能以及较低的热膨胀系数、较高的热导率以及密度小等优点,而被广泛用于制造火箭发动机燃烧室内壁、喷嘴及鼻锥等重要零件[1-2]。从文献报道可知[3-5],近年来诸多研究人员针对陶瓷等结构材料的高温力学性能进行了大量试验,虽然获得了比较可靠的力学性能参数,但试验周期长,需要消耗大量的人力、物力和财力,且对于具有复杂形状的陶瓷结构件来说,受试验条件限制,难以获得其力学性能参数及高温破坏机理。
随着计算机技术及数值分析技术等的飞速发展,采用数值模拟的手段来研究陶瓷材料在不同温度下力学性能的方法得到了广泛应用。朱伟等[6]采用分子动力学法模拟了不同温度下RDX(三亚甲基三硝胺)晶体的力学性能,王超等[7]采用分子动力学法模拟了防热陶瓷材料的高温力学性能及断裂模式。
1971年,Cundall[8]首次提出了适用于岩石力学的离散元法(DEM),目前该方法已在岩石[9]、混凝土[10]和陶瓷[11-13]等材料中得到了广泛应用。离散元法起源于分子动力学,将材料视为离散颗粒的集合体,颗粒之间用键连接,用键的断裂来描述微裂纹的产生,而且模拟过程中温度具有可控性,从而使离散元法成为模拟陶瓷等脆性材料高温力学性能及高温损伤破坏过程的一种新手段。
作者基于离散元法建立并校准了碳化硅陶瓷常温下的力学性能,并建立了对块体材料离散化的热力学模型,将其引入单轴压缩及三点弯曲等试验来模拟碳化硅陶瓷在不同温度下的力学响应,并动态地观察其损伤破坏过程。
1 离散元模型的建立及校准
离散元中颗粒与颗粒之间的相互作用力由位移重叠量及相应的力-位移准则来确定,颗粒在任意时步内的运动满足牛顿第二定律。离散元法将裂纹的生成与扩展看成是颗粒与颗粒之间连接键的断裂,能直观地处理裂纹的形成与扩展过程,如图1所示。

图1 离散元模型中的裂纹Fig.1 Cracks in DEM model
为了建立与碳化硅陶瓷微观结构及力学行为相似的离散元模型,采用PFC2D[14]软件生成一个颗粒随机分布且紧密排列的颗粒粘结(BPM)模型,颗粒之间采用平行键连接。众所周知,陶瓷材料属于典型的非匀质体,晶粒尺寸大小不一,且含有随机分布的气孔和杂质。为了使离散元模型和实际材料在微观角度上相似,采用不同尺寸的颗粒来描述晶粒(最大半径与最小半径之比为1.5),并使整个模型的孔隙率与材料的孔隙率相符。除此之外,为了使所建立的离散元模型与实际材料的力学性能(如弹性模量、抗压强度、泊松比等)相匹配,需要对离散元模型中的参数(如颗粒刚度、颗粒之间的摩擦、颗粒之间的键强度等)进行反复调试和设置。目前,这些微观参数很难通过试验的方法来测试,将陶瓷材料的宏观力学性能与微观参数相匹配的方法也还在继续探索中。因此,采用数字试验校准的方法对离散元模型进行不同的试验模拟,以校准模型中的微观参数。采用单轴压缩、三点弯曲、单边切口梁等试验来校准所建立的碳化硅离散元模型[12],结果如表1所示。前述力学性能试验过程中的碳化硅陶瓷通过真空反应烧结工艺制备(碳化硅微粉粒径8~10μm,反应烧结温度1 700℃),烧结成型后的材料中含约10%(质量分数)的游离硅,其余为碳化硅。

表1 碳化硅陶瓷离散元模拟与实测主要力学性能Tab.1 Main mechanical properties of SiC ceramic in experiment and in DEM simulation
2 离散体中的热力学模型
2.1 热传导方程
在PFC2D 中,采用含有热存储器(与颗粒相关)和热管(与键相关)的微观结构模型来模拟温度场,热量在通过热存储器之间的激活热管中传递,如图2所示。热管与颗粒之间的接触同时存在,但只有在两个颗粒之间有重叠或者有连接键存在时,热管才是激活的。如果构成材料的微观模型在加载过程中有连接键产生或者断裂,都将改变激活热管的数量,从而改变材料的导热能力。

图2 PFC2D中颗粒、热存储器和热管的示意Fig.2 Abridged general view of particles,thermal reservoirs and heat pipes in PFC2D
对于连续体而言,假定物体应变的改变不会产生温度的变化,则其热传导方程为
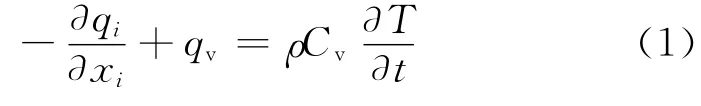
式中:qi为沿坐标轴xi方向的热流通量;qv为单位体积内的热功率密度;ρ为质量密度;Cv为材料的比热容;T 为温度;t为时间,xi为空间坐标;下标i为方向指标(i=1,2,3)。
根据傅里叶变换,可以得到连续体的热流通量与温度梯度之间的关系:

式中:kij为材料在空间方向上的热传导率张量,对各向同性材料,热传导率在各个方向上保持常数;xj为空间坐标,下标j为方向指标(j=1,2,3)。
对于离散的体系而言,需要将式(1)进行转换。假定离散体的总体积为V,单位体积内的热流通量以qi的散度来表示,在体积为V 的热存储器上qi的散度平均值为

对式(3)通过高斯差分将其转换为对面积的积分:
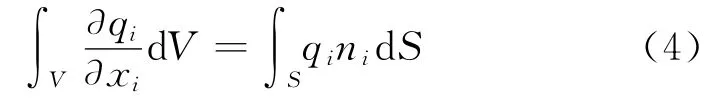
式中:ni为表面向外的单位法向矢量;S 为表面积。
假定离散体中的热量只在N个热管中发生流动,从而式(4)可以转换为
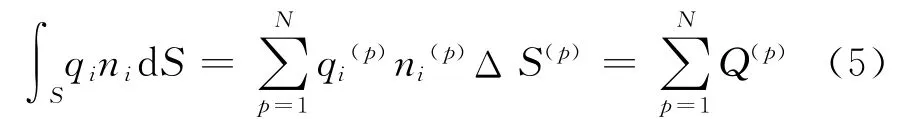
式中:上标(p)为与热管p相关的变量;Q(p)为从热存储器中流经热管p的功率;ΔS(p)为热管p的横截面积。

将式(6)代入到式(1)中,可以得到离散体的热传导方程:
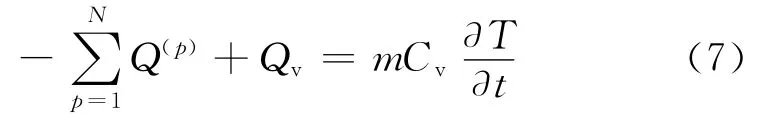
式中:Qv=V·qv,为离散体的热源强度;m 为离散体的质量;Cv为连续体材料的比热容。
如果把单个热管看作单位长度内具有热阻η的一维单元,则每个热管的功率为
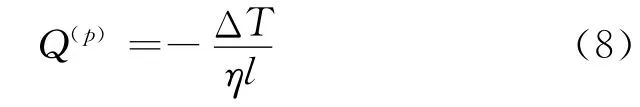
式中:ΔT 为热管两端的温度差;l为热管的长度。
2.2 热管热阻与材料热传导率的关系
在离散元中,假定单个热管的热阻为η,体系中包含N个热管,总体积为V,则在材料体积V 内的平均热流通量为

同时,热量只在热管内流通,从而上式可以转换为:

式中:A(p)为 热 管p 的 有 效 横 截 面 积;l(p)为 热 管p的长度。
热管的热流通量定义为

将式(8)代入式(11)中,可以得到:

式中:nj为热管的单位法向矢量;ΔT 为热管两端的温度差。
将式(12)、(13)代入到式(10)中,可以得到:
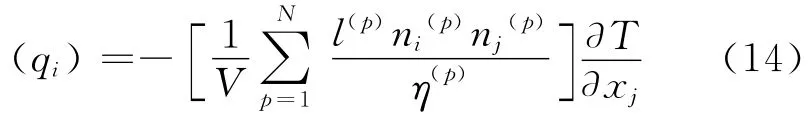
比较式(14)与式(2)可以得到在离散元体系中热传导率张量kij:
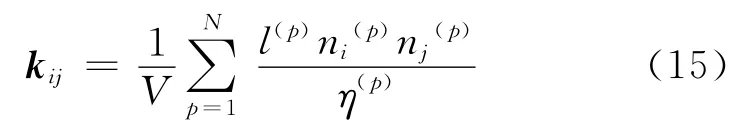
从式(15)可知,只要给定单个热管的长度、单位法向矢量、热阻以及总热管数量等参数就可以计算出离散单元所描述的材料的热传导率。
2.3 热力学耦合计算
在离散元中,材料的热应变通过颗粒以及颗粒之间连接键的热膨胀来描述,且温度引起的应变通过改变颗粒的半径来实现。给定一个温度的变化ΔT,可以计算出粒子半径R 的改变量ΔR,即:

式中:α为与每个颗粒相关的线性热膨胀系数。
如果颗粒之间存在连接键(如平行键),且热管是激活的,那么连接键的长度ˉL 将在温度变化时发生相应的改变,从而改变键的受力情况。假定在温度变化时,ˉL 的改变只影响法向力的改变,即:
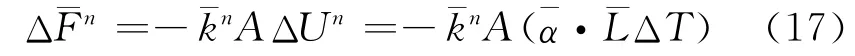
通过以上的推导可知,在离散元体系中材料的热传导率通过给定单个颗粒的热阻来确定,颗粒与颗粒之间的热传导以连接键的存在为基础,若产生新的连接键或连接键发生断裂,则将改变材料的热传导能力。热量所产生的应变通过改变颗粒的半径或连接键的长度来实现,进而引起材料内部接触力的改变。
3 碳化硅陶瓷高温力学性能的模拟与讨论
采用前面已校准的碳化硅陶瓷微观参数,通过施加不同的温度场以模拟不同温度下材料力学性能的变化,通过模拟单轴压缩试验和三点弯曲试验来获得材料的弹性模量、泊松比、抗压强度及抗弯强度等力学性能参数,模型如图3所示。单轴压缩试验中包含的颗粒数为7 486个,加载速度为0.2 m·s-1;三点弯曲试验中包含的颗粒数为10 675个,加载速度为0.1m·s-1,颗粒的平均半径为2μm,最大半径与最小半径之比为1.5。为了消除模拟的随机性所产生的误差,每个模型分别选取5个不同的随机数进行模拟,最后取其平均值作为模拟结果。模拟过程中选取9个不同的温度场(从100 ℃递增至1 700 ℃,增量为200 ℃)。
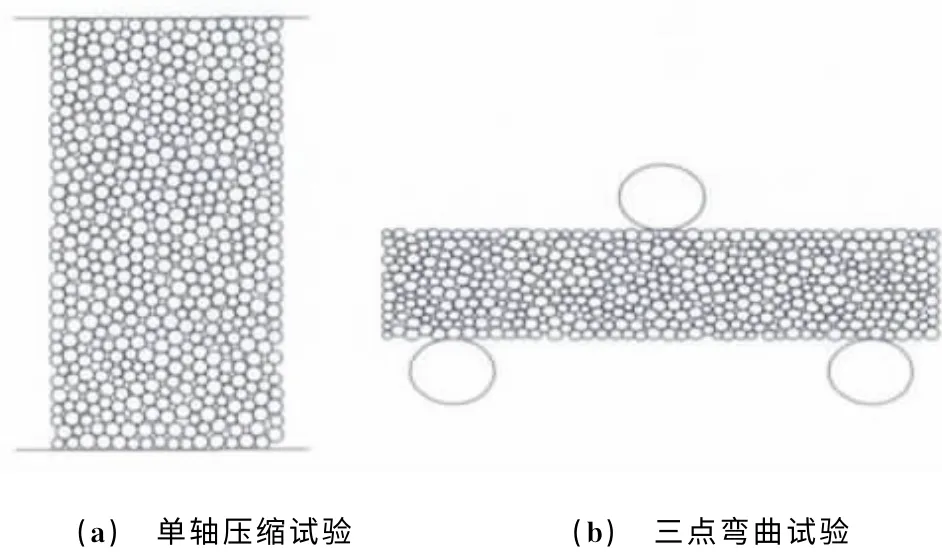
图3 离散元力学性能测试模型Fig.3 DEM model for uniaxial compression test(a)and three-point bending test(b)
3.1 温度对力学性能的影响
从图4中可以看出,当温度为100~500 ℃时,材料的应力-应变曲线基本一致,这说明在该温度区间时,温度对材料的力学性能基本没有影响。随着温度的升高,应力的峰值逐渐降低,对应的应变也相应降低,应力-应变曲线的斜率也逐渐减小,从而表明材料的弹性模量有所降低。对比高温和低温区间的失效响应曲线,可以看到材料由最开始的脆性断裂(500 ℃以下)逐渐向准脆性断裂(500~1 100 ℃)甚至塑性失效转变(如1 300 ℃)。应力-应变曲线的结果表明,温度对材料力学性能有明显的影响,随着温度的升高,材料开始出现一定程度的软化,其破坏机理也相应发生改变。
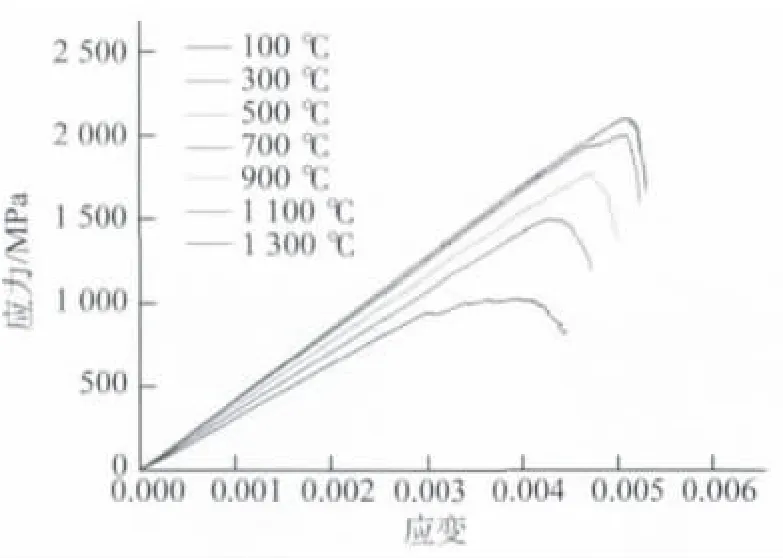
图4 不同温度下碳化硅陶瓷单轴压缩试验过程中的应力-应变曲线Fig.4 Stress-strain curves of SiC ceramic during uniaxial compression at different temperatures
由图5(a)可知,随着温度的升高,材料的弹性模量逐渐降低,泊松比逐渐增大,这表明材料的抗变形能力降低,在高温作用下发生了一定的软化现象。由图5(b)可见,温度越高,材料的抗压强度和抗弯强度越低。力学性能随温度的变化曲线同样表明,在温度低于500℃时,材料的力学性能变化较小,而温度一旦持续升高后,其力学性能将发生明显的改变。

图5 碳化硅陶瓷力学性能随温度变化的模拟结果Fig.5 Simulated results of mechanical properties as a function of temperature for SiC ceramic:(a)elastic modulus and Poisson′s ratio and(b)compressive strength and bending strength
3.2 不同温度下材料的破坏形态
由图6可见,当颗粒之间的连接键所承受的外载荷大于键本身的强度时,连接键发生断裂,此时便认为是新微裂纹产生了。若一系列的微裂纹连接形成曲折的裂纹路径时,宏观裂纹便产生了。图6中的白色线段表示裂纹,可见当温度较低(低于500 ℃)时,裂纹形成的材料损伤线与底面成45°~50°的夹角,从而表明此时碳化硅陶瓷的破坏形态以脆性断裂为主;随着温度升高(如700,900℃),裂纹的扩展趋势出现了一定变化,部分裂纹汇合形成的局部宏观裂纹不再与底面成45°~50°的夹角,但材料的破坏形态依然以脆性断裂为主;当温度升至1 100 ℃以上后,裂纹的扩展不再有明显的规律,且在试样中间有“墩粗”的迹象,说明此时材料的破坏机理不再是以脆性断裂为主,而是呈现了一定的塑性变形,且在高温作用下材料出现“墩粗”现象。

图6 不同温度下碳化硅陶瓷单轴压缩破坏后的形貌Fig.6 Failure morphology of SiC ceramic after uniaxial compression test at different temperatures
4 结 论
(1)建立了脆性材料的离散元热力学模型,给出了材料微观热力学参数与宏观热力学参数之间的关系。
(2)建立并校准碳化硅陶瓷材料的离散元模型,模拟了在不同温度下材料的单轴压缩试验及三点弯曲试验;当温度小于500℃时,温度场对材料的力学响应及力学性能参数基本没有影响,但随着温度的逐渐升高,材料的弹性模量逐渐降低,泊松比逐渐增大,抗压强度和抗弯强度也随之降低。
(3)结合材料的应力-应变曲线、力学性能参数以及不同温度下的单轴压缩破坏形貌可知,随着温度的升高,材料的破坏形态由脆性断裂逐渐向塑性变形转变,并会使材料出现一定的软化现象。
[1]OHRING M.Materials science of thin films:deposition and structure[M].Singapore:Academic Press,2006.
[2]DING Y,NORTHWOOD D O,ALPAS A T.Fabrication by magnetrnn sputtering of Al-Cu-Fe quasicrystalline films for tribological applications[J].Surface and Coating Technology,1997,96:140-147.
[3]刘孝福,娄延春,苏贵桥,等.定向凝固用陶瓷型壳高温力学性能研究现状[J].特种铸造及有色合金,2010,30(10):913-917,983.
[4]黄小萧,温广武,程显明.A14SiC4陶瓷的高温抗氧化性能和高温力学性能的研究[J].材料工程,2004(12):32-35.
[5]白世鸿,乔生儒,舒武炳,等.先进结构陶瓷高温力学性能测试与表征[J].材料工程,2000(10):45-48.
[6]朱伟,肖继军,马秀芳,等.不同温度下RDX 晶体力学性能的MD模拟[J].火炸药学报,2007,30(4):17-19,24.
[7]王超,梁军,栾旭.防热陶瓷材料高温力学性能及断裂模式的分子动力学模拟[J].材料工程,2008(增1):239-242.
[8]CUNDALL P A,STRACK O D L.A discrete numerical model for granular assembles[J].Géotechnique,1979,299(1):47-65.
[9]HUANG H.Discrete element modeling of tool-rock interaction[D].Minnesota:University of Minnesota,1999.
[10]HZENTZ S,DONZE F V,DAUDEVILLE L.Discrete element modeling of concrete submitted to dynamic loading at high strain rates[J].Computers and Structures,2004,82:2509-2524.
[11]姜胜强,谭援强,聂时君,等.碳化硅陶瓷预应力加工的离散元模拟 与 实 验 研 究[J].无 机 材 料 学 报,2010,25(12):1286-1290.
[12]TAN Yuan-qiang,YANG Dong-min,SHENG Y .Discrete element method(DEM)modeling of fracture and damage in the machining process of polycrystalline SiC[J].Journal of the European Ceramic Society,2009,29:1029-1037.
[13]TAN Yuan-qiang,YANG Dong-min,SHENG Y .Study of polycrystalline Al2O3machining cracks using discrete element method[J].International Journal of Machine Tool & Manufacture,2008,48:975-982.
[14]CUNDALL P A.PFC2D user′s manual[M].Version 3.Lakewood,Colorado,USA:Itasca Consulting Group Inc,2002.
