导管架管节点裂纹的断裂评估和疲劳评估方法
2014-12-11尹彦坤
尹彦坤
(湛江南海西部石油勘察设计有限公司,广东 湛江 524057)
导管架管节点裂纹的断裂评估和疲劳评估方法
尹彦坤
(湛江南海西部石油勘察设计有限公司,广东 湛江 524057)
目前海洋油气研究中对导管架管节点的疲劳设计和校核,主要采用应力-寿命(S-N)曲线的方法,断裂力学方法的研究和应用较少。系统地介绍了断裂力学的基础理论、ECA评估、裂纹扩展率以及管节点评估方法和流程。最后通过应用JPEFA软件进行的评估实例,介绍了评估过程。
海洋油气工程; 管节点; 疲劳; 断裂力学; ECA
0 引 言
疲劳破坏一直被认为是海洋工程结构的主要的破坏形式之一。其主要表现是海洋平台长期受到波浪的反复作用,结构出现裂纹并逐步扩展,最后在低应力下产生脆性断裂。导管架的管节点在焊缝处容易出现高度的应力集中,因此管节点成为疲劳破坏的关键位置。
导管架在设计阶段对管节点疲劳的控制是采用基于应力-寿命(S-N)曲线和Palmgren-Miner 线性累积损伤的方法,并给予一定的安全系数。S-N曲线是对标准试件进行疲劳试验得出的,S对应热点应力幅值,N为试件对应S的循环次数。导管架承受的每个波浪荷载工况引起的微破坏通过Palmgren-Miner法则进行线性累加,从而进行疲劳寿命的预测。
S-N曲线法适用于裂纹生成寿命占整个疲劳寿命主导地位的情况。当结构的任何部位出现裂纹后,裂纹在交变载荷作用下能否扩展或者扩展速率的大小就取决于裂纹尖端的应力场强度。对已有裂纹的结构的疲劳寿命评估,采用断裂力学的方法更为合适。
本文重点介绍管节点张开型裂纹的断裂疲劳评估理论依据,并研究从设计环境条件生成评估输入数据(热点应力幅、节点局部应力)的方法。
1 管节点的热点应力
导管架管节点是连接各个构件的关键部位。管节点类型有简单管节点、加强型管节点等。简单管节点是指撑杆间不搭接,不用节点板、隔板或加筋板等加强措施与弦杆连接的节点。简单管节点按受力分为K、T、Y、TK、X型等类型。
管节点处由于外形突变以及弦杆上沿马鞍口各处的刚度不均匀,在外力作用下会引起应力集中。应力集中系数(SCF)指的是弦杆或撑杆上最大主应力值(即热点应力)与撑杆名义应力值之比,即σmax/σn,其中,σmax为热点应力;σn为撑杆上的名义应力。
影响应力集中系数大小的因素包括管节点的类型、热点位置(撑杆或者弦杆、鞍点或者冠点等)、管节点几何尺寸、管节点受力情况。应力集中系数的计算可以参考API RP 2A标准[1]中推荐的Efthymiou公式,或者NORSOK Standard N 004规范。
管节点热点应力幅值(HSSR)等于应力集中系数乘上名义应力幅值。节点对疲劳破坏的承受能力取决于热点应力幅值。
2 断裂力学理论
断裂力学是从力学角度侧面研究宏观的断裂现象的学科,包括宏观裂纹的生成、扩展、失稳开裂等。断裂力学的理论基础是线弹性力学。目前线弹性断裂力学发展较为成熟,工程应用普遍。
线弹性断裂力学的两个重要准则是G准则和K准则,其中G准则为能量准则,K准则为应力强度因子准则。两个准则完全等效,但是实验测定断裂韧度Kc更为方便,所以实际应用中常采用K准则。
对于张开性裂纹,应力强度因子的表达式为[2]
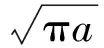
(1)
式中:Y为形状因子;σ为无裂纹的应力;a为裂纹的尺寸。
应力强度因子是表达裂纹尖端应力场强度的重要物理量。应力强度因子的求解主要有复变函数法、积分变化法、应力集中系数法、有限元法、边界元法等。
当裂纹尖端存在小范围屈服时,通过对应力强度因子进行修正,仍然可以采用线弹性断裂力学。对于裂纹尖端存在大范围屈服的情况,线弹性力学不再适用,需要采用弹塑性断裂力学准则。弹塑性断裂力学的准则主要有基于Dugdale(D-M)模型的裂尖张开位移(CTOD)准则以及J积分准则。
CTOD准则表达式为[2]
(2)
式中:δ为裂尖张开位移;E为金属材料弹性模量;σs为屈服强度。
CTOD准则理论依据不够严密,但是应用简单可行,广泛应用于压力容器和焊接结构。
J积分准则的表达式是[2]
(3)
式中:Γ为从裂纹下表面,绕裂纹尖端一周到达上表面的路径;w为应变能密度;T为积分路径边界上的应力矢量;u是积分路径上的位移矢量。
J积分理论依据严格,是描述弹塑性断裂力学裂纹尖端场的重要参数。
Kc,δc,Jc是材料断裂韧度的值,由实验进行测定。当上述理论值K,δ,J超过断裂韧度时,表示结构裂纹失稳扩展。
就目前的研究现状而言,K准则和CTOD准则较为成熟,且求解方法简单,适用于管节点的评估。
3 ECA评估
ECA是以国际认可的实践经验来评估不满足规范要求的结构在特定条件下安全工作的一种评估方法。BS7910规范[3]中对缺陷进行ECA评估采用了失效评定图(FAD)的方法。其具体流程如图1所示。
当材料的韧性很高时,结构的失效模式是由材料特性和力学状态决定的流变破坏,其安全性由结构的极限载荷控制,这时仅采用单个参量(K、CTOD或J)作为制订缺陷评定规范的基础难以适用。因此 Dowling等[4]于 1975 年率先提出了双判据的思想,将载荷也作为一个判据考虑进去,进而在此基础上发展成了综合分析的失效评定图。
FAD提供了一种方便的评价结构由脆断至塑性失稳整个范围的失效风险评定方法。失效评定图的Y轴(断裂比例因子Kr)代表结构对脆性断裂的阻力,而X轴(载荷率因子Lr)代表结构对塑性失稳的阻力。当采用失效评定图对结构进行可靠性评定时,可将评定点(FAP)描于FAD 图上。如果评定点位于由失效评定图的坐标轴和失效评定曲线所构成的区域之内,可认为结构安全;反之,则可能不安全。
BS7910规范是国际通用的金属结构缺陷评估规范。其定义的评定共有3个等级,选用何种级别评定与所选材料、可提供的数据及精确程度有关。
1级,简单评定方法,在已知材料性能数据有限的情况下使用。
2级,常规评定方法。
3级,适用于延性材料,主要是对高硬化指数的材料或需要分析裂纹稳定撕裂断裂时才考虑使用,如奥氏体和铁素体不锈钢。
2级评定是应用最广泛的常规评定级别,适用于导管架管节点。2级评定FAD曲线包括2A级和2B级,2A级利用给出的FAD曲线进行失效评估,不需要应力-应变数据;2B级适用于各种类型的母材和焊缝,需要应力-应变数据,且一般能给出比2A级更精确的结果。
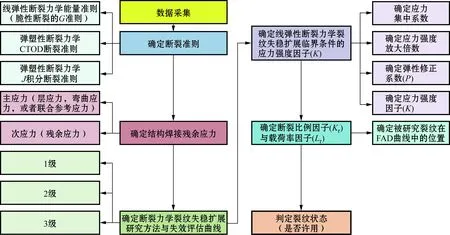
图1 基于FAD的ECA流程图Fig.1 Diagram of ECA based on FAD
下面简单介绍2B级评定方法。典型的2B级FAD评定曲线如图2[3]所示。

图2 2B级FAD曲线Fig.2 Level 2B FAD curve
评定曲线的方程定义如下。
对于,Lr≤Lmax,

(4)
对于Lr>Lmax,

(5)

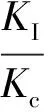
需要注意的是,对于表面缺陷和埋藏缺陷,应力强度因子KI的计算值在裂纹不同部位是不同的。KI的最大值一般发生在最深点(对于表面缺陷)或最靠近表面的点(对于埋藏缺陷)。在两种情况下,参数角θ等于π/2。
应力强度因子表示为[3]
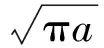
(6)
式中:(Yσ)p和(Yσ)s分别表示主应力和次应力。
计算公式如下[3]:
(Yσ)p=MfwktmMkmMmpm+ktbMkbMb
pb+(km-1)pm,
(7)
(Yσ)s=MmQm+MbQb,
(8)
式中:M为内压膨胀修正因子;fw为截面削弱系数;ktm为膜应力集中系数;Mkm为微观效应膜应力强度因子放大系数;Mm为裂纹参数膜应力强度因子放大系数;pm为主膜应力;ktb为弯曲应力集中系数;Mkb为微观效应弯曲应力强度因子放大系数;Mb为裂纹参数弯曲应力强度因子放大系数;pb为主弯曲应力;km为错位引起的应力放大系数;Qm为次膜应力;Qb为次弯曲应力。
在CTOD准则的评定中,裂纹简单张开位移公式为
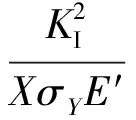
(9)
式中:X值一般在1~2之间,与裂纹尖端情况、几何拘束度及材料的加工硬度有关,近似可采用X=1;E′=E/(1-v2),v为泊松比。
4 裂纹扩展率
断裂力学建立以后,应用线弹性断裂力学的原理提出了多种裂纹扩展计算模型。Paris[5]将疲劳裂纹扩展率与应力强度因子幅值ΔK联系起来,提出了Paris-Erdogan公式(简称Paris公式):
da/dN=A(ΔK)m,
(10)
式中:da为裂纹微扩展;dN是应力循环次数;A和m是与材料、环境和温度相关的常数。
根据裂纹扩展速率da/dN与ΔK之间的关系,疲劳损伤在构件内逐渐积累,达到某一临界值时,形成初始疲劳裂纹,然后初始疲劳裂纹在循环应力及环境的共同作用下逐步扩展,即发生亚临界扩展。当裂纹长度达到其临界裂纹长度时,难以承受外载,裂纹发生快速扩展,以致断裂。
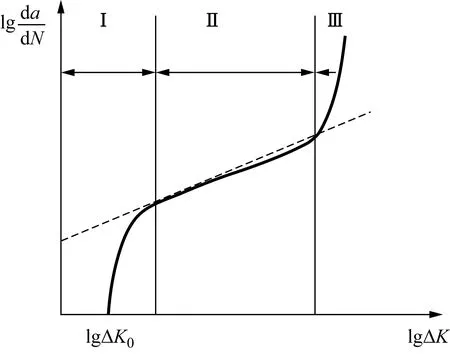
图3 典型的裂纹扩展率曲线Fig.3 Typical crack growth relationship
疲劳裂纹扩展分为三个阶段,如图3所示[2]。当应力强度因子范围低于门槛值时,即ΔK≤ΔK0时,疲劳裂纹基本不扩展,这个阶段为疲劳裂纹的萌生阶段,由于疲劳裂纹萌生后的初始扩展阶段和裂纹的萌生阶段没有明显的界限,因此把裂纹扩展的初始阶段也归入疲劳裂纹扩展的第Ⅰ阶段。第Ⅱ阶段是裂纹的稳定扩展阶段,其应力强度因子范围大于ΔK0。在该区内,裂纹扩展速率da/dN与应力强度因子幅服从Paris公式,也称为Paris区。第Ⅲ阶段是裂纹快速扩展阶段,da/dN很大,疲劳裂纹扩展寿命短,其对裂纹扩展寿命的贡献通常可以不考虑。在工程实际应用中,一般主要以第Ⅱ阶段作为疲劳裂纹扩展寿命的研究区域。
5 管节点的断裂与疲劳评估流程
5.1 评估的数据准备
(1) 裂纹的类型、位置和尺寸,主要来自交流电磁场测量(ACFM)或者其他检验手段;
(2) 管节点及焊缝的外形,来自于设计图纸;
(3) 材料的屈服强度、拉伸强度、应力应变曲线、弹性模量等,来自材料规格书及厂家测试结果;
(4) 载荷及应力,来自导管架整体强度分析、有限元分析等;
(5) 断裂韧度Kc,δc,Jc,来自材料的试验结果,如果没有直接的试验结果值,可以用V型缺口试件冲击功试验估算。
5.2 评估流程
(1) 整体结构分析,提取所关注管节点的名义应力,包括极端风暴工况和疲劳设计工况。
整体结构分析依据HSE、API或者DNV规范,可以采用国际通用的设计软件进行,比如SACS、MOSES、SESEAM等。极端风暴工况的计算载荷需要包含结构自重和上部设施质量、风载荷、海流力和波浪力等。对于结构自振周期在3s以上的,需要进行波浪响应分析。波浪理论采用STREAM波、STOKS V波或者随机波。对于小尺度构件,波浪海流的力采用MORISON公式计算,惯性力和拖曳力系数的取值参考相关规范(HSE、API或者DNV)。
疲劳设计波主要为小振幅波,采用Airy波理论进行波浪响应分析。因为疲劳波工况较多,需要生成传递函数。选取波浪周期1~10 s之间的20~30个值,根据API RP 2A的推荐,波陡采用1/20或者1/25。根据这些波浪工况的结构响应结果来拟合传递函数曲线。疲劳设计工况主要关注波浪引来的应力幅值,因此载荷只需要考虑波浪力。为了求解单个波浪工况(比如周期4 s,波陡1/20)下的应力变化幅值,每个波浪工况分成18个左右的不同相位进行计算,18个应力值中的最大值减去最小值即得到该工况的名义应力变化幅值[1]。
(2) 管节点局部应力分析。
为得到所关注管节点的热点应力及热点应力幅值,上述极端风暴工况和疲劳设计工况的名义应力需要乘上应力集中系数。应力集中系数的获取可以采用有限元分析或者Efthymiou公式进行估算。
热点应力幅值计算公式为[3]
ΔσHS=Δσn.AxKt.Ax+Δσn.IPBKt.IPB+Δσn.OPBKt.OPB,
(11)
式中:Δσn.Ax为轴向名义应力幅;Δσn.IPB为平面内弯曲名义应力幅;Δσn.OPB为平面外弯曲应力幅;Kt.Ax为轴向应力集中系数;Kt.IPB为平面内弯曲应力集中系数;Kt.OPB为平面外弯曲应力集中系数。
热点应力幅根据弯曲度的大小分解成膜应力幅和弯曲应力幅,用于计算应力强度因子幅[6]:
Δσm=(1-Ω)ΔσHSΔσb=ΩΔσHS,
(12)
式中:Δσm为膜应力幅;ΔσHS为热点应力幅;Δσb为弯曲应力幅;Ω为弯曲度。
除了上述的热点应力,还需要根据BS7910规范估算焊接残余应力。
(3) 对极端风暴工况进行断裂评估,并确定裂纹失稳尺寸af。
应力强度因子的求解采用平板模型的Newman-Raju公式结合二维(2D)有限元分析计算[3]。对于表面裂纹,需要分别求解最深点和表面点的应力强度因子。
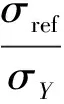
采用塑形应力强度因子准则或者CTOD准则进行2级评定,确定裂纹是否稳定。如果裂纹稳定,继续进行疲劳评估;如果裂纹失稳,评估结束。
(4) 疲劳评估,估算剩余寿命。
裂纹的微扩展用Paris公式进行积分,应力强度因子幅由名义应力幅传递函数、应力集中系数和波谱生成。名义应力幅传递函数中的波陡一般定义为1/20,对于概率表中同一周期而波陡不同的波浪引起的应力值,根据API RP 2A的推荐做法,可以采用与波高成线性比例的方法推算。
疲劳评估既可以用于既有裂纹的管节点扩展寿命的估算,也可用于具有平均缺陷的管节点的寿命估算;对于后者,需要根据检验方法和焊接程序给出一个初始的裂纹微尺寸。微裂纹要考虑位于管节点的鞍点、冠点、鞍点冠点中间以及位于弦杆端和撑杆端等不同位置的情况,共计16个不同的位置[3]。
Paris公式中的A和m的取值,可以参考BS7910 8.2.3.4中关于海水环境下带阴极保护条件的规定值,裂纹增长曲线可以采用简化曲线或者两阶段曲线。
值得注意的是,Paris法则中应力强度因子幅随着裂纹尺寸的变化而变化,裂纹扩展需要进行迭代累加,这点与Miner法则的线性累加原理不同。因此进行疲劳评估时,波浪工况的出现顺序要尽量自然和平均。
6 评估实例
针对图4所示的X型管节点依据BS7910—2005版规范进行2B级评估,计算采用作者开发的JPEFA软件进行。
6.1 材料特性和初始裂纹的数据
材料特性如表1所示。初始裂纹数据如表2、表3所示。

图4 X型管节点的尺寸及裂纹位置Fig.4 X tubular joint sketch and crack location

材料等级断裂韧度CTOD/mm最小屈服强度SMYS/MPa最小拉伸强度SMTS/MPa弹性模量/MPa泊松比材料应变硬化指数V材料应变硬化系数αDH360.153554902060000.3211.3

表2 初始裂纹特征

表3 极端工况管节点应力
6.2 CTOD准则断裂评估
载荷率因子的计算采用局部屈服分析。图5所示FAD图表明评估点位于曲线的左侧,裂纹稳定,可以继续进行疲劳评估。评估结果如表4所示。

图5 断裂评估FAD图Fig.5 Fracture assessment FAD diagram

表4 断裂评估结果
6.3 疲劳评估
波浪概率表和热点应力幅的传递函数共有0°~315°以45°为间隔的8个方向,图6所示为其中一个方向。裂纹增长曲线采用BS7910推荐的简化曲线,海水带阴极保护条件下的计算常数如表5所示。疲劳评估FAD图如图7所示,S-S曲线表示应力应变曲线,R-O拟合是应力应变曲线的近似公式拟合。
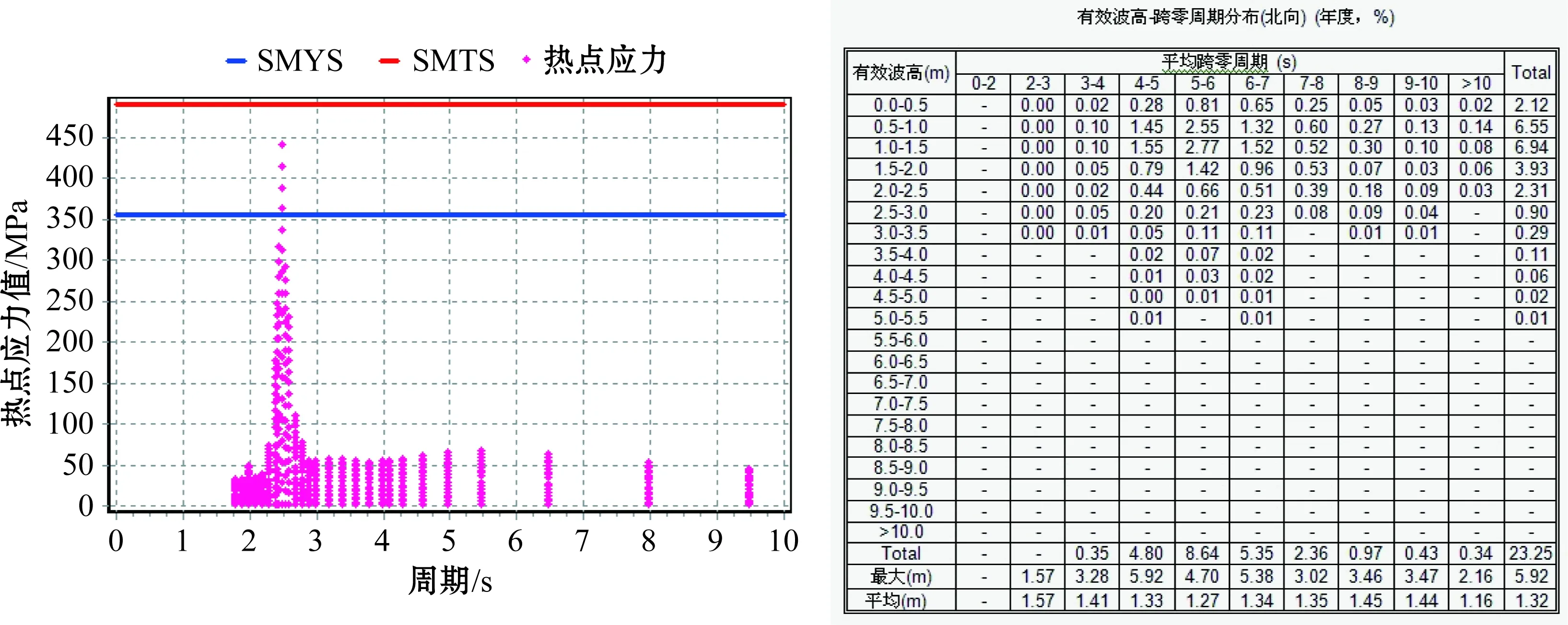
图6 90°方向的热点应力传递函数及波浪概率表Fig.6 Hot spot stress range transfer function and distribution probability of significant wave height for 90° direction
得到的裂纹扩展数据如表6所示。结果表明裂纹扩展的寿命年限为19年。

表5 裂纹增长率常数
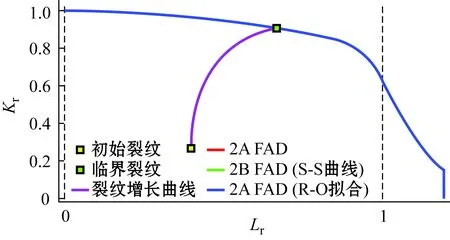
图7 疲劳评估FAD图Fig.7 Fatigue assessment FAD diagram

最终裂纹深度a/mm最终裂纹宽度2c/mm最终断裂比例因子Kr最终载荷率因子Lr裂纹扩展年限/a12.822.40.9040.66719
7 结 论
介绍了一种基于断裂力学的导管架管节点裂纹的断裂评估和疲劳评估方法,并给出了评估实例。在实例评估的过程中,遇到一些细节问题,缺少相应的理论支持。比如对于X型和K型管节点弯曲度Ω的定义,没有明确的文献的支持,目前是参考了T型和Y型管节点的定义方法;又比如疲劳分析中,应力比R的值决定ΔK0的取值,目前R是采用波浪引起的最小应力和最大应力的比值,而没有考虑海流引起的应力,可能存在小的误差;应力强度因子计算中裂纹引起的弯矩释放以及载荷率因子计算中管节点整体屈服分析的应用,是可以采用的挖潜措施,由于需要大量的文献支持,程序没有实现这一点。
随着基础理论的不断进步以及相关研究的日益深入,相信可以尽快解决上述问题。
[1] American Petroleum Institute. API RP 2A—2007. Recommended practice for planning, designing and constructing fixed offshore platforms—working stress design[S]. Washington DC: American Petroleum Institute, 2007.
[2] 程靳,赵树山. 断裂力学[M]. 北京: 科学出版社, 2006.
[3] British Standards Institution. BS7910—2005. Guide to methods for assessing the acceptability of flaws in metallic structures [S]. London: British Standards Institution, 2005.
[4] Dowling A R, Townley C H A. The effect of defects on structural failure: a two-criteria approach[J]. International J Pressure Vessels and Piping, 1975, 3(2): 77.
[5] Paris P C. The Boeing Company Document No. 17867, Addendum N[S]. 1957.
[6] Connolly M P, Hellier A K, Dover W D, et al. A parametric study of the ratio of bending to membrane stress in tubular Y and T joints[J]. International Journal of Fatigue, 1990, 12(1): 3.
FractureAssessmentandFatigueAssessmentofJacketTubularJoints
YIN Yan-kun
(ZhanjiangNanhaiWestOilSurvey&DesignCo.,Ltd.,Zhanjiang,Guangdong524057,China)
The design and assessment of jacket tubular joints are usually performed based on the stress-lifetime (S-N) curve in Chinese ocean oil and gas engineering projects, while the fracture mechanics methods are rarely employed. This article describes the basic theory of fracture mechanics, ECA, fatigue crack growth law and general assessment procedure, and then gives an assessment example by JPEFA program.
ocean oil and gas engineering; tubular joint; fatigue assessment; fracture mechanics; ECA
TE54
A
2095-7297(2014)02-0129-07
2014-05-29
尹彦坤(1980-),男,工程师,主要从事海洋石油固定式平台结构设计方面的研究。
