牙轮钻机回转减速机构机械系统仿真及有限元分析

项丹

(太原重工油膜轴承分公司,山西太原 030024)

牙轮钻机回转减速机构机械系统仿真及有限元分析

项丹

(太原重工油膜轴承分公司,山西太原 030024)

建立牙轮钻机回转减速机构的三维传动模型,利用Adamas对该减速机构进行了机械系统仿真,通过定义机构之间运动关系,得出各齿轮转速和初始接触力的关系曲线。在此基础之上,对受力大的齿轮对在Ansys-Workbench环境下进行有限元分析,得出齿轮的应力分布云图,从而对设计进行评估,以及为接下来的优化设计提供数据支持。

Adamas 有限元分析 接触 齿轮 仿真

1 引言

回转减速器是牙轮钻机回转机构的核心部件，其性能的好坏直接影响牙轮钻机的工作状况。牙轮钻机回转减速机构的组成由图1所示。电机通过输入传动轴(轴3)将扭矩和转速传递给齿轮18，通过该二级圆柱齿轮减速器，将回转机构所需要的转速通过输出传动轴(轴1)传递给钻杆。

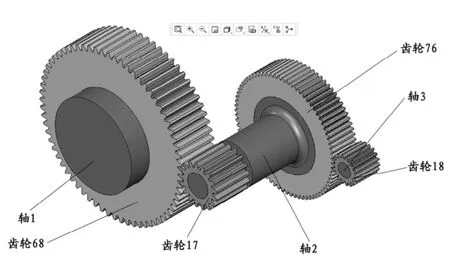
图1 回转减速机构组成

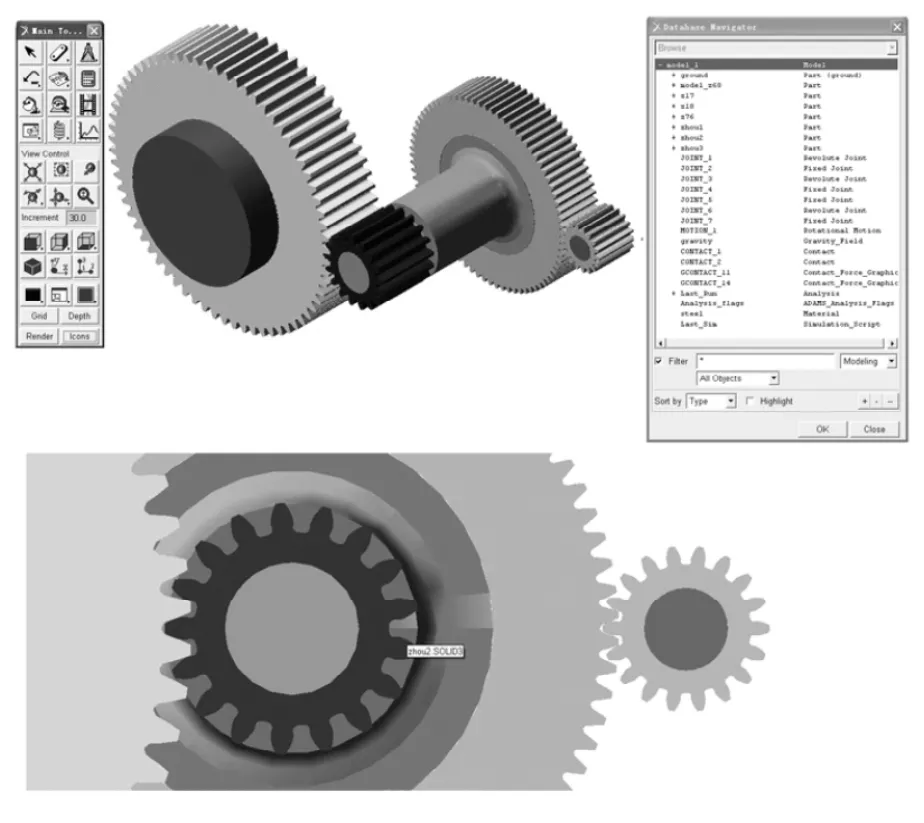
图2 减速机构虚拟样机模型

2 减速机构的机械系统仿真(MSS)

机械系统仿真在虚拟样机试验中有着重要作用[1]。在Adams中通过使用刚体、运动副和施加载荷来构建机械系统的虚拟样机[2]。

图2为牙轮钻机减速机构的虚拟样机模型，在该模型中，轴1、轴2和轴3施加相对于地基的旋转副，齿轮18和轴3固定为一体、齿轮76、齿轮17和轴2固定为一体、齿轮68和轴1固定为一体。定义完约束之后为了能使各齿轮副之间传递运动和动力，需要在啮合的齿轮之间添加接触。接触的计算采用冲击函数法，通过定义接触刚度系数使啮合齿轮间不发生渗透[3]。

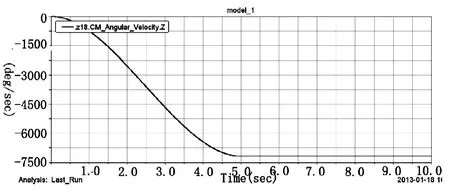
图3 齿轮18角速度时间曲线

图4 齿轮17角速度时间曲线

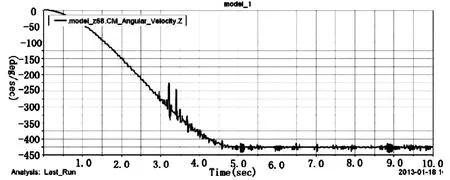
图5 齿轮68角速度时间曲线

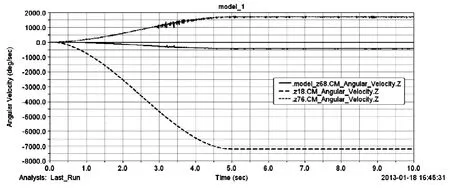
图6 各齿轮角速度对比曲线

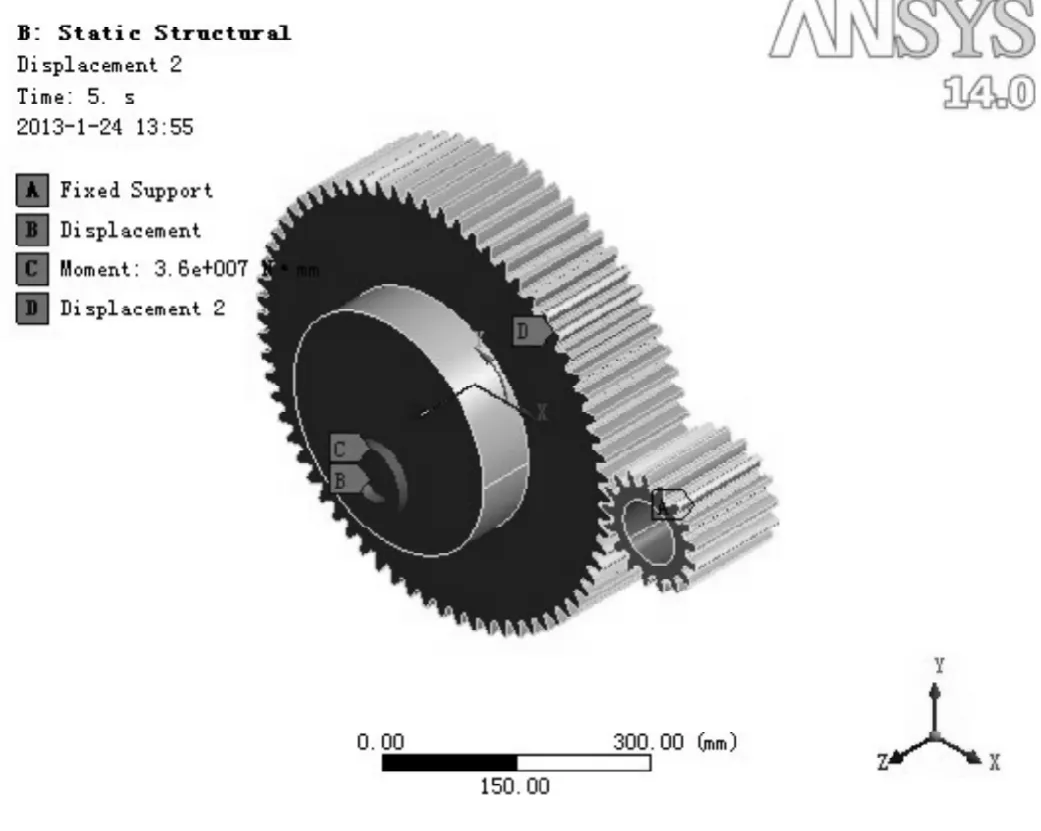
图7 有限元分析前处理

图8 分析计算收敛曲线

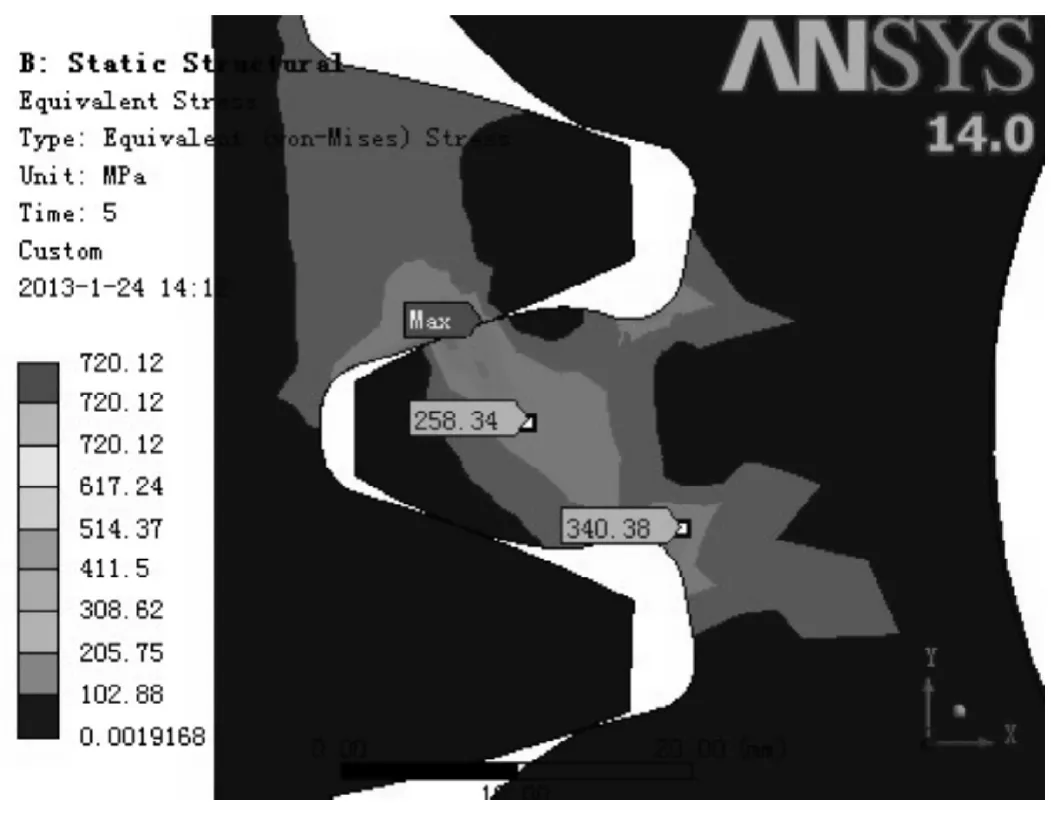
图9 齿轮等效应力云图

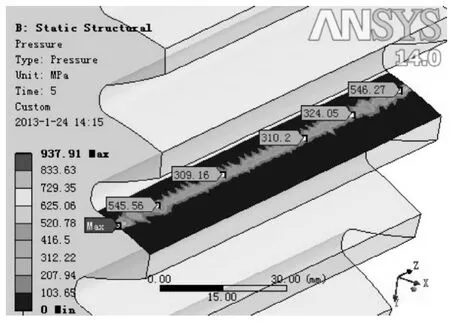
图10 齿轮接触应力云图

定义好各约束之后，在轴3上施加旋转驱动，旋转驱动的类型是角速度(deg/s)。仿真的角速度是根据实际情况来定义的。轴3输入电机的转速为1500r/min，因此在仿真的0-5s内，轴3的角速度从0增加到7200deg/s。5s-10s轴3保持7200deg/s的转速，将仿真的步长设置为1000。

图3为仿真完成之后齿轮18的角速度随时间的变化曲线。从图中可以看出齿轮18经历了加速和匀速两个阶段的运动状态，从图中可以看出齿轮18运行平稳。

图4为齿轮17的角速度-时间关系曲线，从曲线中可以看出齿轮17在运动过程中存在微小的角速度波动，利用齿轮副的接触仿真可以查看仿真中齿轮运行的速度波动，更加的符合实际情况。

图5为齿轮68的角速度时间关系曲线，从图中可以看出齿轮68在仿真中也存在着速度的波动。

图6为齿轮18、齿轮72(齿轮17)和齿轮68角速度的对比曲线，从图中可以看出各曲线的角速度符合齿轮传动比的计算公式。从仿真中也可以看出，齿轮的运行比较平稳，满足实际要求。

3 齿轮接触分析前处理

在实际运行当中，由于各齿轮的转速存在差异，受力最大的齿轮为齿轮68，因此有必要校核齿轮能否满足强度的要求，利用Ansys-Workbench进行计算。

齿轮的强度计算属于接触分析，从一般的物理意义上讲接触的表面包含有以下特性。

(1)两表面之间不会发生相互渗透；

(2)可传递法向压缩力和切向的摩擦力[4][5]。

接触是状态改变的非线性，系统的刚度取决于接触状态。在接触的计算方法上采用的是增强的拉格朗日公式，该方法是基于罚函数方程：

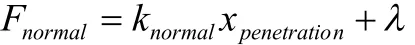
从公式中可以看出对于一个有限的接触力 Fnormal对应于一个接触刚度 knormal，接触刚度越高，穿透量 xpenetrantion就越小。理想状态下对于无穷大的 knormal可以实现零穿透。但是对于增强的拉格朗日公式，在数值计算中是无法实现的，但是只要能够满足 xpenetrantion足够小，就能保证有精确的计算结果。增强的拉格朗日公式由于还增加了额外因子，使计算对于接触刚度 knormal值变得不敏感，使计算更加容易收敛。

在前处理中，定义两对接触，分别为轴1-齿轮68定义的接触类型为绑定接触(bond)，在绑定接触中，不允许面或线间有相对滑动或分离。可以将此区域看做被连接在一起。因为接触长度/面积是保持不变的，所以这种接触可以用作线性求解。齿轮68-齿轮17定义的接触类型为有摩擦接触(Frictional)，这种情况下，在发生相对滑动前，两接触面可以通过接触区域传递一定数量的剪应力。模型在滑动发生前定义一个等效的剪应力，作为接触压力的一部分。一旦剪应力超过此值，两面将发生相对滑动。该情况只适用于面接触，在这里摩擦系数定义为0．08。

前处理的方式如图7所示，为了使接触能够实现，将轴1留有一个沿着Z轴的旋转自由度，因此需要建立一个局部坐标系，坐标系的类型设置为圆柱坐标系，将轴1的两端面施加位移约束，两端面可以沿着Z轴转动并且在这两个端面上施加扭矩。对于齿轮68同样采取该约束方式，约束区域为齿轮68的两端面。齿轮17的边界条件为固定齿轮17两圆柱面。

4 齿轮接触分析结果

运行有限元分析计算，计算完成后，从受力曲线图8中可以看出，经过多次迭代之后，计算结果得到收敛。

图9为齿轮的等效应力(von-Mises)云图，从图中可以看出齿轮最大的应力为720MPa，齿轮材料的屈服极限为800MPa，强度最大的地方发生在齿轮接触处，一般来说塑性材料许用挤压应力为屈服强度的2-2．5倍，因此齿轮设计满足强度要求。

图10为齿轮68和齿轮接触区域的应力分布，从图中可知最大的接触应力为937MPa，齿轮材料的许用接触应力为1600MPa，齿轮满足接触强度的要求。

5 结语

(1)通过机械系统仿真和有限元分析计算可以得知设计的减速机构模型运行当中的受力变化和应力分布状况，可以为设计提供理论依据[6]。

(2)有限元分析中轴在扭矩作用下所受应力不大，可以做相应的优化设计，减小轴的直径从而节约成本。

(3)在齿轮的有限元分析中可以采用平面应力分析，从而简化模型，达到节省计算时间的目的。

[1]徐德民.惩罚函数法在接触分析中的应用[J].中华钢结构,2007,08:12-15.

[2]David Rhodes. Do FEA Tools Give The Same Answers[M].United States of America,2011:200-230.

[3]石磊.Pro/E结构分析实例和工程应用[M].北京:科学技术出版社,2010:1-50.

[4]浦广益.ANSYS workbench12基础教程与实例详解[M].北京:中国水利水电出版社,2010:21-35.

[5]Vince Adams.Assembly modeling in Pro/MECHANICA:Getting stared in Pro/Enfineer[J].Pro/E:The Magazine,December,1998,6:Pp.36 to 37.

[6]濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2006:198-199.

Established the model of the blast-hole drill's rotation deceleration institutions,utilized the Adams to simulation this deceleration institutions.By defining the motion relationship among the parts,obtaining the curves of angular velocity changes with time.And make the finite element analysis to the gear pair which bearing the largest force in ansys- workbench environment.obtaining the von-mises stress of gear pair distribution which can evaluate design,And the provide data support to optimization design of the next step.

Adamas;finite?element?analysis;contact gear simulation

项丹(1982-),女,满族,辽宁铁岭人,工程师,主要从事油膜轴承的设计。