基于一级倒立摆模型仿人机器人控制算法研究*

胡 静 ，姜大伟 ，王华振 ，姚 禹 ，谭海东

（1.长春工业大学 软件职业技术学院，吉林 长春 130012；2.长春工业大学 机电工程学院，吉林 长春 130012）

0 引言

仿人机器人是机器人研究领域中的一个重要分支，仿人机器人的步态行走系统是在以往深入研究仿人行走系统的各项技术环节，以提高仿人机器人行走环节的拟人化程度，使其各项功能最大程度地接近人类运动，从而保证仿人机器人在不同环境下完成任务的能力的基础上提出的，是步行机器人研究中的一个重要而又关键的技术。但是仿人机器人的步态行走系统是一个多变量、非线性、强耦合的复杂动力学系统，要实现和提高机器人的行走性能，必须研究实用而有效的步态控制方法，实现机器人的实时稳定步行[1-2]。很多学者采用较少的变量来获得仿人机器人的步态行走轨迹，将倒立摆模型应用于机器人步态规划中，取得满意的控制效果[3-5]。

本文在深入研究倒立摆模型基础上，应用PID控制算法对仿人行走系统进行控制，并在开发以STM32+CPLD为核心19轴集成运动控制平台中进行验证，通过对比理论与原理样机实验数值，关节输出最大相对误差为2.25%，表明了该控制方法的准确性和有效性。

1 仿人机器人行走问题描述

设计的10自由度仿人行走系统的机构模型如图1所示。

采用左右腿对称的结构方式。以右腿为例，其自由度分配为：髋关节2个自由度，膝关节1个自由度，踝关节2个自由度。主要结构参数：大腿长度：214 mm；小腿长度：214 mm；脚部长度：55 mm；大腿质量：6.5 kg；小腿质量：3.5 kg；脚部质量：2.5 kg。仿人行走系统的运动过程为：上位机下达控制指令给驱动电机；驱动电机通过同步齿形带驱动各关节转动，从而实现仿人行走系统的步行运动。各关节输出范围如表1所示。驱动电机主要参数如表2所示，驱动电机输出端安装减速比为1:50的减速器，提高了电机的最大力矩值。

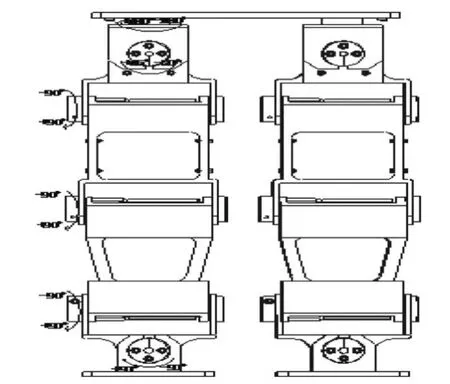
图1 10自由度仿人行走系统的机构模型

表1 仿人行走系统各关节输出范围

表2 57号步进电机技术参数

2 基于倒立摆模型的仿人机器人数学模型的建立

和人类步行相似，仿人机器人的步态行走是机器人的重心由支撑腿向前运动，摆动腿由支撑腿的后方摆到支撑腿的前方，两条腿的交换在瞬间完成的。在这样的行走过程中，将仿人机器人行走系统简化为一个倒立摆模型[6]，如图 2所示。

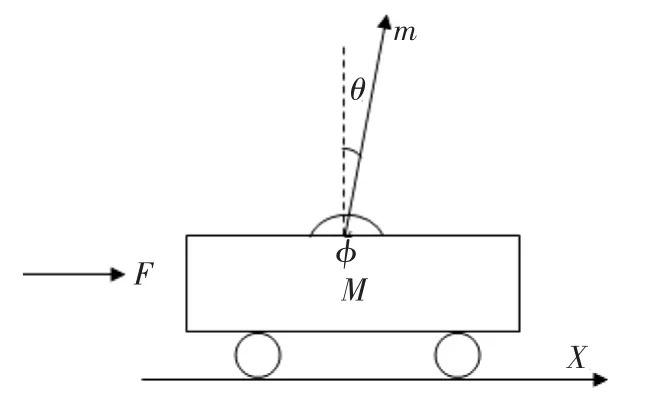
图2 倒立摆模型

质量为m的小球固结于长度为L的细杆（可忽略杆的质量）上，细杆又和质量为M的小车铰接相连。通过控制施加在小车上的力F（包括大小和方向）能够使细杆处于θ＝0的稳定倒立状态。在忽略其他零件的质量以及各种摩擦和阻尼的条件下，推导小车倒立摆系统的数学模型。设细杆摆沿顺时针方向转动为正方向，水平向右方向为水平方向上的正方向。当细杆摆顺时针往右运动时水平方向施加的力应该为水平向右。

现对小车和细杆摆分别进行隔离受力分析：

对小车有：

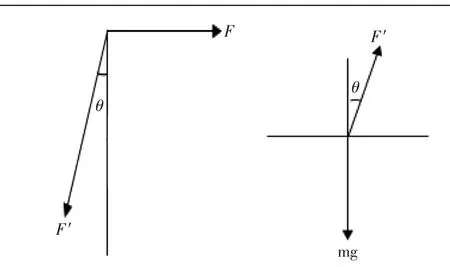
图3 小车和小球的受力分析图

对小球水平方向受力为：

式中 s=x+l sinθ。 由式(1)、(2)得：

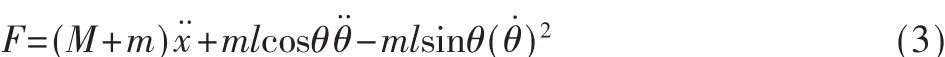
小球垂直方向受力为：

由式(3)、式(4)得：

故可得以下运动方程组：

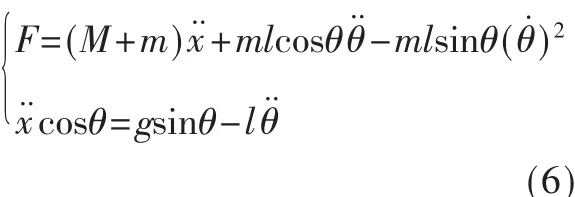
以上方程组为非线性方程组，故需做如下线性化处理：

下面进行系统状态空间方程的求解：以摆角 θ、角速度θ˙、小车位移 x、加速度x¨为系统状态变量，Y为输出，F为输入。

由线性化后运动方程组得：

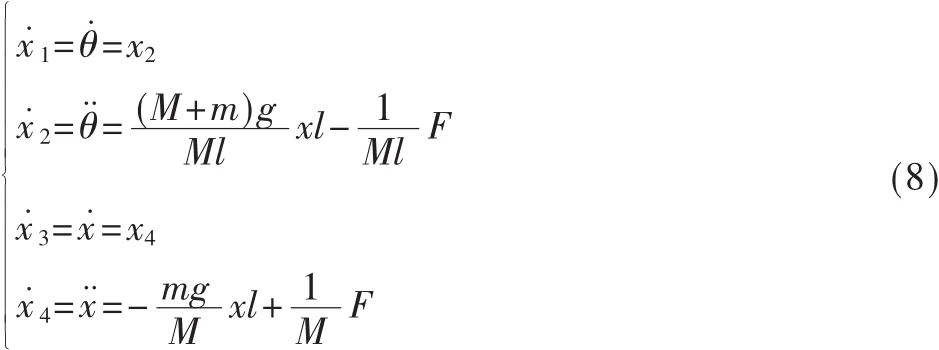
故空间状态方程如下：

用MATLAB将状态方程转化成传递函数，取M=2 kg，m=0.1 kg，l=0.5 m代入，可以得出角度对力 F的传递函数为：

位移X对外力F的传递函数为：

3 仿人机器人步态行走控制器的设计

3.1 PID控制器的设计

由上节对倒立摆模型的描述，仿人机器人的步态行走要求它的姿态角达到一个期望值，当仿人机器人受到干扰离开期望值时，如果姿态角不能及时恢复，仿人机器人姿态失衡，最终会导致机器人行走失败。为了使仿人机器人姿态角稳定在期望值，保持仿人机器人姿态平衡，实现仿人机器人稳定行走的目的，本文采用以仿人机器人姿态角和位移实现双闭环的PID控制算法[7-8]，干预姿态角和位移的变化，使其始终保持在稳定状态，从而实现仿人机器人的稳定步态行走。

PID控制器是一种线性控制器，它将给定值r(t)与实际输出值 c(r)的偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量，对控制对象进行控制。是一种应用较为广泛的控制算法，其控制性能优越，结构简单，方便调节[9]。PID调节器各校正环节的主要作用有：

(1)比例环节：偏差一旦产生，调节器立即产生控制作用以减小偏差即时成比例地反应控制系统的偏差信号e(t)。

(2)积分环节：主要用于消除静差，积分作用的强弱取决于积分时间常数，进提高系统的无差度。

(3)微分环节：能反应偏差信号的变化趋势(变化速率)，相当于引入一个有效的早期修正信号，从而加快系统的动作速度，减小调节时间。

首先，建立PID控制器的微分方程为：

式中，e(t)=r(t)-c(t)。

再得到PID控制器的传递函数为：

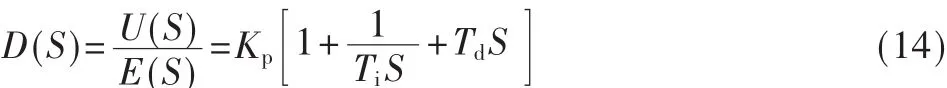
3.2 PID控制器参数调节

在MATLAB/Simulink中建立仿人机器人模型，同时采用试凑法对PID参数进行调节[10]。首先，建立没校正之前的θ-F单闭环控制系统，由于未加进控制环节，故系统输出极易发散。给系统加入PID控制环节，如图4所示。

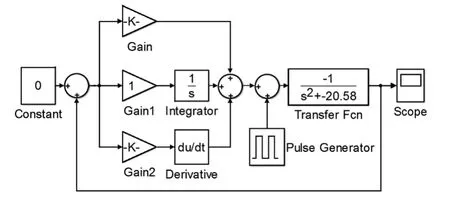
图4 θ-F单闭环控制系统框图

设置系统稳定值为0，给系统一个初始干扰冲击信号，采用试凑法不断调整PID参数，当系统在时域内达到稳定后，进行离散化分析，建立离散模型系统控制框图如图5所示。

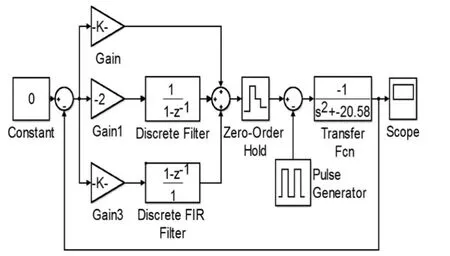
图5 离散模型系统控制框图

如图6所示，经调节后，当 Kp=-110，Ti=-4，Td=-1 500，系统响应稳定，超调＜0.3%，调节时间＜0.2 s。至此，离散域的控制参数调节顺利实现。图7为建立的仿人机器人双闭环控制系统。

图6 控制系统响应曲线图

4 仿人机器人步态实验

4.1 仿人行走系统控制系统硬件

仿人机器人运动控制器在增加了CPLD芯片后，控制系统如图8所示。实验目的是验证本文所提PID控制器的合理性及准确性，该仿人机器人下肢有10个自由度，上肢有9个自由度，以STM32+CPLD为核心的控制系统总体方案，单一的关节控制可以使用一个51单片机芯片最小控制系统，控制步进电机运动[11]。

图7 位移-角度控制系统框图

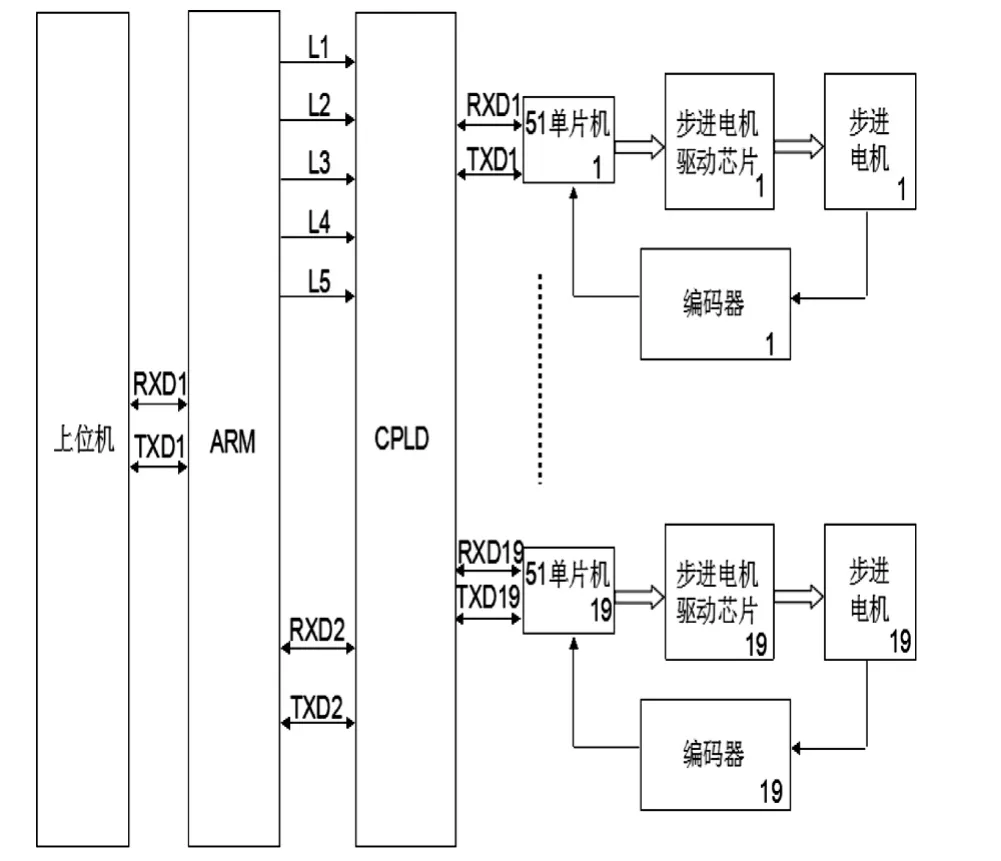
图8 19自由度控制系统简图

4.2 数值对比结果分析

调节行走系统原理样机末端执行器位姿为给定位姿gs3T3(θ)。通过编码器和倾角传感器测得行走系统各关节输出。比较数据值，如表 3所示。

通过验证数值对比结果得出，关节输出最大相对误差为2.25%，表明了本文采用仿人机器人步态行走系统PID控制算法的正确性及高精确度。

5 结论

本文针对仿人机器人步态行走不稳定的问题，以倒立摆为控制对象，建立仿人机器人步态行走数学模型。在建立数学模型时，首先用牛顿—欧拉方法建立数学模型，而后用动态系统空间状态方程法导出状态方程系数矩阵，然后用MATLAB对数学模型进行从状态空间到传递函数的变换（包括传递函数的拉氏变换与Z变换），得到系统的传递函数模型。最后建立仿人机器人姿态角和位移的双闭环控制系统，采用PID控制算法对仿人机器人姿态角和位移进行调节。系统响应稳定，超调量＜0.3%，调节时间＜0.2 s，得到满意的控制效果。以19自由度仿人机器人进行实验验证，其关节的输出相对误差最大为2.25%，可实现仿人机器人稳定的步态行走，表明了本文采用仿人机器人步态行走系统PID控制算法的正确性及高精确度。

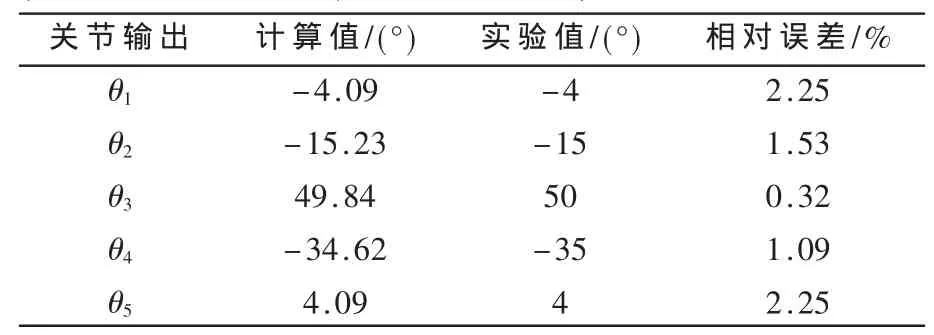
表3 右腿各关节输出的计算值与实验值比较

[1]毕盛，闵华清，陈强.仿人机器人步态规划反馈控制研究综述[J].计算机工程与应用，2011(7)：30-33.

[2]付根平，杨宜民，李静.仿人机器人的步行控制方法综述及展望[J].机床与液压，2011(23)：154-159.

[3]Tang Zhe，ER M J.Humanoid 3D gait generationbased on inverted pendulum model[C].22nd IEEE International Symposium on Intelligent Control Part of IEEE Multi-conference on Systems and Control，2007.

[4]毕盛，闵华清，陈强，等.一种仿人机器人斜坡运动步态规划方法[J].华南理工大学学报(自然科学版)，2010(11)：148-154，160.

[5]李龙澍，王唯翔，王凡.基于三维线性倒立摆的双足机器人步态规划[J].计算机技术与发展，2011(6)：66-69.

[6]黎君，阎世梁.一级倒立摆模糊 PID控制器设计[J].国外电子测量技术，2012(4)：50-52.

[7]郭宏，吴海洋，巫佩军.基于变系数 PID的无刷直流电动机双闭环系统[J].北京航空航天大学学报，2012(1)：1-5.

[8]王启源，阮晓钢.独轮自平衡机器人双闭环非线性PID控制[J].控制与决策，2012(4)：593-597.

[9]刘慧博，王静，吴彦合.无刷直流电机模糊自适应 PID控制研究与仿真[J].控制工程，2014(4)：583-587.

[10]张斌，姚有峰.基于串行总线下最小控制系统实现方式的研究[J].现代电子技术，2009(11)：149-151.

[11]袁安富，徐金琦，王伟，等.基于双 STM32多旋翼无人机控制系统设计[J].电子技术应用，2013，39(11)：136-138.