CFI中基于动态区域划分的非平稳杂波抑制方法*

熊秀娟，肖 磊，陈 波，彭 勇，王耀彬

(西南科技大学 计算机科学与技术学院，四川 绵阳 621010)

0 引言

在临床医学领域中，CFI能够实时准确无创地探测血流速度，是诊断心血管疾病的重要技术[1]。在CFI中，探头接收到的回波信号包括血流信号、杂波信号（由血管搏动和组织慢速移动引起），通常杂波信号强度比血流信号强度高出 40～80 dB[2]，这给准确地估计血流速度带来了极大困难。因此，为了得到真实可靠的血流速度，必须对回波信号中的杂波进行充分地抑制。

目前常用的杂波抑制器有：低阶FIR滤波器[3]、基于投影初始化的IIR滤波器[4]和回归滤波器[5]。其中低阶FIR滤波器、投影初始化IIR滤波器和回归滤波器均属于静态滤波器，它们的通带截止频率、阻带衰减等特性较为固定。当杂波信号是平稳信号时，这些滤波器能够获得较为理想的效果。但在实际临床诊断中，由于人体呼吸、脉搏等因素造成组织加速运动，导致杂波信号属于非平稳随机信号，静态滤波器对此类信号的处理效果不理想。后来有学者提出非平稳杂波抑制法[1]，该方法对杂波抑制效果较好，但是在杂波信号较弱的区域会造成误消除，导致血管内血流信息的损失，对血流速度的估计造成极大误差。

本文在非平稳杂波抑制法的基础上提出一种基于动态区域划分的非平稳杂波抑制方法。该方法首先利用能量特性对回波信号进行动态区域划分，然后结合非平稳杂波抑制法和多项式回归法对不同区域的信号分别进行处理。实验结果表明，该方法的算法复杂度低，满足超声诊断设备的实时性要求；同时，该算法能较好地抑制杂波并保证流速度剖面的完整性，是一种快速有效的杂波抑制方法。

1 原理与方法

1.1 动态区域划分和局部平滑

多普勒回波信号是在同一探测位置发射K次脉冲波得到的一维向量矩阵。将轴向采样容积为M的K个复解调信号排成二维矩阵，则对回波信号处理的过程即是对二维矩阵进行运算。其中，信号构成如图1所示。通常，信号矩阵的行向量被称为慢时信号，列向量被称为快时信号[2]。

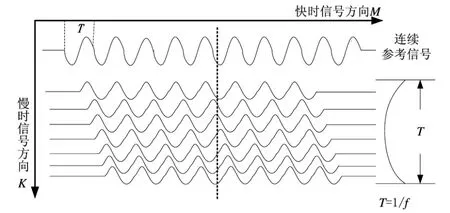
图1 信号构成图

复解调回波信号可表示为矩阵X：

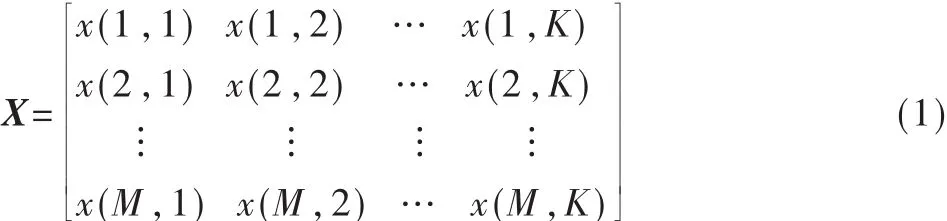
其中K是慢时信号方向的采样容积(脉冲重复数)，M是快时信号方向的采样容积。

回波信号慢时信号方向的平均能量E_X表示为：

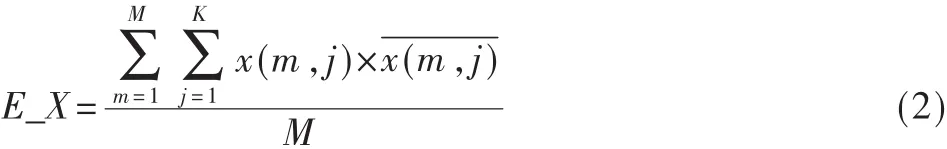
同理，快时信号方向上不同深度的慢时信号能量E_Xs(m)可由式(3)表示：

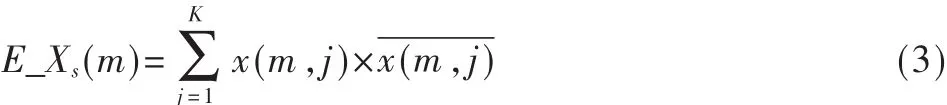
其中j是慢时信号方向上的第j个采样点，m是快时信号方向上的第m个采样点。由于不同区域的组织产生的回波信号强度不同，以式(4)的方式对信号进行划分，可以区分不同组织区的信号。

通常在动态组织区，杂波信号的强度比血流信号强度高出 40～80 dB，因此可以由式(5)再次对动态组织区的信号进行划分：

其中E_M是动态组织区快时信号上慢时方向的平均能量。

静态组织区远离血管，整体趋于静止，所以回波信号趋于平稳，且不携带任何速度信息；血流区分布在血管内部，加之血管中的血流速度呈抛物线分布且相对较稳定，因此血流区的信号相对平稳；杂波区受呼吸、脉搏等影响，造成血管及血管附近组织具有加速度，因此杂波区信号属于非平稳信号。

为保证杂波滤波器自适应于组织运动且不造成血流信息的损失，本文算法采用空间平滑法处理动态组织区，如式(6)：

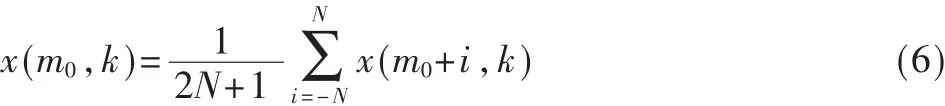
其中N是快时信号方向上参与空间平滑的区间半径。

1.2 杂波频率估计[1]

复解调回波信号x(m，k)用复指数形式表示为：

x(m，k)=A(m，k)ejφ(m，k)(7)其中 A(m，k)是信号的幅值，φ(m，k)是信号的相位。通常在多普勒回波信号中，杂波信号的相位可以用一个低阶多项式表示：

由此可见，对杂波信号的瞬时频率进行估计，就是求出多项式系数ad的过程。

引入矩阵R和向量φ，对拟合多项式(9)求解得多项式系数向量a：

又由式(9)可得杂波瞬时频率矩阵W=[w(m，1)w(m，2)… w(m，K)]T的表达式：

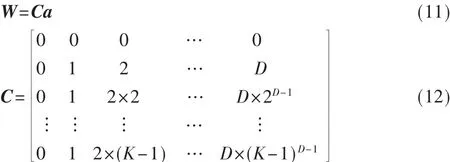
将式(10)得到的系数向量a带入式(11)就可以进一步求得杂波的瞬时频率矩阵W。对于D的取值，参考文献[5]通过分析低阶多项式拟合的原理并进行大量的实验后得出：当D≤4时，多项式能够有效地拟合低频信号。在超声彩色血流成像中，当D=3时，拟合多项式能够精确地描述杂波的瞬时频率。

1.3 局部非平稳杂波抑制

多普勒回波信号经过动态区域划分和杂波瞬时频率估计后就可进行混频处理。其中混频是为了将非平稳杂波信号的频率搬移到零频附近。为保证血流信号点的完整性，本文算法只对杂波区信号进行混频处理。利用前文得到的杂波瞬时频率，混频信号可表示为：

混频过程可用式(14)表示：

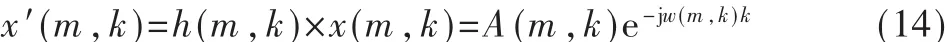
通过混频处理，杂波信号的非平稳性大大降低，此时通过常用的静态滤波器就可以对杂波信号进行充分抑制。由于血流区信号可能含有较弱的杂波，因此本文算法选用能够避免数据点损失的多项式回归滤波器对杂波信号进行抑制，这样既保证了杂波信号的有效去除，又保证了血流信息的完整性。算法流程如图2所示。

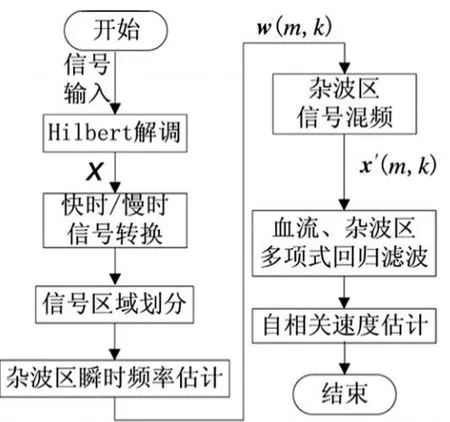
图2 算法流程图

2 仿真实验

2.1 仿真模型与参数

为了分析和验证所提出的杂波抑制方法的有效性，本文在计算机上用MATLAB R2012a软件平台进行仿真，运行环境为 Centrino2（1.66 GHz），采用丹麦技术大学学者Jenson等研制的Field ii软件包仿真超声多普勒回波信号。仿真所用的超声血流模型如图3所示，仿真参数如表1所述。图4是通过仿真模型得到的一条回波信号波形图。

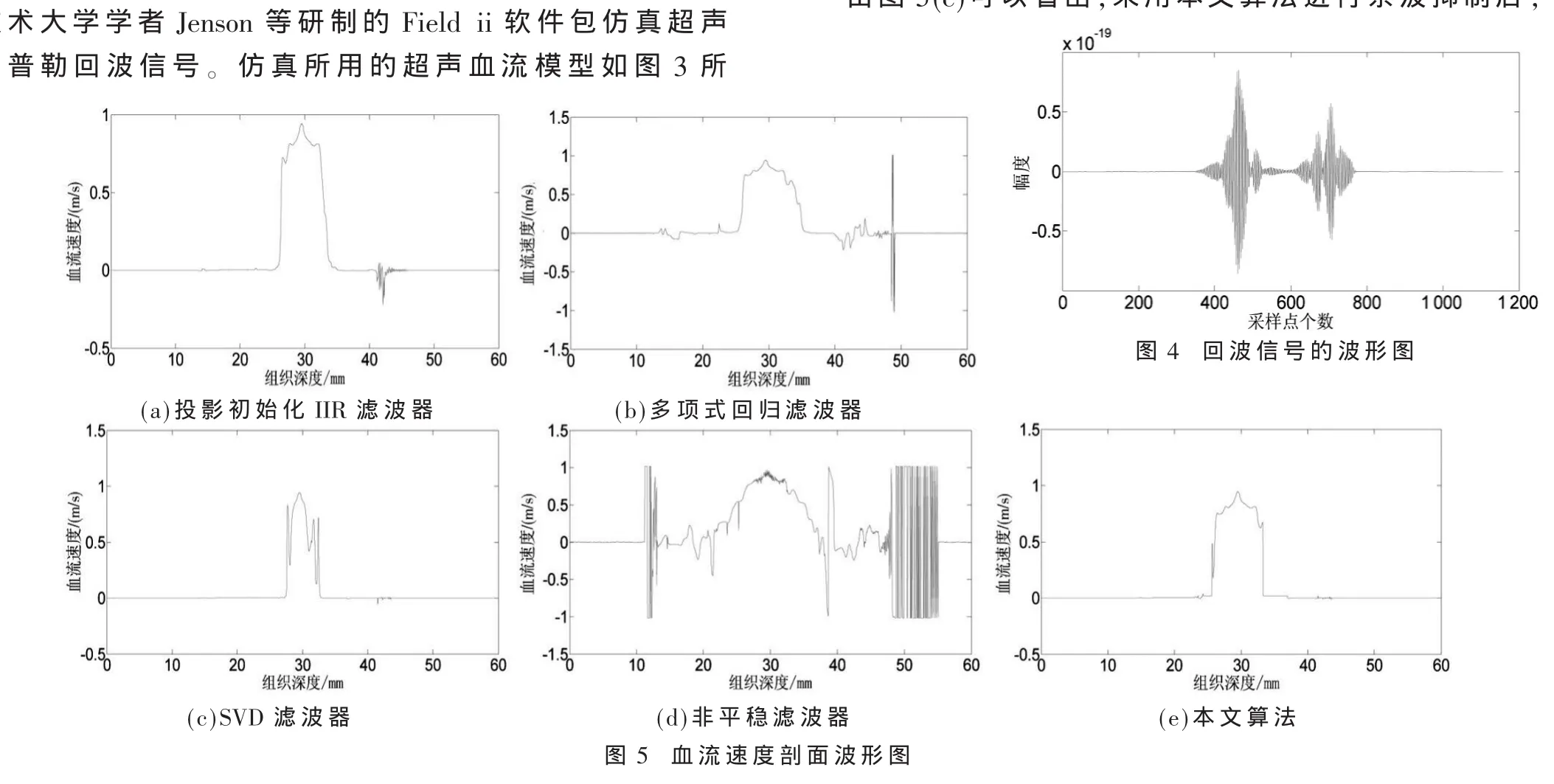
2.2 仿真实验结果

为验证本文算法对杂波的抑制效果，将其与投影初始化滤波器、多项式回归滤波器、SVD滤波器和非平稳滤波器进行比较。图5所示的是一组（16条）回波信号经过各滤波器后自相关估计得到的相应的血流速度剖面波形图，图6所示的是218组相邻回波信号通过各滤波器后自相关估计、编码映射得到的血流速度图。两图直观地展示了不同滤波器对杂波的抑制性能。

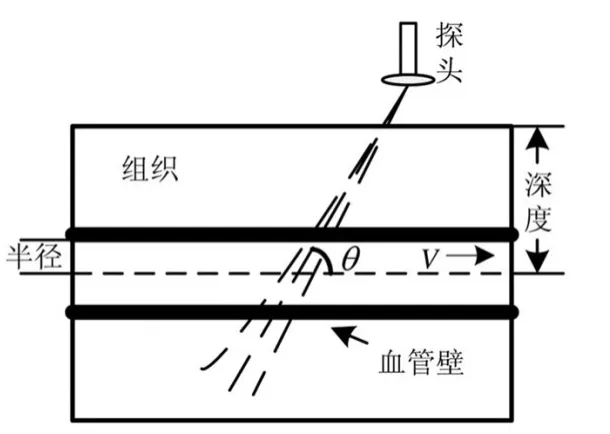
图3 超声血流模型图

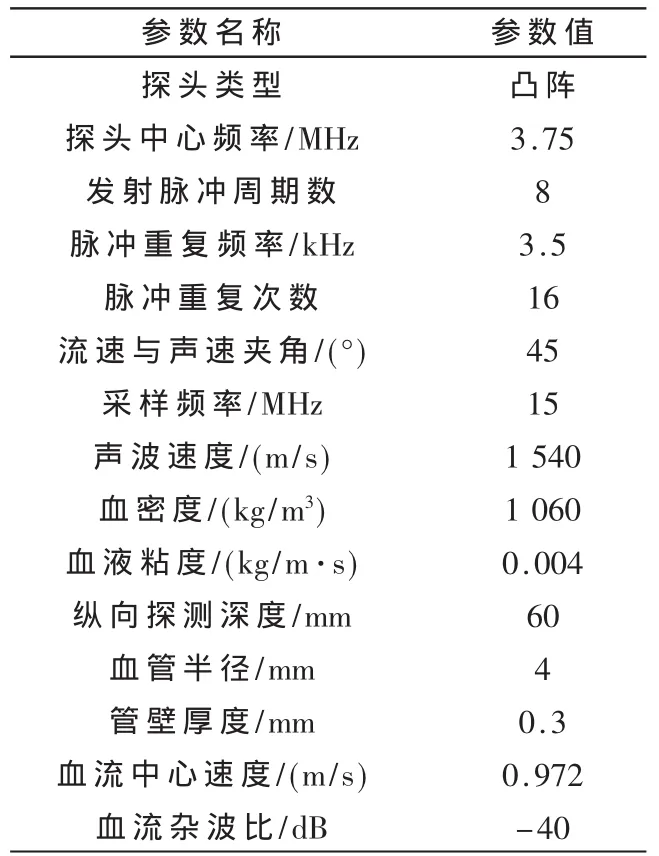
表1 Field II仿真参数设置

图6 编码映射血流图

由图5(e)可以看出，采用本文算法进行杂波抑制后，自相关估计得出的血流速度信息几乎仅存在于血管内部（约在扫描深度24 mm～34 mm之间，血管理论直径为8 mm），且速度分布相对比较完整，这与实际情况基本相符。由图5(a)～5(d)可以看出，经过其他滤波器处理后的回波信号经自相关估计后得到的血流速度信息不仅存在于血管内部，也存在于组织区，这显然与实际情况不符。

从图6(e)可以看出，本文算法得到的血管壁清晰、完整，血管截面速度分布均匀；从图 6(b)和 6(d)可以看出，经过回归滤波器和非平稳滤波器得到的血流速度分布不均匀，且组织区出现伪血流信息；从图6(c)中可以看出，经过SVD滤波器后得到的血流速度分布不完整，血管内速度出现零点，且血管直径明显小于理论值，成像效果较差；从图6(a)可以看出，投影初始化IIR滤波器由于采用固定频率作为截止频率而造成数据点损失较大，使得血管直径明显小于理论值（理论血管直径为8 mm）。

此外，为了从客观上对本文算法进行评价，文章从最大速度估计、杂波血流比和算法运行时间三方面对算法进行比较。比较结果如表2所示。

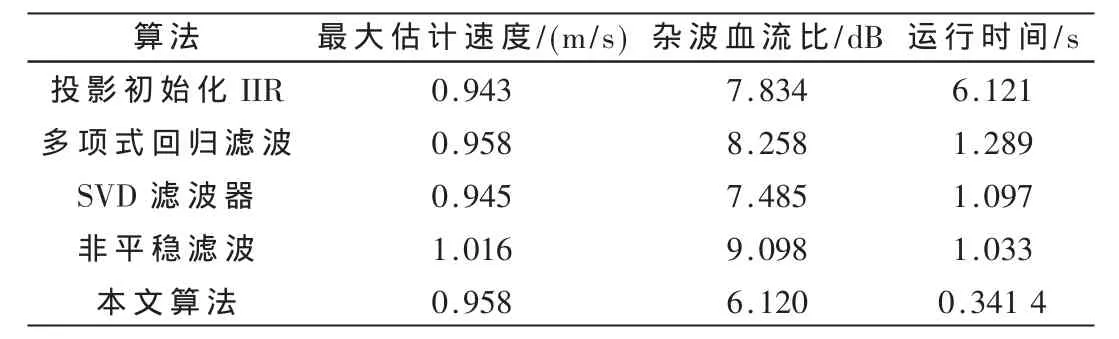
表2 算法比较表

从表2中可以看出，本文算法估计的最大速度值接近理论最大速度值0.972 m/s(本文算法的最大估计速度与多项式回归滤波器相同，这是因为该算法采用多项式回归法对血管中心区域信号进行处理)，表明采用本文算法对杂波信号进行抑制时，原始信号中的血流信号损失较小；经本文算法滤波后，信号的杂波血流比明显低于其他几种滤波算法，这表明该算法能够有效地对原始信号中所含的杂波信号进行抑制；在运行时间上，本文算法的运行时间远小于其他几种算法，这是由于该算法对静态组织区的信号不做处理导致的。综上所述，本文算法在杂波抑制效果、血流信息的保留和算法时间复杂度上都能取得较为满意的结果，由此证明此算法较其他杂波抑制算法更有效。

3 结论

本文提出的基于动态区域划分的非平稳杂波抑制方法一改以往采用单一滤波方法进行杂波抑制的模式，通过分析回波信号的特点，首先采用动态区域划分法将信号分割为不同部分，再根据各部分信号的特点做出相应处理。本文算法采取对静态组织区信号完全保留的方法，既保证滤波器不会在此区域引入噪声，又保证了运行速度。同时，对杂波区和血流区采取不同的滤波方法，既保证了杂波的有效去除，又避免了血流信号的损失。此外，该算法采用矩阵进行推理运算，易于工程实现。

另外，杂波瞬时频率的估计是基于低阶多项式来实现的，当多项式阶数取值适当时，能较好地描述杂波频率，但当阶数取值欠佳时，不能很好地对频率进行描述。因此，采取一种能精确描述杂波瞬时频率的方法将是下一步研究的目标。

[1]王沛东，沈毅，王艳.超声彩色血流成像中非平稳杂波的抑制[J].中国生物医学工程学报，2008，27(2)：240-243.

[2]尤伟，汪源源.超声彩色血流成像中基于动态区域划分抑制杂波的方法[J].仪器仪表学报，2010，31(3)：594-599.

[3]JENSEN JA.Estimation of blood velocities using ultrasound[C].Cambridge，UK：Cambridge University Press，1999：195-226.

[4]CHORNOBOY E S.Initialization for improved IIR filter performance[J].IEEE Trans.Signal Processing，1992，40(5)：543-550.

[5]PARK G，KIM Y，SHIM H，et al.New adaptive clutter rejection based on spectral decomposition and tissue acceleration for ultrasound color Doppler imaging[C].IEEE Joint UFFC，EFTF and PFM Symposium，2013：1484-1487.