一种适用于射频数字功放的量化策略*

陈剑斌，朱 蕾，周 强，陈昆和

（解放军总参谋部第六十三研究所，江苏 南京 210007）

0 引言

随着当前通信系统集成度的不断提高，功放高效率、低功耗的要求显得越来越重要。传统模拟功放为了保证放大信号的线性性能，必须工作在线性区域，这大大限制了其效率性能。而基于△∑调制器(DSM)的数字功放[1]通过将数字信号转换为脉冲信号，驱动晶体管工作在饱和开关状态，能够大大提升功放的效率。数字功放结构图如图1所示。

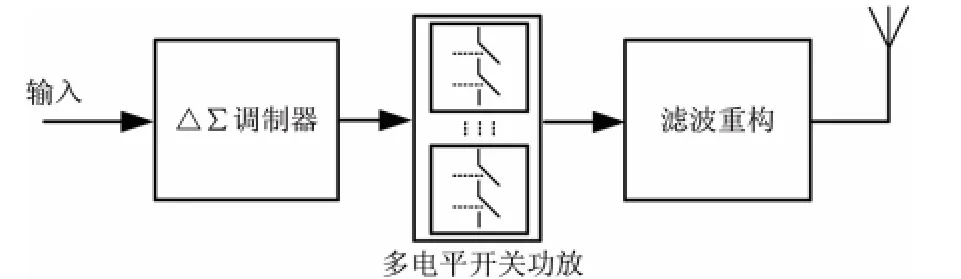
图1 数字功放结构图

通过开关工作，数字功放理论上能够获得100%的效率。但在实际电路中，当前端DSM的输出驱动电平发生跃变时，开关功放会消耗一定能量对电路中的电容进行充放电，从而影响数字功放的效率[2]。为了降低数字功放的切换损耗从而提升高频场合下的功放效率，需要尽量减少DSM输出的切换频率。本文利用电力电子系统中的滞环比较控制思路，结合DSM结构提出了一种新的量化策略。该策略下DSM量化器通过记忆前一时刻的量化输出，实时更新当前的量化门限值，从而在不改变DSM硬件结构的前提下有效降低DSM输出的切换速率。

1 DSM量化策略

图2所示为DSM的原理框图[3]。

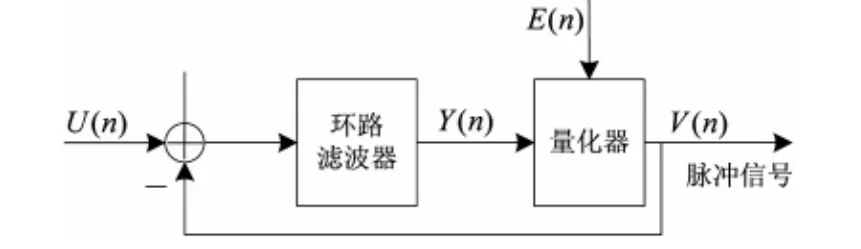
图2 DSM结构示意图

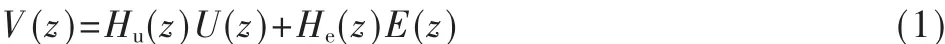
其中，Hu(z)为信号传递函数，He(z)为噪声传递函数。根据DSM的结构，减少DSM输出切换频率的一个直接方法是降低过采样率。降低过采样率时，为了保证带内SNR性能，需要相应地提高DSM阶数。但无论是降低过采样率还是提高DSM阶数，都会改变DSM的环路滤波器结构。为了在不改变DSM硬件结构的前提下实现对输出切换频率的控制，考虑改进量化器的量化策略。现有的DSM结构中，量化器采用固定门限量化策略。对于单比特量化情况：

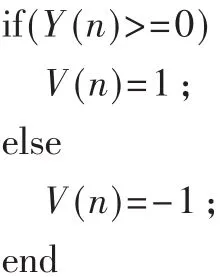
1.1 单比特DSM的可变门限量化策略

在电力电子系统中，为了解决比较器输入接近门限值时出现“振铃”现象，往往采用滞环比较器[4-5]，其基本特征是比较器采用不同的正、反向比较电压。借鉴滞环比较思路，提出一种可变门限的DSM量化策略：

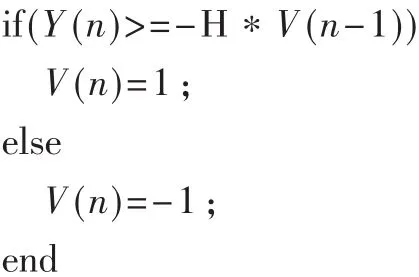
其中迟滞指数H＞0。在可变门限量化策略下，量化门限由固定值变为与前一时刻量化输出相关的值。假如前一时刻量化输出为1(-1)，则当前时刻量化器输入值必须小于-H(大于H)其输出才会发生改变。相比固定门限量化策略，可变门限策略下量化器输入需要变化更大的值才能最终引起输出发生变化。因此采用可变门限策略可以降低DSM输出的切换频率。

图3为单比特量化示意图，阴影部分代表量化误差。固定门限量化策略下，量化器前一时刻输出为1时，量化误差面积为：

可变门限量化策略下对应的量化误差面积为：

注意到对称性，相比固定门限，可变门限量化策略下量化误差的总面积增加：

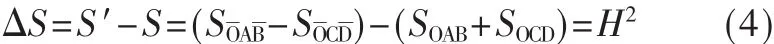
公式(4)表明，相比固定门限量化，可变门限量化策略下DSM输出在切换频率减小的同时SNR性能会有一定程度的下降。

1.2 多比特DSM的可变门限量化策略

进一步根据公式(2)可以概括电平量化下可变门限策略的量化方案为：

假设固定门限量化策略下量化门限值为QL=[Q1，Q2，…，Qn，…，QN-1](-1＜Qn＜1，1≤n≤N-1)。 则在可变门限策略下，若前一时刻的输出为 V(n-1)＞Qn，则当前时刻下的量化门限变化为：Q′L=(Q1-H，Q2-H， …，Qn-H，…，QN-1+H)。

容易验证，当 N=2时，上述的量化方案与式(2)一致。

如图4所示，对于固定门限量化策略，2 bit DSM的量化门限为[-2/3，0，2/3]。而在可变门限策略下，根据前一时刻的量化输出，多电平DSM门限值实时地进行更新。与单比特情况类似，容易推出2 bit可变门限策略下量化误差总面积增加量为3H2。

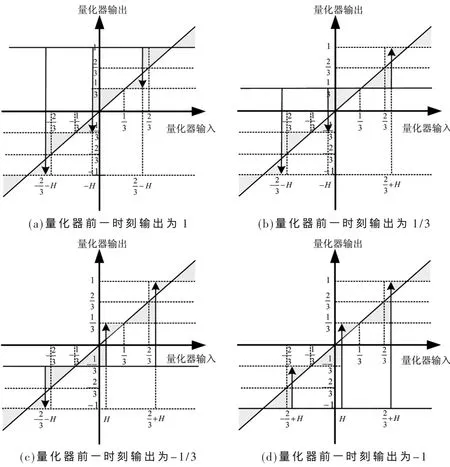
图4 可变门限量化示意图(2 bit输出)

2 仿真结果

前面通过理论定性分析了可变门限策略下DSM输出序列的切换频率及其SNR变化情况，下面进行仿真验证。不失一般性，这边考虑基于CRFB结构的4阶带通DSM[6]，输入为35 MHz单音信号，系统采样频率为400 MHz。

2.1 迟滞指数范围

为了保证DSM调制器的稳定性，首先分析不同输入幅度下允许的最大迟滞指数。

图5所示为DSM处于稳定和失稳时的输出序列频谱。比较两种情况，可以看到失稳时DSM序列频谱的带内噪声成型已经不可见，并且带外的信号谐波和杂散幅度迅速增大。因此以DSM输出序列频谱的带内SNR指标作为稳定性判据，以分析不同输入幅度下允许的最大迟滞指数。

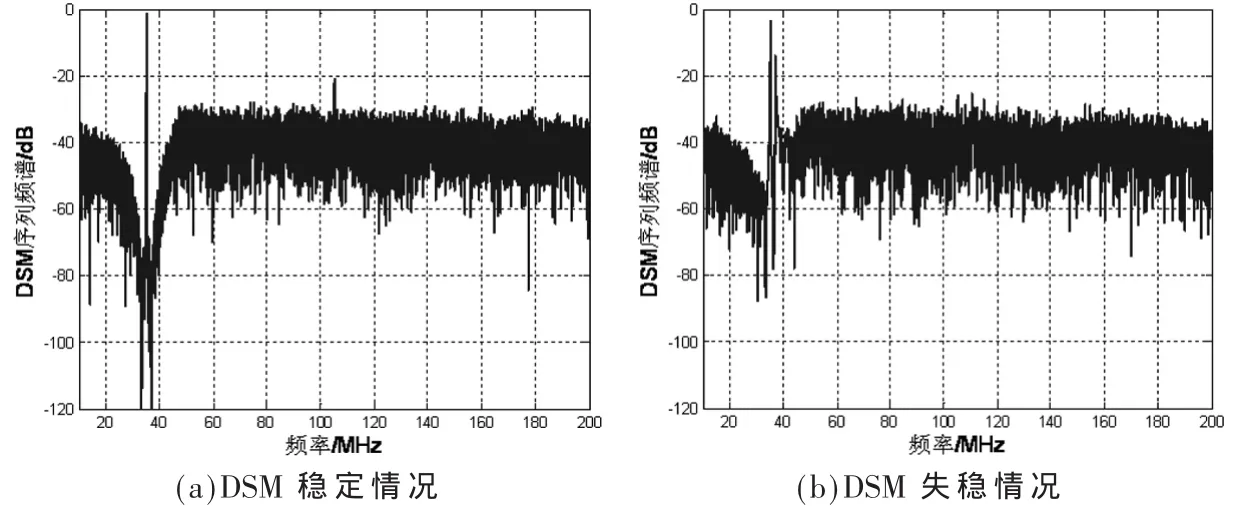
图5 稳定与失稳条件下的DSM输出

分析图 6仿真结果：在固定 H_inf下，输入单音信号幅度增加，系统的稳定性下降，对应此时量化器允许的最大迟滞指数整体上呈现下降趋势；另一方面，H_inf取值越小，对应 DSM结构越稳定。因此相同输入幅度下，H_inf越小，量化器允许的迟滞指数越大。与H_inf类似，量化电平数越多DSM的稳定性越好[3]。因此2 bit量化下的最大稳定迟滞指数整体上要大于单比特量化。

2.2 平均切换频率性能

下面在系统稳定前提下仿真分析DSM输出序列的切换频率指标。根据参考文献[2]，定义平均切换频率fav：

其中，fs为系统采样频率；N为序列时钟周期数；Ntr为高低电平间的切换次数，反映脉冲序列中的脉冲总数。仿真中迟滞指数取为[0，0.2，0.4，0.6]。

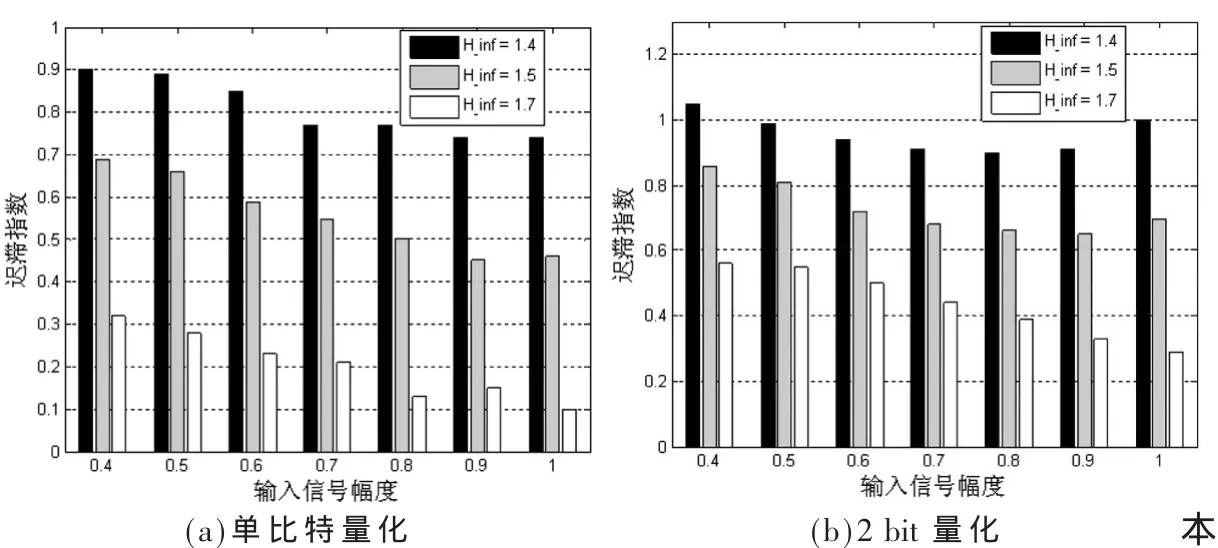
图6 输入幅度与最大稳定迟滞指数关系

不同迟滞指数下的fav比较如图7所示。迟滞指数越大，则量化器输入需要变化更大的值才能最终引起输出发生变化，对应DSM输出序列的fav越小。注意到2 bit量化情况下，当迟滞指数为0.6、幅度为0.4时，此时DSM输出序列的fav反而增大。这是由于DSM实质是一个负反馈系统，当信号幅度较小且迟滞指数较大时，相比2 bit固定门限量化策略，可变门限策略下量化器由于迟滞作用输出电平在±1/3之外还将引入±1，从而使得此时DSM输出序列的fav增加。

2.3 带内信噪比性能

根据前面分析，迟滞指数越大，量化误差也越大。因此随着迟滞指数增大，DSM输出序列的带内SNR逐渐下降，仿真结果如图8所示。根据表1、2的定量分析结果，相比固定门限策略，当H=0.2时，单比特和2 bit量化下fav分别减少23.7%和19.7%，此时带内信噪比分别只下降了1.8 dB和3.6 dB；当 H为 0.6时，单比特和2 bit量化下带内信噪比分别下降了11.6 dB和 8.3 dB，此时 fav分别减少 52.9%和 34.5%。

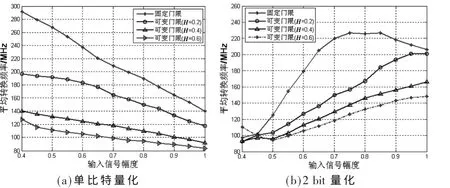
图7 不同迟滞指数下的f av比较

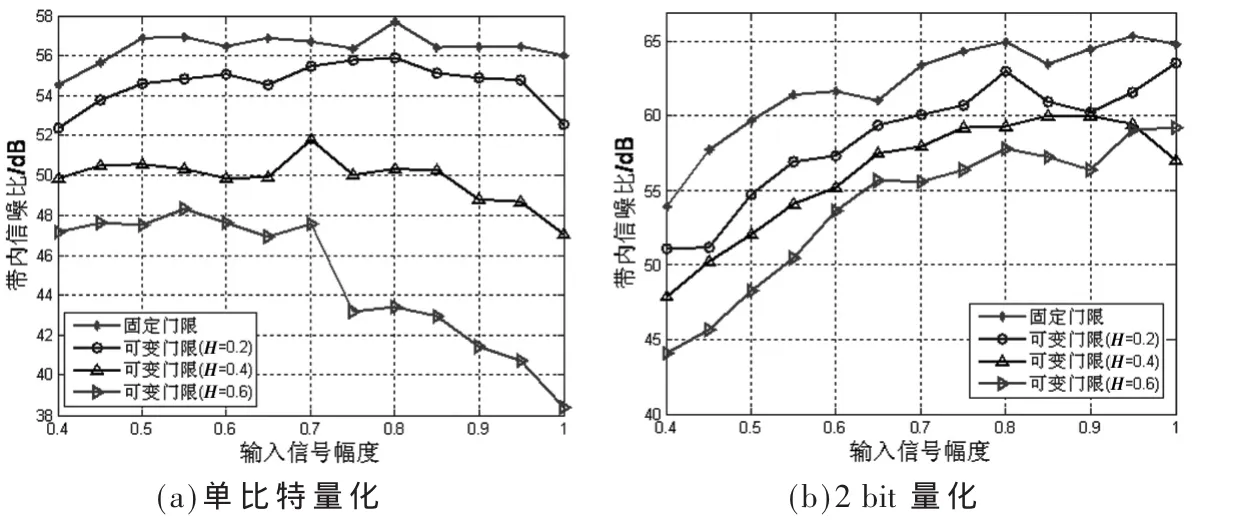
图8 不同迟滞指数下的SNR比较

表1 不同迟滞指标下的平均转换频率 (MHz)

表2 不同迟滞指标下的平均带内信噪比 (dB)

3 结论

本文利用滞环比较控制思路，在DSM调制器中提出了一种可变门限的量化策略，并通过理论和仿真分析了该策略下DSM输出序列的平均切换速率fav以及带内SNR性能。结果表明，相比固定门限量化策略，可变门限量化策略通过设置合适的迟滞指数，在带内SNR性能下降有限的情况下能够显著的降低DSM输出序列的平均切换频率。因此，基于本策略的DSM调制器可以有效减少高频应用场合下数字功放的切换损耗，从而提升功放整体效率。另一方面，考虑到本文策略下DSM输出序列平均切换频率降低是以牺牲一定的带内SNR性能为代价，考虑利用遗传算法[7]、文化算法[8]等进化策略优化迟滞指数H，从而在fav与SNR之间获得一个最优平衡是下步工作的方向。

[1]朱蕾，周强，谭笑.基于多比特带通△∑调制器的射频数字功放[J].电子技术应用，2013，39(8)：102-105.

[2]JOHNSON T，STAPLETON S.RF Class-D amplification with bandpass sigma-delta modulator drive signals[J].IEEE Tran.on Circuits and System，2006，53(12)：2507-2519.

[3]SCHREIER R，TEMES G C.Delta sigma数据转换器[M].北京：科学出版社，2007.

[4]程瑜华，邝小飞，孙玲玲.采用迟滞比较器的自激振荡功率放大器行为特性分析[J].电路与系统学报，2012，17(6)：100-107.

[5]彭彦豪，张为，刘洋.一种应用于锁相环频率合成器的自动选带电路[J].微电子学，2011，41(4)：498-501.

[6]刘冠东.基于∑△技术的调制器的设计与验证[D].长沙：湖南大学，2011.

[7]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，2002.

[8]杜琼，周一届.新的进化算法——文化算法[J].计算机科学，2005，32(9)：142-144.