混合动力电驱动系统的模糊控制策略研究*
2014-12-10鲁子卉
鲁子卉
(长春职业技术学院 工程技术分院,吉林 长春 130033)
混合动力电驱动系统HEDS(Hybrid Electric Driving System)采用高性能电动机作为动力部件,同时配有电能存储单元与燃油作为系统的能源供给,具有较高的系统功率密度和灵活的控制性能。通过合理利用多种能量源的技术优势,可以实现较单一能量源系统更高的工作效率。HEDS是目前工程机械、车辆、航空等领域中大功率驱动系统的重要设计方案之一,尤其是随着近年来控制技术、总线通信技术和电力电子技术的迅速发展,HEDS系统的应用日益广泛[1-4]。由于采用了多种能量源协同工作,系统控制算法是HEDS研发过程中的重要环节[5]。控制算法的研究对于提高HEDS控制效果、动态性能和工作效率等都具有重要意义[6-7]。
本文首先采用有限状态机理论针对HEDS进行建模与分析,进而基于多变量模糊控制对控制算法进行设计,提取关键控制规则进行优化,最后通过Matlab系统仿真,对所提出的控制方案进行了仿真验证。
1 HEDS系统建模
一个典型的HEDS由发动机、耦合器、电动机、逆变器、动力电池组等组成。电动机作为系统中的机械功率输出装置,通过逆变器来连接直流母线,电机控制器实时地通过变频控制来调节电动机输出功率、发动机燃烧燃油,以此带动小型永磁同步发电机发电,与电池共同组成混合动力能量源,为电动机提供电能供应。为了对HEDS进行数学描述,系统根据不同的控制决策在不同的工作模式之间进行实时切换。
为了对控制算法进行研究,需要对每种动力部件的数学模型进行进一步的详细描述。动力电池组是一个复杂的非线性时变系统,为了避免模型过于复杂,忽略温度和使用寿命对电池特性的影响,采用简化的内阻等效模型,将电池组视为一个包含可变内阻的电压源,电池组的输出为端电压与端电流。发动机建模采用稳态实验数据加一阶延迟修正的双PI控制模型,其中,第一个PI控制环表示发动机的输出功率调节,控制器根据系统需求功率和发动机实际功率调整发动机目标工作转速;第二个PI控制环为发动机的力矩控制,控制器根据发动机目标转速与实际转速之差控制发动机的工作力矩,发动机与电池组的数学模型如式(1)~式(4)所示。


其中,Te为发动机力矩,Tm为电机力矩,f为延迟函数,τ为时间常数,∂t为传动效率,is为电机传动比,Tr为发动机负载力矩,Pre为需求功率,Pe为发动机实际输出功率,χne为发动机转速控制信号,ζTe为发动机转速控制信号,fPI与 λPI为 PI控制函数,Ubat和 Ibat分别为动力电池组的端电压与输出电流,Rn为内阻,Vbat为电池组开路电压,ξbc为电池组的库伦效率,Pbat为电池组输出功率。
考虑到模型的动态特性,电池组的开路电压Vbat与内阻Rn都是与电池组当前的电荷状态SoC(State of Charge)有关的变量,SoC采用电流积分算法法进行估计:

其中,Q为电池组初始容量,Qmax为电池组最大容量,Kυ为电池衰老对SoC影响的修正系数。
2 模糊控制算法
基于上述模型对控制策略进行设计与优化,HEDS控制的核心问题在于使整个系统实现工作效率需求的同时协调控制多个工作单元,从而使效率达到最优。工作效率分两个层次:(1)单个工作单元自身的效率最优,例如早期的发动机自身效率达到最优曲线控制算法等,这一类控制思路虽然简单有效,但个体的最优不等于整体的最优;(2)通过个体单元之间的协同控制,实现整体的最优,即基于系统优化的控制策略。为了实现上述系统效率最优控制,同时使系统可以体现出良好的工作效果,必须通过模糊控制算法来实现HEDS的逻辑控制。模糊逻辑结构采用2输入1输出的T-S型结构,首先将电池SoC与负载功率作为模糊输入进行模糊化处理,进而输入到T-S模糊控制器中,模糊输出为发动机的目标功率,通过模糊规则来决定系统的模糊输出,输入与输出的隶属度函数如图1所示。解模糊的过程采用重心法,模糊运算采用Zadeh算法,如式(6)所示。

其中,J与Q表示隶属度函数,x表示触发隶属度规则的模糊变量。
仿真过程采用美国US06工况作为速度运行工况,结合上述模糊隶属度函数设计HEDS模糊控制规则。系统中电动机的输出功率由综合控制器根据驾驶员踏板信号决定,因此模糊控制算法主要解决了电动机的功率在发动机发电机组与电池组之间的合理分配。模糊规则的主要设计思路是在满足系统功率需求的前提下,负载功率越高则发动机输出功率也越高;负载功率越低则越倾向于发动机不输出功率。当电池组SoC越低时发动机输出功率越高;电池组SoC越高时,则发动机输出功率越低。列举部分模糊规则如下:

图1 Mandani模糊控制隶属度函数

其中,K1,K2,…Kn为n条模糊控制规则的输出系数:
上述模糊控制规则反应了输入与输出的模糊逻辑对应关系,在建立的过程中依靠模拟人工智能来体现混合动力系统的设计经验。显然这样的控制算法虽然具有智能性,但却无法实现效率的最优,因此有必要对模糊算法进行进一步的优化。通常对模糊的优化主要分为两种,一种是对隶属度函数进行优化,另一种是对模糊规则进行优化,本文采用第二种思路,即对模糊规则进行优化。每条模糊规则中均含有一个待定系数Ki,Ki的选取对于发动机发电机组与电池组的功率分配起着直接作用。对模糊控制算法建立优化模型,因为每一个Ki对应着每一条模糊决策下的发动机输出功率,通过查表最优曲线则可以得到不同的发动机效率。因此可以将系统效率写成关于Ki的函数,同时将优化目标函数定为系统效率的倒数,即可以得到优化目标函数的表达式如式为:

约束条件为:

其中,SoC_Low与SoC_High为电池组SoC的下限与上限,Pe_max为发动机最大功率,Pm为电动机功率,Pm_max与Pm_min为电动机峰值功率与最低功率,ξm、ξe与 ξbat为电动机效率、发动机效率与电池组效率。
3 Matlab仿真分析
为了对所提出的模糊控制策略及其优化方法的正确性和有效性进行验证,对建立的模型及速度工况在Matlab中进行系统仿真,仿真过程采用固定步长0.01 s。仿真结果如图2所示。可以看出电池组的输出电流始终控制在-100 A~+200 A区域内的电池组效率较高,同时较低的电池充放电电流有助于提高电池使用寿命。仿真结果同时表明,发动机功率在低功率时处于关闭状态,当发动机开启时则大部分时间处于中高功率区间,避免了低功率工作状态,有助于控制降低发动机排放。

图2 HEDS系统仿真结果
在整个仿真工况中随机抽取18个观测点,与未优化前的系统效率进行对比,结果如图3所示。可以看出,未优化前平均效率为75.8%,经过优化后系统效率有了明显提高,平均效率达到 81.4%,提高了 5.6%,表明所设计的模糊控制算法及其优化方法合理有效。
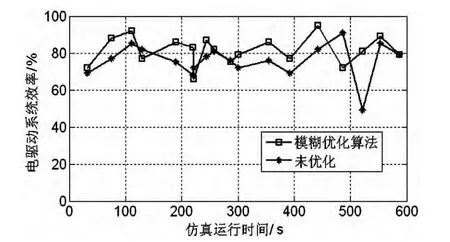
图3 电驱动系统效率仿真结果
本文建立了混合动力电驱动系统的数学模型,并基于该模型进一步提出了多变量模糊控制算法,进而对模糊规则进行了优化。Matlab仿真表明所设计的模糊控制算法使混合动力系统实现了良好的控制效果,工作效率有明显改善,优化之后的混合动力电驱动系统效率较优化之前提高了5.6%。
[1]MONHEY H,SHARK L K.System optimization of the electric delivery cars using PSO algorithm[J].Asian Journal of Control,2008,44(1):108-114.
[2]JOHANNES S,EMADI M.Optimal control of parallel hybrid vehicles based on PSO algorithm[J].Asian Journal of Control,2010,8(13):24-29.
[3]陈清泉,孙逢春.混合电动车辆基础[M].北京:北京理工大学出版社,2001.
[4]杨大柱.Matlab环境下FIR滤波器的设计与仿真[J].电子技术应用,2006,32(9):101-103.
[5]ZHANG M Y,YANG Y,MI C C.Analytical approach for the power management of blend-mode plug-in hybrid electric vehicle[J].IEEE Transactions on Vehicular Technology.2012,51(4):1554-1566.
[6]NIELS J S,MUTASIM A S,NAIM A K.Energy management strategies for parallel hybrid vehicles using fuzzy logic[J].Control Engineering Practice,2003(11):171-177.
[7]何玮,刘昭度,杨其校,等.汽车嵌入式 SoC系统的应用与发展[J].电子技术应用,2005,31(4):18-21.
