基于全散度的C-V模型阈值法*

王继策，王 慧，吴成茂

(西安邮电大学 电子工程学院，陕西 西安 710121)

0 引言

图像分割作为实现图像识别与理解的基础，一直是计算机视觉领域研究的热点。尽管图像分割算法已经研究了数十年，但由于图像的复杂性、多样性，至今没有一个通用的分割理论和算法。因此，人们一直在不断寻找新的分割方法，以便获得满意的分割效果。

在图像分割方法中，阈值法是一类广泛应用的方法，其关键是如何选取最佳分割阈值。在众多阈值方法中，Otsu阈值法[1]是基于最大类间方差的全局阈值法，它具有简单、快速、性能稳定等特点。但全局阈值法对光照不均匀图像很难获得满意的分割结果。

近年来，参考文献[2]提出了基于区域的几何活动轮廓分割模型（即C-V模型），其利用水平集理论[3]可获得该模型求解算法，由于C-V模型具有全局分割能力、对弱边缘图像具有较好的分割结果等优点，因而得到广泛研究与应用。但是，C-V模型对灰度不均匀图像的分割仍存在失效且收敛速度慢的缺点。对此，参考文献[4]提出了逆浓度扩散模型，并给出基于直方图的Mumford-Shah模型快速阈值分割算法。

针对传统C-V模型无法较好分割灰度不均匀图像的问题，本文将全散度(Total Bregman Divergence，TBD)[5]理论引入传统C-V模型，获得TBD-CV模型来刻画像素值与分割区域平均像素值大小的差异性；之后，采用水平集理论和变分法获得具有较好鲁棒性、抗噪性的数值迭代分割算法；最后，利用灰度级统计直方图对模型进行简化，获得高性能快速阈值分割算法，并通过实验验证TBD-CV模型的有效性。

1 理论背景

1.1 Bregman散度与全散度

散度是信息论与信息几何中非常重要的概念，它是度量两个随机变量概率分布差异、空间对象差异的重要量，它与信息熵之间存在着紧密关系。散度理论已广泛应用于聚类分析、图像分割、图像检索、数据编码与压缩等众多领域，现已成为智能信息处理等问题的重要解决工具。传统平方欧式距离是最常用的Bregman散度，它是度量差异性的基本方法，但它的计算值与坐标系选取的紧密相关，且该度量对奇异数据点的计算缺乏鲁棒性，导致将其用于灰度不均或有噪声图像分割时，易出现错分现象问题。为此，本文引入了全散度理论。

定义1[6]：Bregman散度 设可微函数f是严格凸函数，x、y是函数上两个不同的点，则 Bregman散度 df(x，y)可通过下面的公式给出：

其中，▽f(y)是在 y 上计算的函数 f的梯度；〈x-y，▽f(y)〉是▽f(y)和(x-y)的内积，对于欧式空间的点，内积即为点积。

定义 2[5]：全散度 设可微函数 f是严格凸函数，x、y是函数上两个不同的点，则全散度δf(x，y)可通过下面的公式给出：

式中，〈·，·〉同定义 1 中，为内积。

从图1所示的Bregman散度与全散度的示意图来看，若函数关系不变，将坐标系做一定的旋转，此时df(x，y)值发生了变化。而δf(x，y)值却保持不变。现假设所求函数关系 f(x)=x2，则式(1)、式(2)化简为：

图1 Bregman散度与全散度示意图

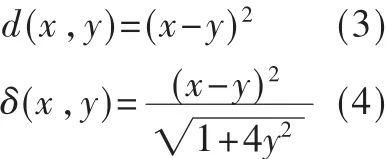
1.2 C-V模型

在图像中，对象与背景的区别一般表现为平均灰度值的明显不同。对于此类边缘、纹理等特征不明显的图像，假设能找到闭合曲线C，它使全部图像域划分为内部区域 Ω1和外部区域 Ω2两个分部，使在 Ω1内的图像部分与在Ω2的图像部分的平均灰度恰好反映出图像对象与背景之间的灰度平均值的差别，那么这一闭合曲线就可以看成是所要分割对象的轮廓。基于这一思路，Chan和 Vese[2]提出了如下“能量”泛函，即C-V模型：

其中，令 Ω⊂R2为有界开子集，I：Ω→R为给定灰度图像且满足 I(x，y)：x，y∈Ω，C 为演化曲线，Ω1、Ω2分别为演化曲线的内部区和外部区，c1、c2分别为演化曲线内、外部的灰度平均值，参数 μ，υ≥0，权重系数 λ1，λ2＞0。

2 TBD-CV模型

C-V模型是基于区域信息的几何活动轮廓模型，它克服了基于边缘的几何活动轮廓模型的全局性差和不易分割弱边缘的不足。但是C-V模型分割算法采用的是欧氏距离，仅将灰度同质作为区域分离的准则，只能用于包含目标和背景两个不同均值区域的高对比度图像分割中，对非均匀性或有噪声干扰图像的分割并不太理想。而全散度是计算可微凸函数的一点与其另一点切线的正交距离，其计算与坐标系的选择无关，将其应用到分割算法中，可以有效避免噪声干扰的影响.

2.1 改进的全散度

为了将Bregman散度与全散度统一，本文提出一种改进的全散度，使得其散度应用具有更好的普适性，定义如下：

式中，η≥0。 当 η=0时，式(6)退化为 Bregman散度；当η=1时，式(6)即为全散度。

2.2 本文模型

本文基于全散度理论，提出一种改进的图像分割模型，该模型很大程度上提升了对灰度不均匀或有噪声污染图像的分割能力。现引入水平集函数φ，对TBD-CV模型能量泛函定义如下：

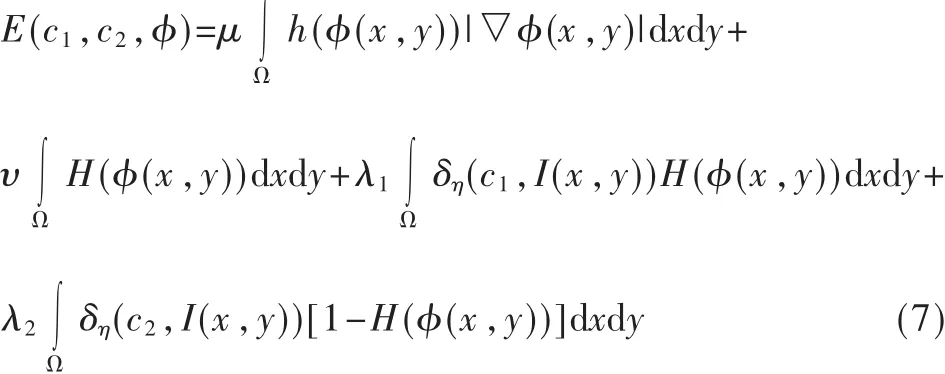
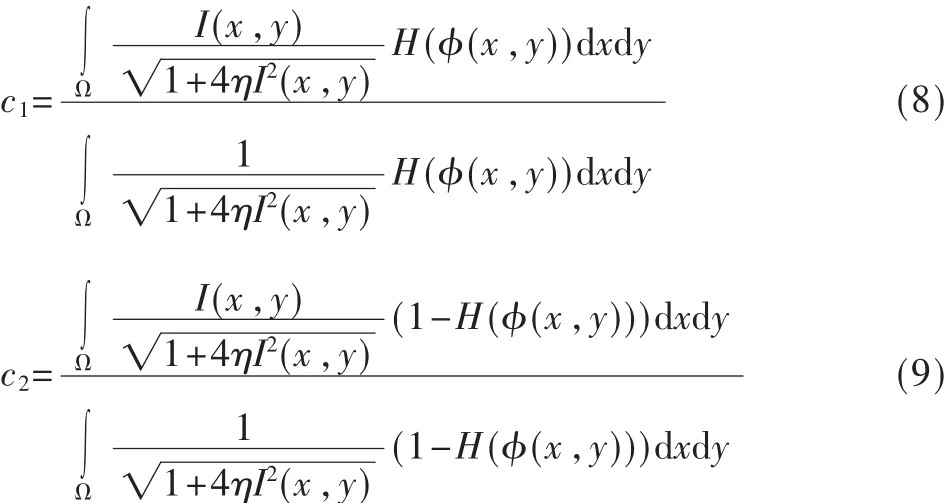
2.3 数值算法

根据欧拉—拉格朗日变分法，在将曲线演化应用于图像处理问题时，曲线运动方程来自于最小化闭合曲线C的能量泛函式(7)，得到如下方程：

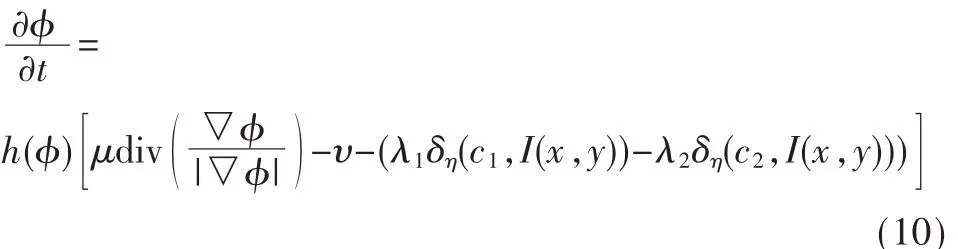
其对应迭代方程为：

在实验过程中， 令 υ=0，λ1=λ2=1。 根据参考文献[7]中指出 h可用▽φ替换，而▽φ≈1，同时是起到光滑分割曲线的作用，但在实际计算中起到的作用相对很小，且计算量很大，所以本文忽略该项。于是，式(10)可简化为：

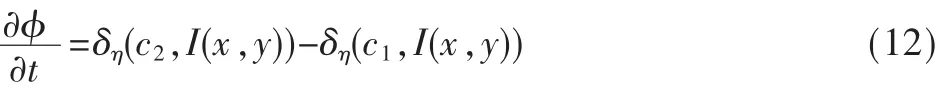
从式(12)可以看出，最终的分割结果只取决于图像的灰度信息，而与图像的具体灰度分布没有任何关系。因此，本文将直接利用直方图来简化计算。首先，将函数φ(x，y)映射为 φ(i)，其中 i=0，1，…255 为灰度值，令图像中灰度值为i且 φ(i)＞0的像素点为分割曲线内部 Ω1的像素点；反之，为分割曲线外部Ω2的像素点。

设图像直方图值为hist(i)，则式(11)可简化为：

同时，式(8)、式(9)也变为：

该方法所对应的图像阈值化分割算法步骤如下：

(1)获取图像I并计算图像灰度级直方图值hist(i)，i=0，1…255；

(2)初始化一维距离函数 φ0(i)=i-k，i=0，1…255，k∈[0，255]，k 值 采用 Otsu 算 法[1]获取；

(3)依据式(13)进行迭代计算，直到sign(φn)=sign(φn-1)；

(4)计算完成后，依据式(16)输出分割结果图像。

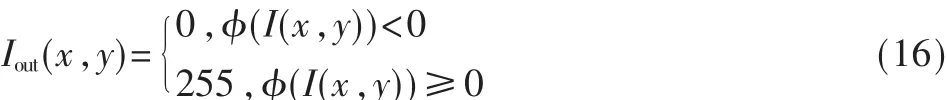
3 实验结果与分析

针对本文所建议的TBD-CV变分阈值分割模型，当参数η=0时，该分割模型退化为传统欧氏距离C-V模型；当参数η=1时，该分割模型即TBD-CV模型。

在分割实验中，选取 H函数的 ε=0.173，迭代时间步长▽t=0.1。为了降低初始值对分割模型的影响，采用经典Otsu阈值法获取区域中心c01、c02的初值。

从图2所示的细菌图像分割结果来看，原图像灰度不均匀，采用传统C-V模型所获得分割结果(图2(b)所示)目标细菌轮廓不清晰，甚至个别细菌出现断裂现象。采用TBD-CV模型分割结果如图2(c)所示，目标完全能从背景中提取且错分像素非常少，目标边界轮廓清晰。

图2 灰度不均图像测试图

为了测试分割模型对含噪声图像分割的鲁棒性，进行噪声干扰测试，如图3所示，图(a)为螺丝钉图添加一定零均值高斯噪声的图像，其噪声均方差为10；图(b)为C-V模型分割结果图，其分割结果背景受噪声影响，出现较多白点，即错将背景分割为目标现象；图(c)为TBD-CV模型分割结果图，其分割结果正确，目标清晰，且噪声干扰小。

图3 噪声干扰测试图

另外，为了客观评价不同分割算法的性能差异，本文引入被分割图像的实际分割结果与理想分割结果之间差异性度量的误分率 (Ratio of Segmentation Error,RSE)进行量化评估，定义如下：

表1 分割模型测试数据对比表

4 结论

从表1所示的两种分割模型的收敛迭代次数、时间消耗以及分割结果误分率来看，与传统欧式距离的变分CV分割模型相比，TBD-CV变分分割模型具有如下优点：(1)提高模型对灰度不均匀、噪声干扰图像的分割能力；(2)对噪声干扰图像具有一定的鲁棒性；(3)其阈值分割方法具有收敛速度快、耗时短的特点。因此，本文所建议的TBD-CV变分分割模型具有一定的普适性.

[1]OTSU N.A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems，Man，and Cybernetics，1979，9(1)：62-66.

[2]CHAN T F，VESE L A.Active contours without edges[J].IEEE Transactions on Image Processing，2001，10(2)：266-277.

[3]OSHER S，SETHIAN J A.Fronts propagating with curvature dependent speed：algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics，1988，79(1)：12-49.

[4]钱海勇，周卫平，鲍旭东，等.基于逆浓度扩散及直方图的Mumford-Shah模型的MRA血管分割[J].信号处理，2007，23(2)：273-277.

[5]LIU M Z，VEMURI B C，AMARI S I，et al.Shape retrieval using hierarchical total Bregman soft clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(12)：2407-2419.

[6]BANERJEE A，MERUGU S，DHILLON I S，et al.Clustering with Bregman divergences[J].The Journal of Machine Learning Research，2005(6)：1705-1749.

[7]LI J，YANG X，SHI P F.A fast level set approach to image segmentation based on Mumford-Shah model[J].Chinese Journal of Computer，2002，25(11)：1175-1183.