随机孔径对非均质多孔泡沫材料渗透性影响的数值模拟

王济平，张新铭，王 龙

（1.中电投远达环保工程有限公司，重庆401122；2.重庆大学低品位能源利用技术及系统教育部重点实验室，重庆400040）

0 引 言

高孔隙率多孔泡沫材料具有高比表面积、低表观密度、结构与功能一体化等优点，是一类具有潜在应用前景的新型工程材料［1］。多孔泡沫材料内流体的扩散过程广泛存在于化工、能源、环境和生物工程等领域，如航空系统、地热系统、机载设备的紧凑型散热器、汽车尾气处理、工业污水处理、蒸馏工业、电子设备热沉、微型系统热管理等［2-4］。

关于多孔泡沫材料渗透性的研究已有大量文献报道［5-10］。但现有的研究通常将孔隙率作为影响渗透率的参数，其前提是假定泡沫材料是均质的，即孔隙结构规则、周期性分布。然而，实际上多孔泡沫材料大都是非均质的，孔隙结构不均匀性等会对多孔泡沫材料的性能有着重要的影响［11-13］。

为此，作者基于随机孔径的面心立方体单元，建立了非均质多孔泡沫材料随机模型，对孔隙内空气的流动过程进行数值模拟，引入孔隙均匀度作为表征孔径随机分布的参数，讨论当孔径尺寸不均匀时，孔隙结构随机性对非均质多孔泡沫材料渗透性的影响，提出了非均质多孔泡沫材料渗透率与孔隙率、孔隙均匀度的函数关系式。

1 计算模型

1.1 几何模型

以多孔石墨泡沫为例，建立几何模型。由图1可以看出，多孔石墨泡沫的孔隙尺寸分布得相当不均匀。采用面心立方体单元表征非均质石墨泡沫的孔隙。设单元边长为a，随机孔径为ds，定义无量纲孔径d＊＝ds/a，根据多孔泡沫材料的结构特点，为保证泡沫材料内部固体骨架相连且孔隙相通，则d＊的取值范围为

根据式（2）可计算出对应单元孔隙率φ的范围为0.523 6＜φ ＜0.965 1。

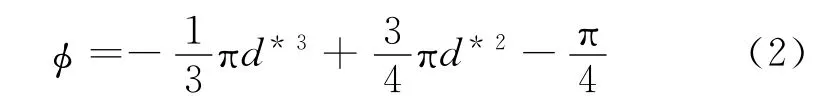
材料的比表面积β，即固流两相界面面积与材料表观体积之比，则可表示为

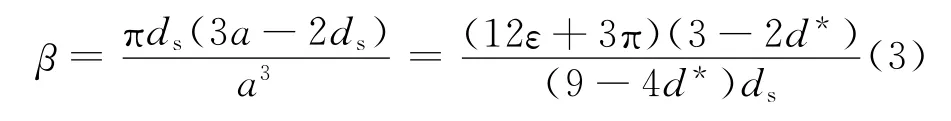
式中：ε为泡沫模型的平均孔隙率（以下称孔隙率）。

图1 多孔石墨泡沫的SEM形貌Fig.1 SEM morphology of porous graphite foam

通过APDL编程，定义随机孔径ds，人工随机建立非均质多孔泡沫材料的几何模型，如图2所示，采用有限元分析软件Ansys对孔隙内空气的流动过程进行数值模拟。

1.2 孔隙均匀度

为描述非均质泡沫材料孔隙结构的随机性，定义基于局部孔隙率的孔隙均匀度U：

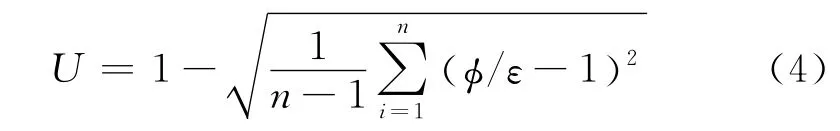
式中：n为孔隙总数。

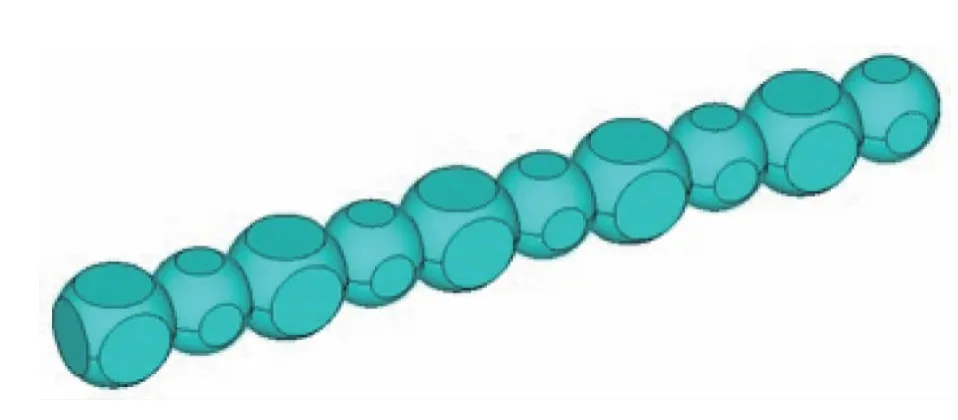
图2 非均质多孔泡沫材料的模型Fig.2 Model of heterogeneous porous foam

孔隙均匀度U∈（0，1］表征了各单元局部孔隙率与泡沫模型平均孔隙率的偏差统计值。U值小于1时，泡沫材料为非均质的。U值越小，说明模型的结构随机性越大，孔隙结构越不均匀；U值越大，则模型的结构随机性越小，孔隙结构越均匀。U值等于1时，泡沫材料为完全均质的。

1.3 控制方程和边界条件

连续性方程和动量方程分别为

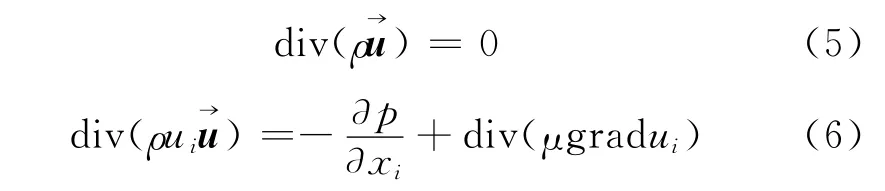
以空气进口流速和出口压力为边界条件，空气入口速度均匀分布，入口流速范围为0～7m·s-1；出口边界为自由出口，相对压力为0；气固接触面为非滑移边界条件。应用Ansys有限元软件进行数值模拟，划分网格数量约300 000，并进行了网格无关性验证。

2 模拟结果与分析

由图3可以看到，均质泡沫材料中的压力梯度（Δp/L）随材料截面上空气流速（u）增大而增大，随孔隙率（ε）增大而减小，满足 Ergun［14］方程：

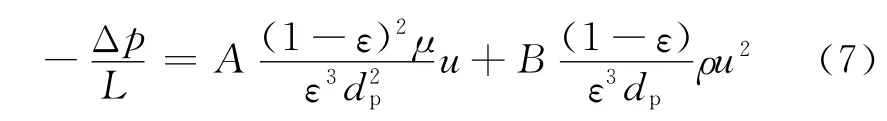
式中：μ为流体动力黏度，kg·m-1·s-1；dp为球形颗粒直径，mm；A 和B 均为常数，A＝150，B＝1.75。

由图4可见，泡沫材料中的Δp/L随着u的增大而增大；但Δp/L还与孔隙均匀度有关，U越大则Δp/L越大，即孔隙结构越均匀，流动阻力越大，说明孔隙率已不是非均质多孔泡沫材料唯一的结构参数，孔隙结构的不均匀性对其渗透性也有影响。这主要是因为孔隙结构的不均匀性使材料的比表面积发生变化所致。在相同的孔隙率下，非均质泡沫材料的β值小于均质泡沫材料的，从而导致流体与固体骨架表面的接触面积减少，摩擦减小，压降损失减小，因此材料的渗透性变好。

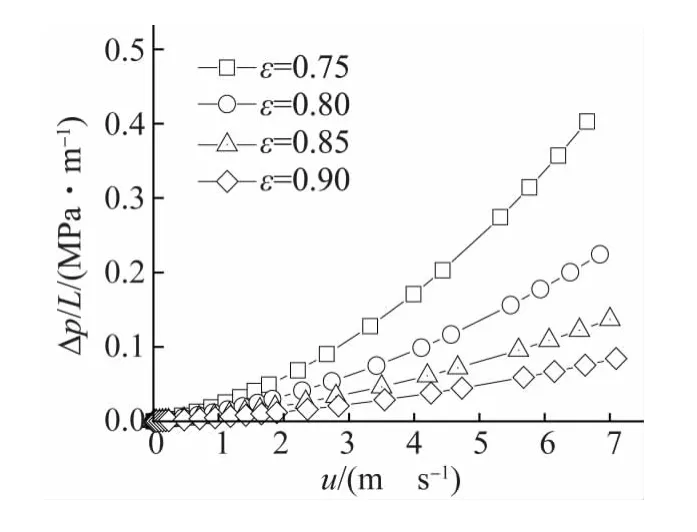
图3 不同孔隙率的均质泡沫材料中Δp/L与u的关系（U＝1）Fig.3 Δp/Lvs uin homogenous porous foams with different porosities（U＝1）

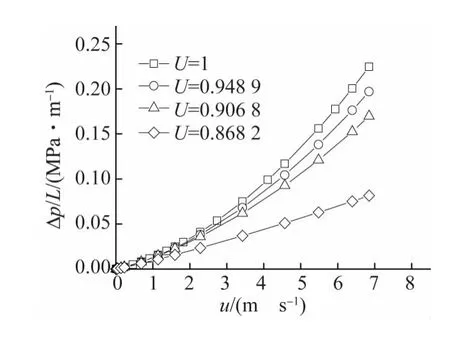
图4 不同孔隙均匀度的泡沫材料中Δp/L与u关系（ε＝0.8）Fig.4 Δp/Lvs uin porous foams with different pore uniformities（ε＝0.8）

由此可见，孔隙率和孔隙均匀度同时影响多孔泡沫材料的渗透性，孔隙率是平均意义的孔隙结构参数，而孔隙均匀度则是表征孔隙结构随机性的参数。

在较高空气流速下，多孔泡沫材料内的压力梯度遵循 Darcy-Forchheimer［15］关系式：

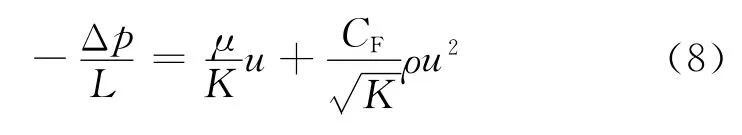
式中：K为渗透率；CF为惯性阻力系数。

由式（8）即可求得多孔泡沫材料的渗透率。均质泡沫模型（U＝1）的模拟结果如表1所示，且与文献报道结果进行了比较。可见，各均质材料模型结果趋势一致，渗透率随孔隙率的增大而增大，这与现有文献试验结果整体趋势相同，渗透率出现的偏差是因为选用了不同的模型及流速范围。另外，试验结果呈现出了一定的随机性，如文献［16］中ε＝0.86和文献［17］中ε＝0.857时的渗透率，以及文献［18］中ε＝0.919和文献［19］中ε＝0.92时渗透率。

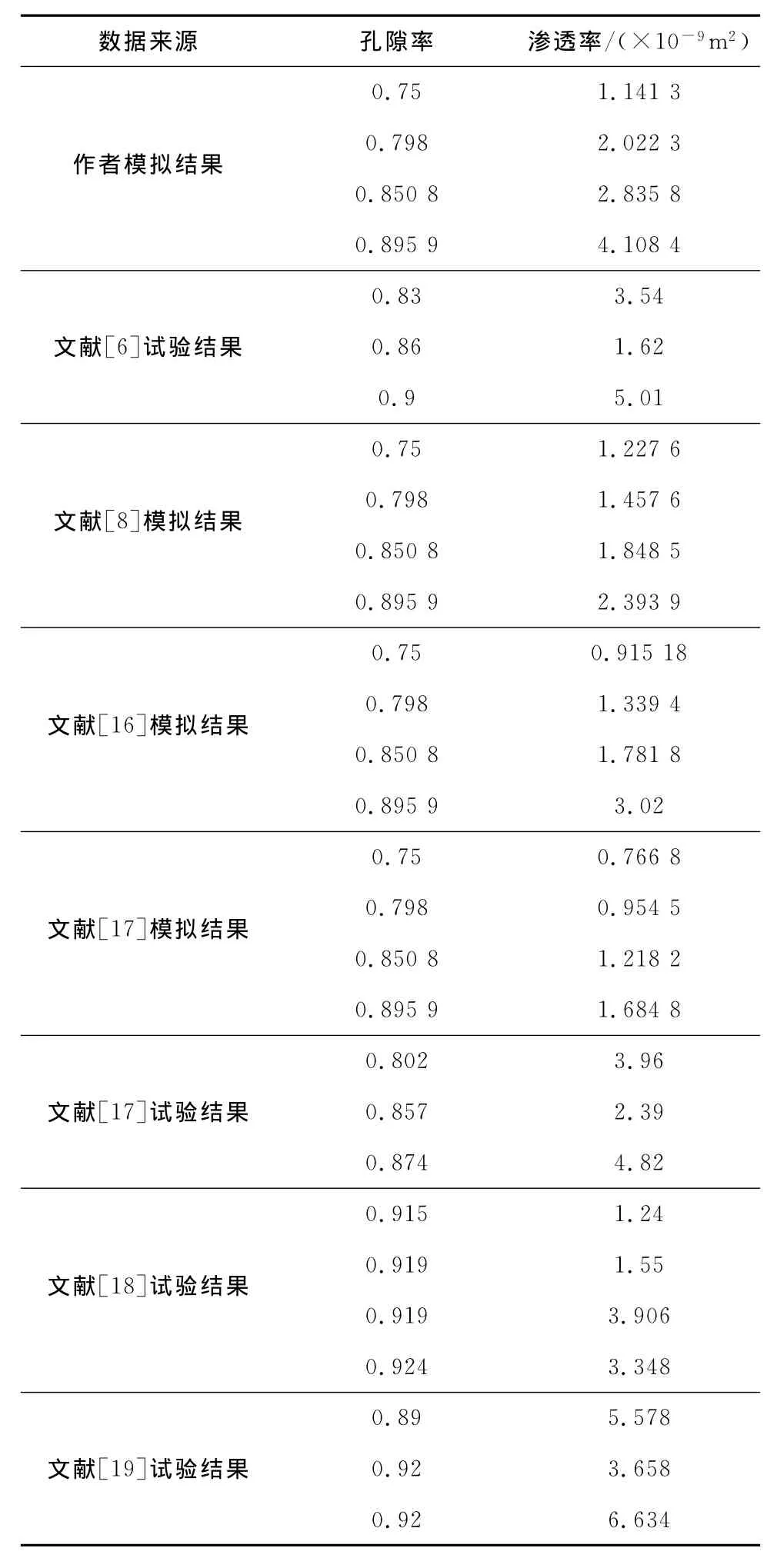
表1 均质多孔泡沫材料渗透率模拟结果与文献结果的比较Tab.1 Comparison of the simulated permeability of homogeneous porous foams with results from other references

由图5可见，在相同的孔隙均匀度下，渗透率随孔隙率增大而增大；在相同的孔隙率下，渗透率随孔隙均匀度的增大而减小，这很好地解释了表1中试验数据呈现出的随机性，因而本模型结果与参考文献的试验结果更加吻合，采用本模型预测非均质多孔泡沫材料的渗透率更为可靠。

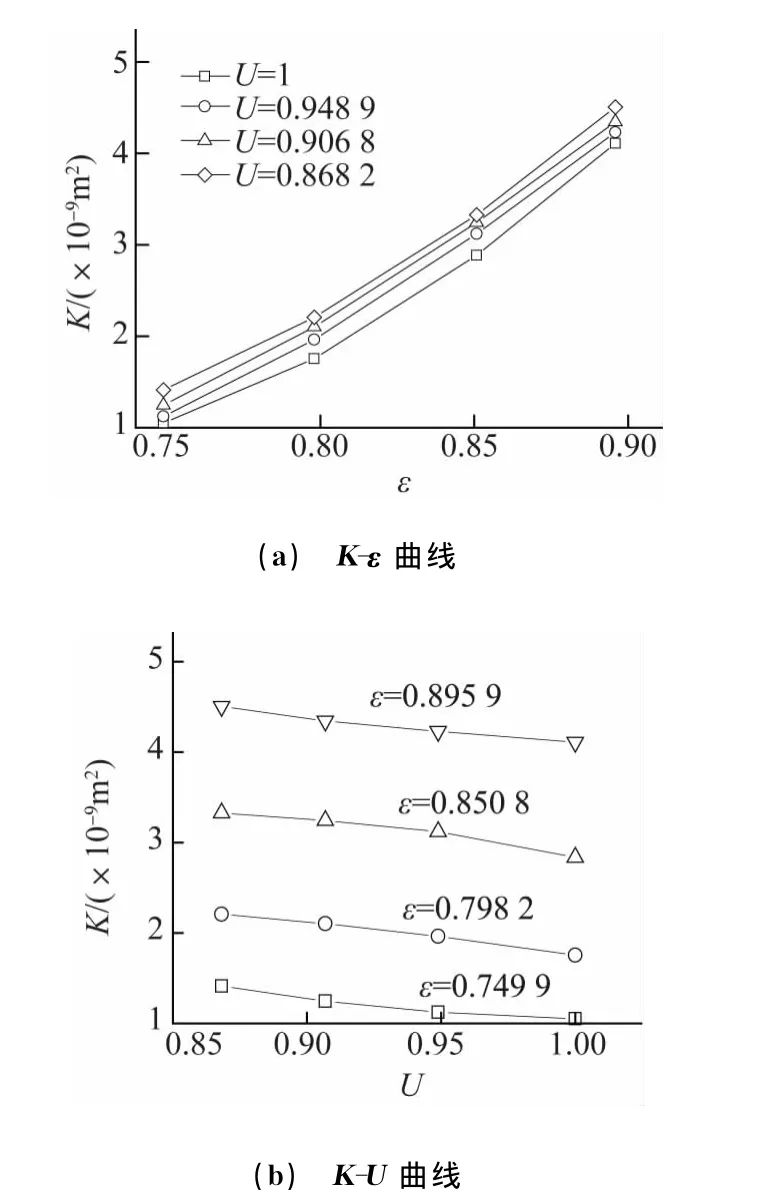
图5 非均质泡沫材料渗透率随孔隙率、孔隙均匀度的变化曲线Fig.5 Permeation rate vs porosity（a）and pore uniformity（b）in the heterogeneous porous foams

综上所述，渗透率K可定义为孔隙率及孔隙均匀度U的函数，即

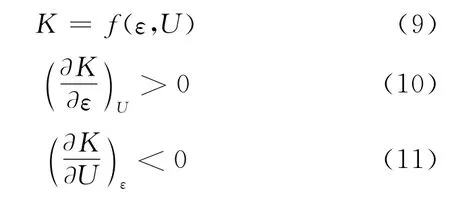
定义无量纲渗透率

K＊＝Kβ2/［6（1-ε）］2（12）

拟合得到非均质多孔泡沫材料渗透率与孔隙率及孔隙均匀度的函数式：

K＊＝0.664 1ε12.4026U-0.347（13）

分析计算得出此拟合式的计算值与模拟结果偏差在5%以内。

3 结 论

（1）流体流过非均质多孔泡沫材料时压力梯度满足Darcy-Forchheimer关系，在相同的孔隙均匀度下，压力梯度随着孔隙率的增大而减小，渗透率随孔隙率增大而增大；在相同的孔隙率下，压力梯度随着孔隙均匀度的增大而增大，渗透率随孔隙均匀度增大而减小；孔隙率和孔隙均匀度同时影响泡沫着材料的渗透性。

（2）模型的模拟结果相比可知，采用非均质随机模型的模拟结果与参考文献的试验数据更加吻合，除孔隙率外，孔隙结构的随机分布对材料渗透性也有影响，非均质泡沫材料渗透率如下幂函数表示K＊＝0.664 1ε12.4026U-0.347。

［1］王新筑，彭向和，郭早阳.泡沫铝准静态压痕响应的数值模拟［J］.机械工程材料，2013，37（4）：78-82.

［2］韩永生，李建保，魏强民.多孔陶瓷材料应用及制备的研究进展［J］.材料导报，2002，16（3）：262-269.

［3］高鑫，李鑫钢，魏娜，等.多孔介质泡沫材料在蒸馏过程中的应用［J］.化工进展，2013，32（6）：1313-1319.

［4］NIDIA C G，KLETT J W.Carbon foams for thermal management［J］.Carbon，2003，41（7）：1461-1466.

［5］DESPOIS J F，MORTENSEN A.Permeability of open-pore microcellular materials［J］.Acta Materialia，2005，53（5）：1381-1388.

［6］KHAYARGOLI P，LOYA V，LEFEBVRE L P，et al.The impact of microstructure on the permeability of metal foams［C］//Proceeding of CSME Forum.［S.l.］：［s.n.］，2004：220-228.

［7］BHATTACHARYA A，CALMIDI VV，MAHAJAN R L.Thermophysical properties of high porosity metal foams［J］.International Journal of Heat Mass Transfer，2002，45（5）：1017-1031.

［8］DUPLESSIS J P，MONTILLET A，COMITI J，et al.Pressure drop prediction for flow through high porosity metallic foams［J］.Chemical Engineering Science，1994，49（21）：3545-3553.

［9］DUKHAN N，PATEL P.Equivalent particle diameter and length scale for pressure drop in porous metals［J］.Experimental Thermal and Fluid Science，2008，32（5）：1059-1067.

［10］吕兆华.泡沫型多孔介质中非达西流动特性的研究［J］.工程力学，1998，15（2）：57-64.

［11］施明恒，虞维平，王补宣.多孔介质传热传质研究的现状和展望［J］.东南大学学报，1994，24（增1）：2-7.

［12］李小川，施明恒，张东辉.非均匀多孔介质有效热导率分析［J］.工程热物理学报，2006，27（4）：644-646.

［13］李莎，雍玉梅，尹小龙，等.多孔介质的孔隙特性对气体过程影响的直接数值模拟［J］.化工学报，2013，64（4）：1242-1248.

［14］ERGUN S.Fluid flow through packed columns［J］.Chemical Engineering Progress，1952，48（2）：89-94.

［15］KOPANIDIS A，THEODORAKAKOS A，GAVAISES E，et al.3Dnumerical simulation of flow and conjugate heat transfer through a pore scale model of high porosity open cell metal foam［J］.International Journal of Heat and Mass Transfer，2010，53（11）：2539-2550.

［16］LACROIX M，NGUYEN P，SCHWEICH D，et al.Pressure drop measurements and modeling on SiC foams［J］.Chemical Engineering Science，2007，62（12）：3259-3267.

［17］RICHARDSON J T，PENG Y，REMUE D.Properties of ceramic foam catalyst supports：pressure drop［J］.Applied Catalysis A：General，2000，204（1）：19-32.

［18］ DUHAN N.Correlations for the pressure drop for flow through metal foam［J］.Experiments in Fluids，2006，41（4）：665-672.

［19］KIM S Y，PAEK J W，KANG B H.Flow and heat transfer correlations for porous fin in plate-fin heat exchanger［J］.Journal of Heat Transfer，2000，122（3）：572-578.