连轧管机轧制力模拟与计算

赵 佳

(中冶京诚工程技术有限公司轧钢与金属加工工程技术所钢管部,北京 100176)

连轧管机轧制力模拟与计算

赵 佳

(中冶京诚工程技术有限公司轧钢与金属加工工程技术所钢管部,北京 100176)

本文在相同的技术条件下运用有限元模拟和数学公式两种方法对三辊连轧管机组轧制力进行了计算,叙述了两种方法的计算过程,对两种方法的计算结果同实际值进行了比较,并分析了各自优缺点与适用的范围。

三辊连轧管机 有限元模拟 数学公式 轧制力

1 引言

随着连轧管工艺技术的不断进步,尤其在第一套PQF三辊连轧管机组在天津建成以后,我国成为世界上无缝连轧管技术最先进的国家,先后有十余套三辊连轧管机组建成或在建。但这些机组的核心部分连轧管机都是采用进口,这与我国钢管大国的身份不符,为使我国由钢管大国变为钢管强国,我们在消化吸收的基础上自行研发三辊连轧管机组,这里首先运用有限元和数学公式的方法对轧制力进行计算。为设备设计及日后实际生产提供理论依据和技术支持。

2 计算用基本数据

2.1 孔型参数

孔型设计可以说一门专门的学科,需要综合考虑金属流动、变形分配等,这里只列出经过计算后得到的某263系列孔型的部分参数,如表2.1所示。孔型参数示意图如图2.1所示。

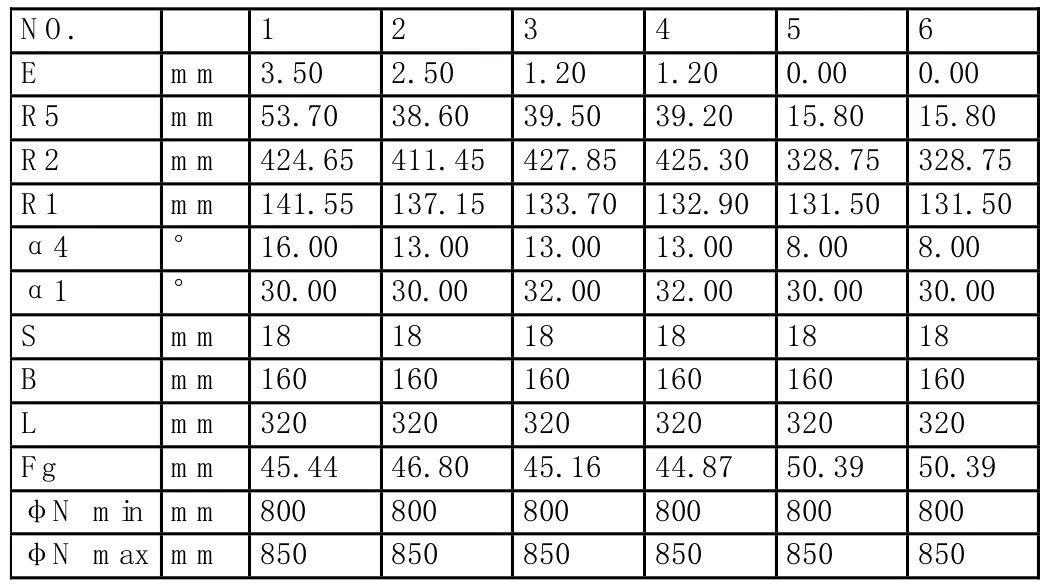
表2.1 263系列孔型参数

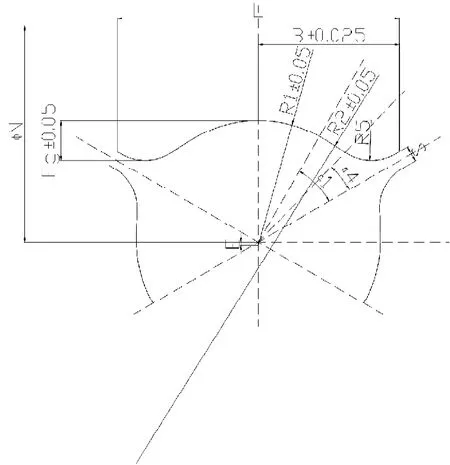
图2.1 孔型参数示意图

2.2 轧制钢种及材料特性

计算选用钢种为20#钢,材料的泊松比是0.3,材料密度为7.83×10-9t/mm3,材料的杨氏模量曲线如图2.2所示。

图2.2 杨氏模量随温度变化关系

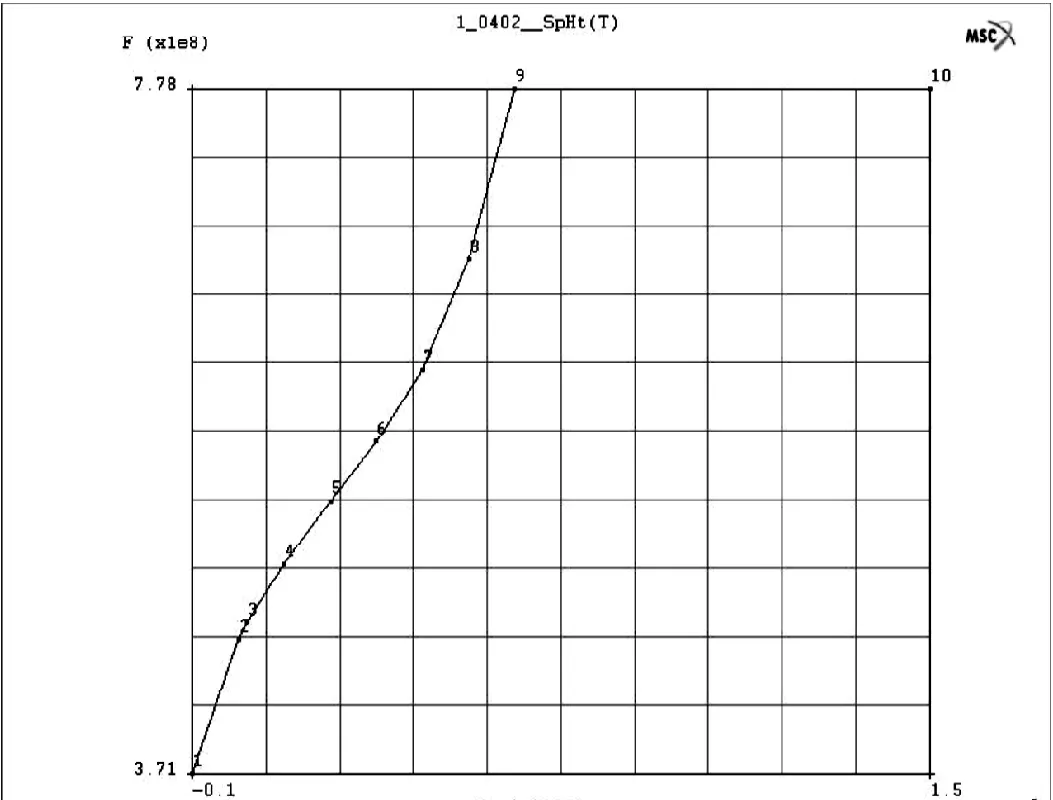
图2.3 比热容随温度变化关系

比热容随温度变化关系如图2.3所示。热膨胀系数随温度变化关系如图2.4所示。热导率随温度变化关系如图2.5所示。

2.3 计算初始条件

计算用毛管尺寸为306×29.25mm,初始温度为1150℃,芯棒尺寸234.5mm。热力学特性包括轧件与环境的等效换热系数为0.17kW/(m2·℃),热功转换系数为0.9,轧辊与轧件的接触换热系数为20kW/(m2·℃)。机械参数为摩擦系数为0.4,芯棒与轧件摩擦系数为0.07。各机架参数图表2.2所示。

3 有限元模拟计算

近年来随着计算机技术的普及和计算速度的不断提高,有限元分析在工程设计和分析中得到了越来越广泛的重视,已经成为解决复杂的工程分析计算问题的有效途径,现在从汽车到航天飞机几乎

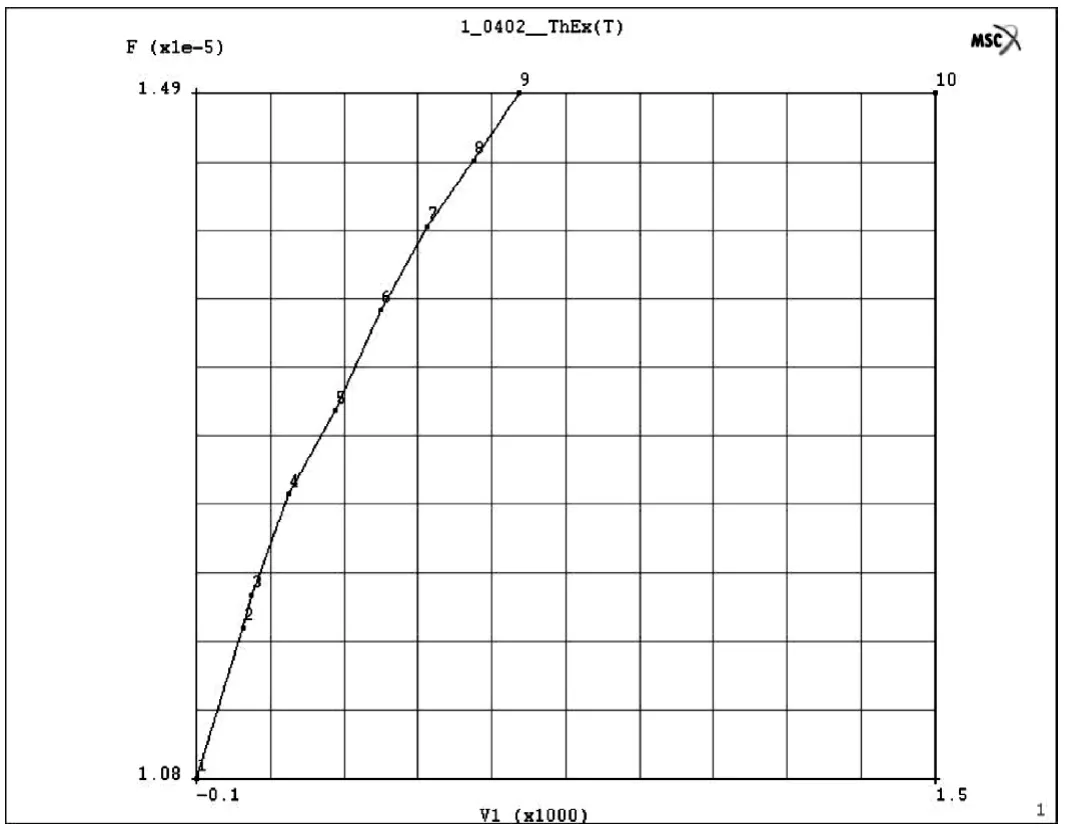
图2.4 热膨胀系数随温度变化关系

图2.5 热导率随温度变化关系

所有的设计制造都已离不开有限元分析计算。无缝钢管生产过程也是如此。通过各种有限元软件对钢管的钻孔、轧制、张减径、定径等生产的各个过程都有研究。

MSC.Marc是国际上通用最先进的非线性有限元分析软件之一,具有极强的结构分析能力,对于钢管轧制这种复杂的大变形多场耦合情况,使用Marc进行模拟是最为合适的。

图3.1为建立的有限元几何模型。

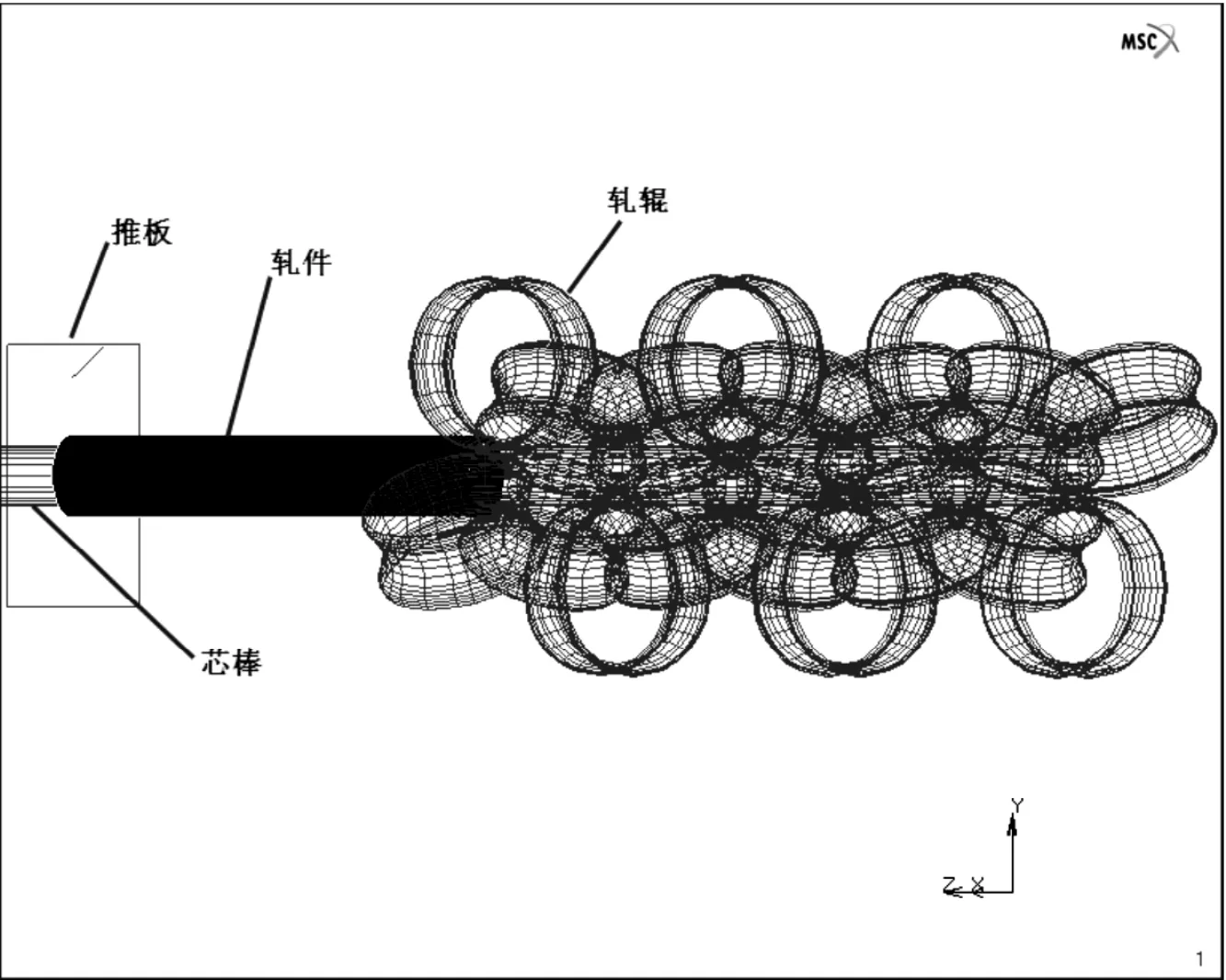
图3.1 有限元方法几何模型

运用有限元模拟软件Marc对前述条件下的毛管轧制过程进行模拟计算,得到各机架处金属等效Mises应力分布如图3.2所示。

图3.3为有限元软件模拟得到的轧制力曲线,实线为平均后的轧制力曲线。

各机架稳定轧制时平均轧制力如表3.1所示。

表2.2 各机架主要参数

4 数学公式方法计算

数学公式的方式是运用二辊的计算思路,考虑到三辊与二辊的区别,现对三辊连轧管机的轧制力进行试算。

4.1 所需参数

(1)孔型K

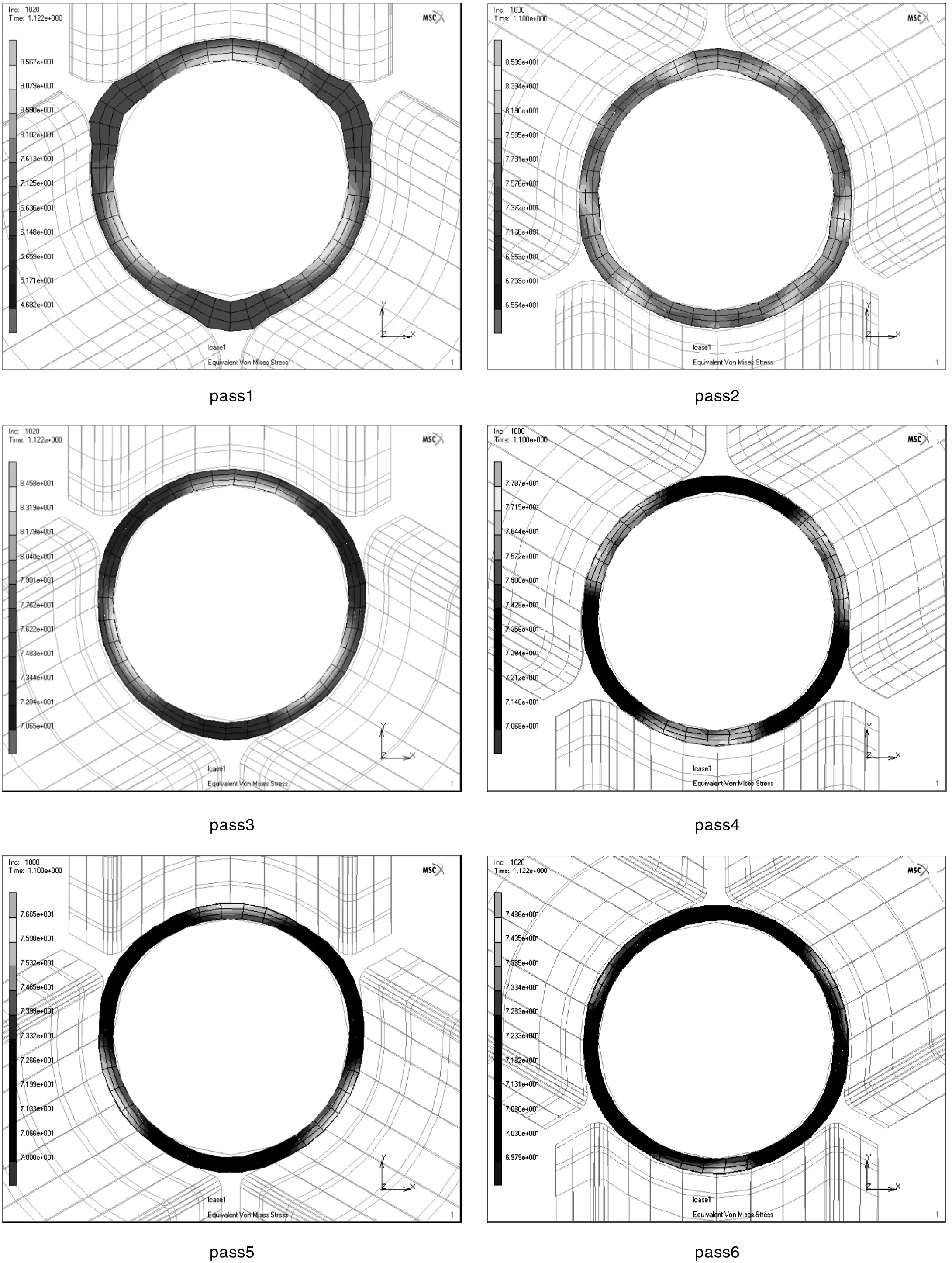
图3.2 各机架等效Mises应力分布

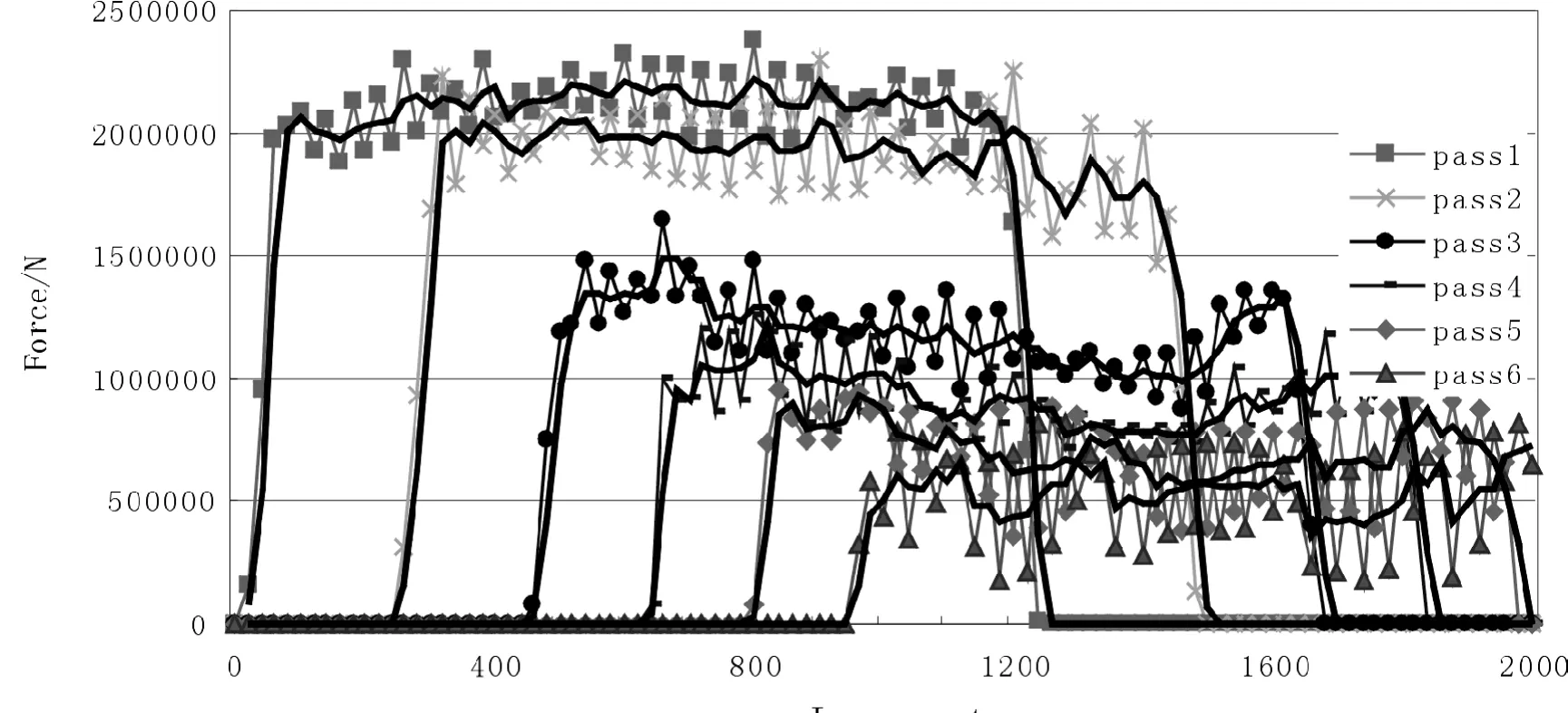
图3.3 有限元模拟轧制力分布曲线

表3.1 有限元模拟平均轧制力

图4.1 钢管轧制等效为钢板轧制示意图

图4.2 轧后钢管截面积示意图

图4.3 力平衡和塑性方程单元体示意图

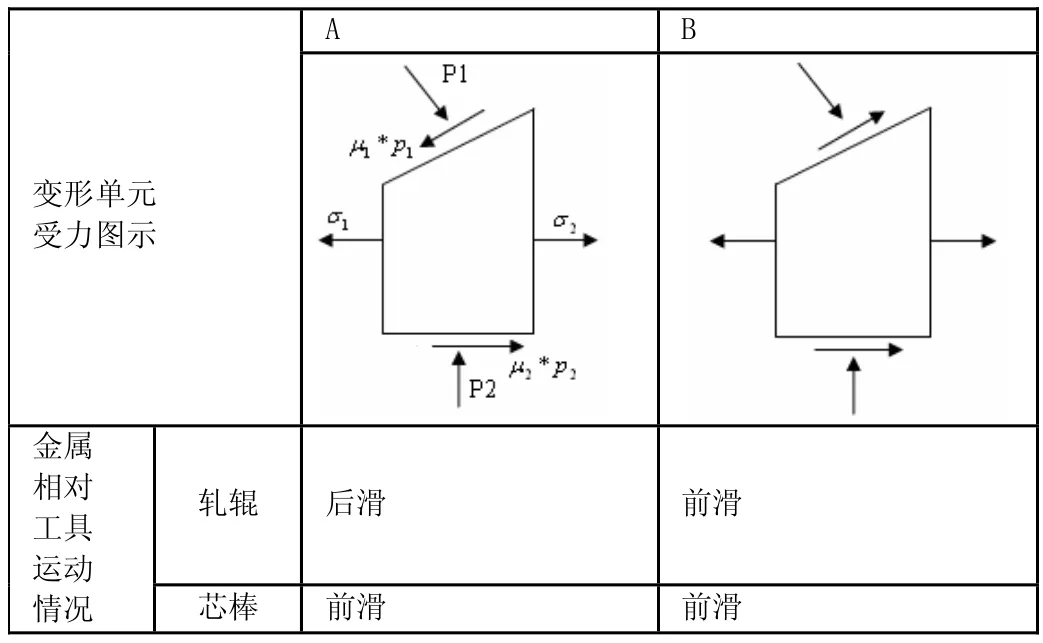
表4.1 钢管连轧过程中的单元受力情况

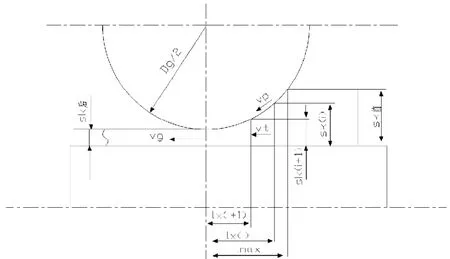
图4.4 轧件与轧辊、轧件与芯棒相对速度关系示意图

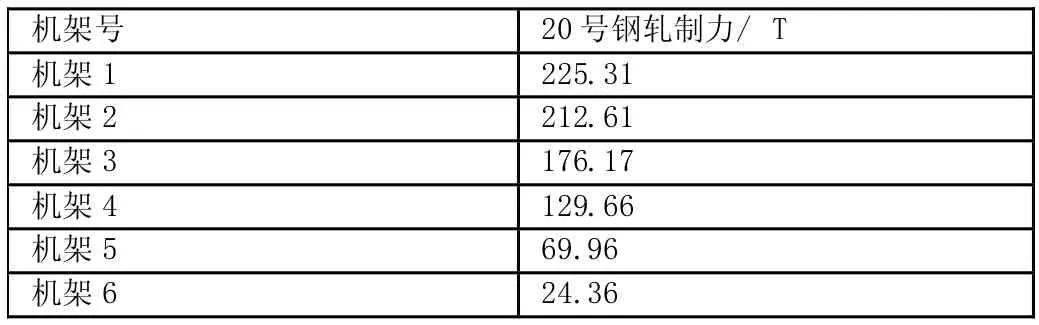
表4.2 数学计算结果

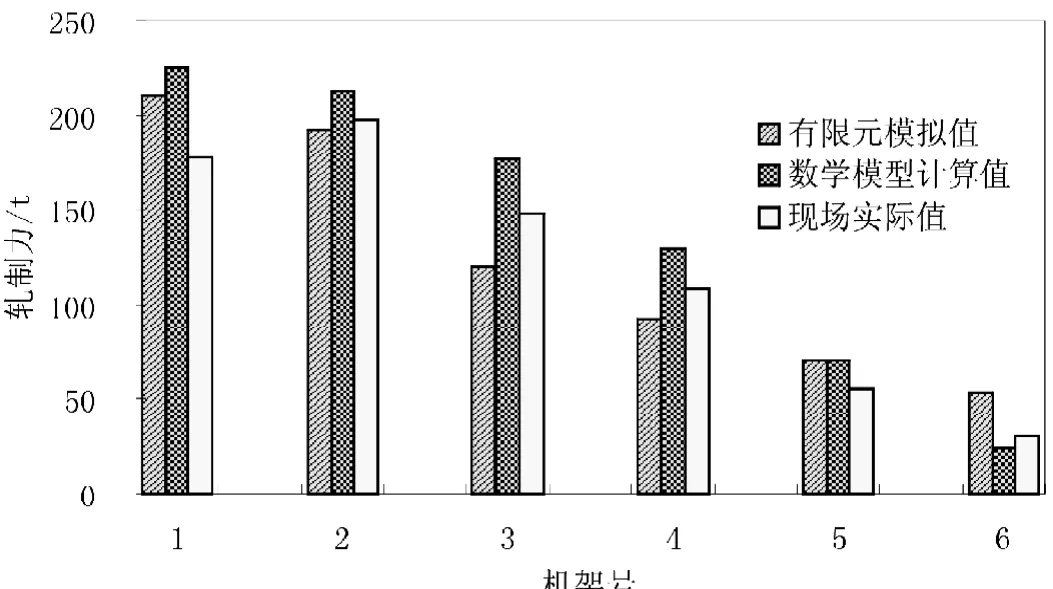
图5.1 不同方法得到的轧制力比较

由孔型所决定的变量包括:所有孔型的相关参数。(2)材质C

由材质所决定的变量包括:变形抗力σ。

(3)毛管外径Ds

(4)毛管壁厚SKs

(5)芯棒直径dc

(6)开轧温度t1

(7)终轧温度t2

(8)轧辊直径D

(9)轧件与轧辊摩擦系数1μ

(10)轧件与芯棒摩擦系数2μ

(11)末机架管子出口速度vg

4.2 建模思路

传统钢管轧制力的计算方法着眼于钢管轧制过程中的变形区投影面积和单位压力,相乘后得到钢管轧制力。由于钢管轧制过程变形十分复杂,因此计算过程非常繁琐,但计算结果并不理想。为了使计算过程简单、灵活,数学模型中把钢管轧制假设为等效钢板的轧制,如图4.1所示。

4.2.1 等效钢板轧辊直径的确定

等效钢板轧辊直径取值为钢管轧辊的工作辊径Dg。对于三辊连轧管机Dg可近似计算如式1.1。

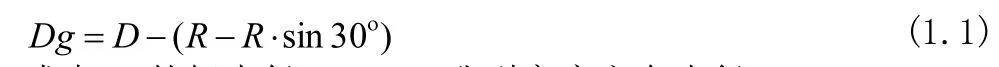
式中D:轧辊直径,mm;R:孔型高度方向半径,mm。

4.2.2 等效钢板轧后壁厚的确定

等效钢板轧后壁厚的取值为钢管轧后的平均壁厚。在CAD中将孔型画出,则由孔型、轧前钢管外径、芯棒外径所界定的区域近似等于轧后钢管的截面积,令轧后钢管以芯棒直径为内径,面积等于该区域面积,如图4.2所示。列方程后可得到轧后钢管的平均壁厚,如式1.2所示。该过程中忽略了钢管与芯棒的间隙及孔型开口处的壁增厚现象。

式中F:轧后钢管截面积,mm2;SK后:轧后平均壁厚,mm;dh:热态芯棒直径,dc为冷态芯棒直径,mm。

4.2.3 等效钢板轧前壁厚的确定

通过4.2.2的计算,等效钢板轧前壁厚等于钢管的轧前平均壁厚,即上一机架钢管的轧后平均壁厚。

式中SKs:毛管壁厚,mm。

4.2.4 等效钢板板宽的确定

由于钢管的轧前、轧后壁厚均取了平均壁厚,可等效为沿周向均匀的压下,则接触角取为120°。等效钢板板宽B的确定如式1.6。

4.3 轧制力影响因素的确定

4.3.1 钢管连轧时的不同受力状态

在三辊限动芯棒连轧管过程中,金属处于轧辊和芯棒两个速度不同的工具中轧制,两工具与金属间产生不同的相对运动。由于芯棒速度被限定低于第一机架管子速度,金属相对芯棒总是前滑,则轧制过程中就会出现两种受力情况,在A情况下,金属相对轧辊后滑;在B情况下,金属相对轧辊前滑。如表4.1所示。

4.3.2 受力单元的力平衡和塑性方程

将金属与轧辊接触长度的投影按入口到出口的方向划分为100等份。则以A情况单元体为例,其受力如图4.3所示,列出单元体的力平衡和塑性方程。

轴向力平衡:

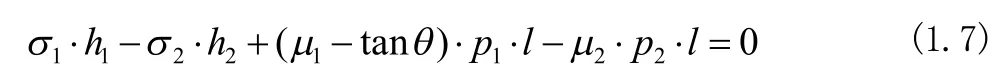
垂直方向力平衡:

塑性条件:

式中1μ:金属与轧辊间摩擦系数;2

μ:金属与芯棒间摩擦系数;

σ:金属变形抗力,MPa;

l:单元体长度,mm。

将式1.7、1.8、1.9联立后,令

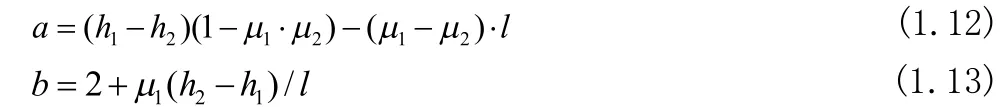
得:

计算过程中假设处于理想状态,机架间无张力,则出口处σ1=0,可分别求得σ2、p1、p2。对于下一单元体,采用迭代的方法计算直至入口断面,从而计算出p1、p2。

4.3.3 摩擦系数的确定

通过对单元体的受力分析,在轧制力的计算过程中需确定金属与轧辊间的摩擦系数1μ和金属与芯棒间摩擦系数2μ。通过查阅相关资料,在计算过程中,1μ取值为0.3。2μ的取值为0.07。

在对A单元体的受力分析过程中,金属相对于轧辊后滑,相对于芯棒前滑,则在方程的求解过程中1μ和2μ直接代入以上值。在另一受力情况下,金属相对于轧辊前滑,摩擦力的方向相反,则在方程的求解过程中1μ代入-0.3即可。

4.3.4 金属变形抗力的确定

利用已有的变形抗力模型,确定金属的变形抗力。传统的变形抗力模型如式1.17所示。式中0σ:基准变形抗力,即t=1000℃,时的变形抗力,MPa;

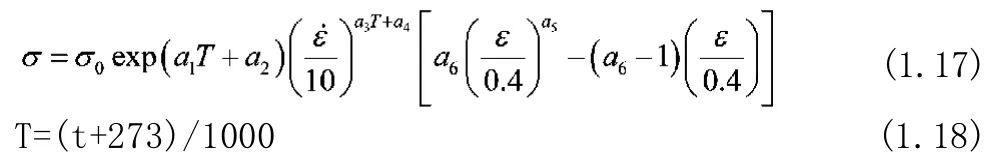
t:变形温度,℃;

ε:变形程度(真应变);

ε·:变形速率,s-1;

a1～a6:回归系数。

4.3.4.1 变形温度的确定

在轧制力的计算过程中,近似认为机架间温降相等,则各机架间的温降△t如式1.19。

式中t1:开轧温度;

t2:终轧温度;

n:机架数。

4.3.4.2 变形程度的确定

各机架变形程度ε如式1.20所示。

4.3.4.3 变形速率的确定

各机架变形速率·ε由式1.21所示。

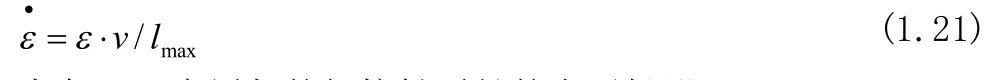
式中lmax:金属与轧辊接触弧长的水平投影,mm;

v:轧件平均速度,mm/s。

式中vg:轧机出口处轧件速度,mm/s。

4.3.5 钢管连轧时不同受力状态的确定

在钢管的连轧过程中,某一单元体处于哪种受力状态是通过计算管子与轧辊、管子与芯棒的相对速度后确定的。轧件与轧辊、轧件与芯棒相对速度关系的示意图如图4.4。

在一般情况下,金属在轧制过程中的前滑值平均波动在2～10%之间,计算过程中统一取前滑值为5%,则轧机出口处轧件速度vg如式1.23所示。

式中vp:轧辊线速度,mm/s。

已知末机架管子出口速度及各机架的横截面积,则可计算出各机架管子出口速度。

则图4.4中所示某单元体的速度vt如式1.24所示。

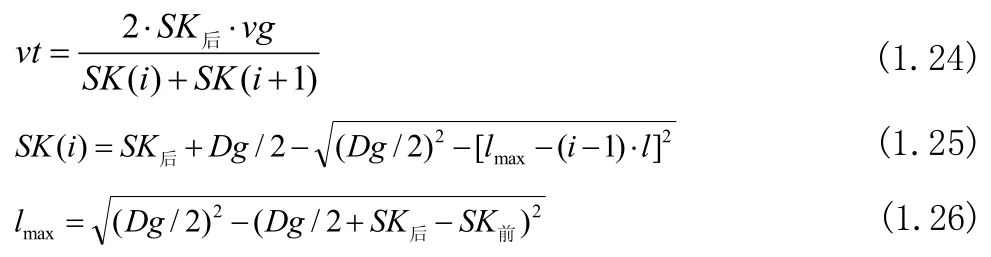
式中lmax:金属与轧辊接触弧长的水平投影,mm

l:单元体长度,l=lmax/100,mm。

则变形区内某一单元体管辊相对速度vx如式1.27所示。

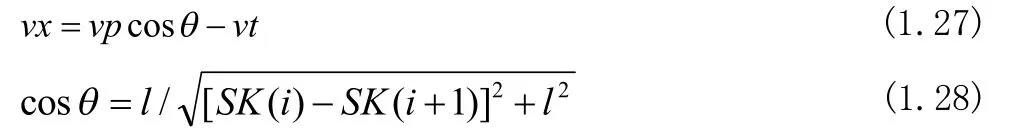
当vx〉0时,金属相对轧辊后滑;当vx〈0时,金属相对轧辊前滑。

在稳定轧制阶段芯棒的速度小于机架1的轧件速度,则所有机架中轧件相对芯棒前滑。

4.4 轧制力的计算

轧制力是轧制时轧辊施加于轧件使之变形的力,但通常把轧件施加于轧辊总压力的垂直分量称为轧制力。则在钢管轧制等效为钢板轧制后,轧制力应考虑到垂直分量的影响,所以乘以系数0.866。

根据以上分析计算,轧制力P的计算如式1.29所示。

4.5 数学公式计算结果

对前述的20号钢毛管进行计算得到的结果如表4.2所示。

5 结语

(1)不同方法得到的轧制力如图5.1所示。从图中可以看出,有限元模拟和数学公式计算得到的轧制力值与实际生产测得的轧制力基本相符,总体趋势相同,模拟值大体与实际值相等或偏小,数学公式计算值比实际值偏大。

(2)有限元软件模拟和数学公式计算作为不同的方法,在计算三辊连轧管轧机轧制力各有所长,有限元方法计算精确,能够考虑多场耦合,可以用于验证计算和新品种开发,节省成本提高效率;数学公式法计算速度快,调整灵活,可用于快速计算和生产模型。

(3)两种方法都还存在不足的地方,都是比较理论性的计算,有限元模拟运算时间较长,数学公式计算做了等效简化,计算精度稍差,还需要加人更多的影响因素,并考虑不同工况下的情形,使计算结果与实际更接近,指导设备设计与轧制模型建立。