海洋内重力惯性波不稳定模态分析

邓冰，张翔，张铭

(1.北京应用气象研究所,北京100029；2.海军海洋水文气象中心,北京100079；3. 解放军理工大学气象海洋学院,江苏南京211101)

1 引言

海洋中的内重力惯性波是普遍存在的一种海洋内波，其对海洋的质量、动量和热量输送起着重要的作用；该内波也是海水运动的重要形态，会引起海水的内部混合,是形成海水温、盐微结构的重要原因[1]。本文对该海洋内波的不稳定模态进行分析；这不仅在海洋动力学研究中具有重要理论意义，而且对海洋资源开发和保护以及军事海洋保障中均有很大应用价值。

对海洋内重力惯性波的发生演变研究一直是物理海洋学的重点和热点，然而由于海洋内波现场观测资料获取困难以及流体动力方程组在数学上解析求解的限制，关于海洋内波生成机制至今尚在深入研究中。有很多因素都能激发海洋内波，它们可来自海面、海底和海水内部。例如海面风应力和海面气压场，上混合层中海水密度水平分布不均匀，潮流或海流流经凸凹不平的海底地形，海水内部背景流的水平切变和垂直切变等等。LUC RAINVILLE 等[2]对2000年4月中国海东部的黑潮海洋调查资料进行了分析，发现在黑潮中存在较强的连续切变层；另外又分析了日本九州黑潮附近2002年4月的ADCP 和CTD 连续30 h 现场观测资料，探测到在黑潮中心有一系列流的切变，并发现存在向上和向下传播的高频内波，他认为黑潮较强的切变是生成海洋内重力惯性波的重要因素。此外，司宗尚，范植松等[3]指出南黄海的内孤立波集中分布于南黄海的南部，而在其北部极少出现的主要原因是在南黄海的南部存在较强的背景斜压环流和很强的背景正压潮流，而在南黄海的北部这两种背景流都很弱。Xu等[4-5]研究了南海的内潮波，发现了以高模态为主的半日内潮的存在，并对南海高模态主导的内波做了全面深入分析。张远凌[6]利用澳大利亚西北陆架海域1992年2月至4月期间现场锚系实验观测获得的温度及海流计资料，分析了该地区内潮及内孤立波的主要特征，且得到该地区的流场随时间变化强烈，在垂直方向上具有较强的剪切。显然以上司宗尚等和张远凌所研究的海洋内波是非线性的（因其为孤立内波形态），但其来源仍涉及到海洋线性重力惯性波的失稳（因失稳造成其振幅随时间增长，最终非线性效应将起重要作用）。由此可见，海洋背景流的水平切变和垂直切变在海洋内波的生成和演变中起着关键作用。由于海洋中随机的无穷小扰动无处不在，这些无穷小扰动在海洋内重力惯性波不稳定的条件下，则会发展为小的线性海洋内重力惯性波，以后其振幅继续增大到一定阶段后，就必须考虑非线性的作用，此时会演变成孤立内波。这种由无穷小扰动发展到线性海洋内重力惯性波的过程，也即海洋内重力惯性波的不稳定，就是海洋内波生成机制的一种，当然这其中也包含演变。

在大气中基本气流（背景风场）的垂直切变会造成内重力惯性波的失稳早已为人所熟知[7]，而海洋与大气同属地球流体，有相似的控制方程组（但状态方程不同），故而海洋中的基本流（背景流）的切变应该也会造成海洋内部重力惯性波的失稳现象，而以上有的学者也指出，在海洋有的地方背景流剪切较强，是生成内波的重要因素[6]。为研究切变背景流对海洋内波不稳定的影响，本文提出了一个基于海洋动力学的线性海洋内重力惯性波失稳的数学模型，给出了对其数值求解的方案，并用以探讨沿垂直切变背景流传播的线性海洋内重力惯性波的不稳定性。

2 数学模型及求解方案

2.1 数学模型

本文研究海洋内波的控制方程采用无粘绝热的Boussinesq 方程组,仅考虑小振幅内波情况下，则可对其控制方程组进行线性化处理。在文献[8]中对方程的线性近似有详细阐述。最后得到如下海洋内波的控制方程组：

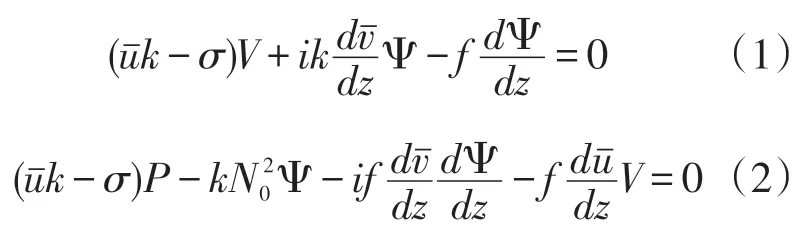
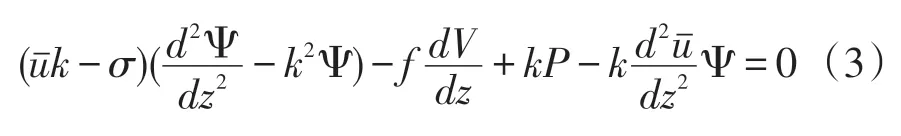
对海洋内波，海面可取刚盖近似，本文不考虑海底地形影响，这样上下边界条件可取为：

这里z=0 处为海底，z=H 处为海面，H 为海洋水深。这样方程组（1）与边界条件（2）则构成一个变系数复常微分方程组的特征值问题，在此σ 即为特征值，V,Ρ,Ψ 即为相应于该特征值的特征函数（特征波动）。虽地形影响是内重力惯性波的重要生成机制之一，但不是其唯一的生成机制；如上所述，背景流的垂直切变也是其生成机制之一，特别在大洋西边界流处，因该处流场垂直切变较强；而本文为突出后者，在此不考虑前者即地形作用。

2.2 数值求解方案

将整个水深区间[0,H]等距分为M 个子区间，即在垂直方向将水深分为M 层，以便对方程组（1）离散化。垂直方向采用交错网格，将Ψ 写在整数层网格点上，P、V 写在半数层网格点上。此时dΨ/dz 、dV/dz 和d2Ψ/dz2以及背景场的垂直切变均可用差分来近似表示，将也写在整数层和半数层的该网格点上；这样微分方程组（1）则可在垂直方向离散化后，转化为差分方 程 组。 令VM-1/2,PM-1/2)T，在此j=0 为海底，j=M 为海面，此时有Ψ0=0,ΨM=0。这样就可将该微分方程组的特征值问题离散化为复矩阵的广义特征值问题，也即有[6]：

3 内波的不稳定性

本文仅讨论沿背景流传播的内波不稳定性，即设内波水平传播方向与该背景流的方向相同，此时有，并取层结参数为常数和线性垂直切变背景流的情况，也即取和du¯/dz 为常数；之所以这样做是为了计算起来简单并便于与解析解进行比较，以便确定数值解的精度；同时这也大体不失一般性。计算表明，对同一波长L（波数k），可能有多个其虚部大于0的σ，而其特征函数（波动）的垂直结构也不同。即对同一内波波长其可有多个不同的不稳定垂直结构。本文以下主要讨论其增长率为最大者，并称其增长率为最大增长率；而相应的特征函数（波动）则称之为最大不稳定模态。

3.1 不稳定增长率随波长的分布

这里选取海表面背景流u¯ 的流速分别为0.5 m/s 和0.2 m/s，而海底则取u¯其值为0，水深取1000 m，此时该背景流的垂直切变分别为0.5×10-3s-1和 0.2×10-3s-1；其 他 参 数 则 取：=10-7s-2，f=10-4s-1，而内波波长L 的取值范围为：1 ＜L ＜600（单位km），由k=2π/L 则可得此时内波波数的取值范围。

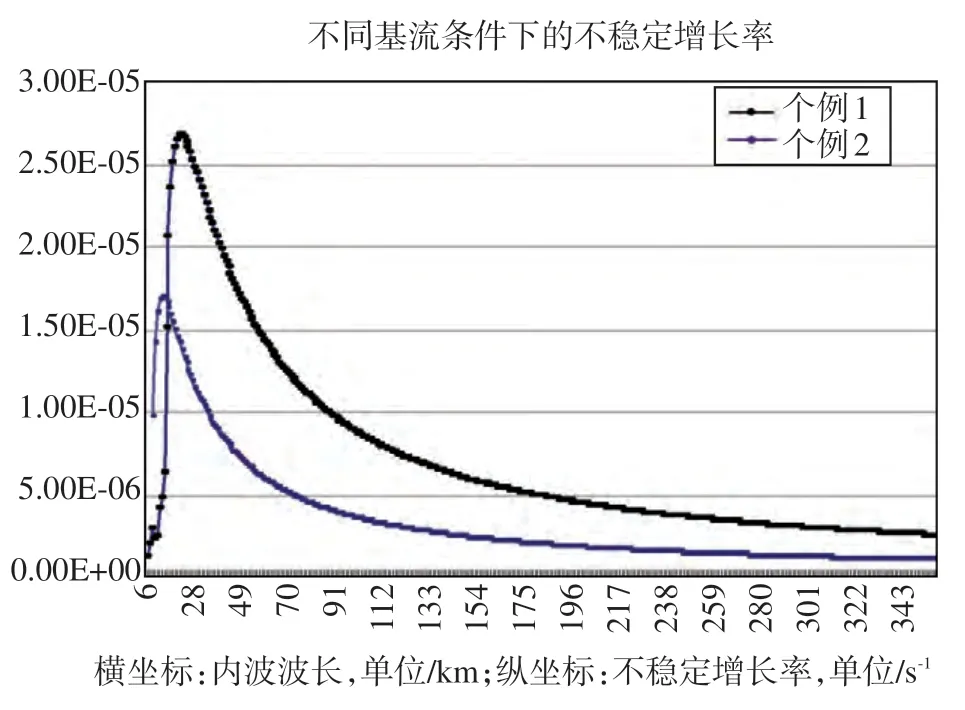
图1 不稳定增长率随波长变化

图1给出了海洋内波不稳定增长率与其波长的关系。图1中个例1、2分别为海表面流速为0.5 m/s和0.2 m/s的情况。在个例1中，对大于6 km 的波长则开始出现不稳定；在波长10 km到150 km 之间存在较大的不稳定增长率；最大不稳定增长率则出现在20 km的波长附近，其值约为2.7×10-5s-1，而其他波段的不稳定增长率较小；在小于20 km 的短波范围内该不稳定增长率增大最快（见图1）。

在个例2中，背景流的垂直切变变小，当波长大于10 km 时有不稳定发生，不稳定增长率的大值区仍在短波区域；不稳定增长率的最大值出现在波长约为14 km处，其值约为1.7×10-5s-1；该个例背景流的线性垂直切变要较个例1 小，不稳定增长率的最大值也比个例1 小，不稳定增长增长率随波长的分布态势则与个例1类似（见图1）。

图2 流函数不稳定结构

由上可见，在稳定层化海水中，背景流的垂直切变可导致短波长海洋内波的不稳定，该不稳定可存在短波截断。当背景流垂直切变减弱时，最不稳定海洋内波的波长也随之变短；这表明内波不稳定增长率对其波长具有选择性，其不稳定增长率在几十公里的短波段范围内占优，并受背景流垂直切变的制约。在其他海洋环境参数相同的条件下，背景流垂直切变则与最大不稳定增长率成正相关，即背景流垂直切变越大则其最大不稳定增长率也越大。

3.2 扰动不稳定的结构分析

这里采用个例1 的海洋环境条件，以分析内波波长为8、10、22和80 km时其最大不稳定模态的流函数结构。当内波波长分别为8 km、10 km、22 km和80 km 时，其最大不稳定增长率分别为1.19×10-6s-1、 2.87×10-6s-1、 2.67×10-5s-1和1.10×10-5s-1。其中在内波波长为22 km 时，在以上四者中，其不稳定的增长率最大。图2 给出了相应于以上四者的最大不稳定增长率流函数的垂直结构。由图可见，在内波波长为8 km 和10 km 时（见图2a,b），该流函数结构呈现正负相间的单圈环流，环流大体垂直，但在海洋内部的局部范围则会出现一处流函数的扭转。对8 km内波波长的流函数，虽其有扭转，但仅有一个流函数环流中心；当内波波长为10 km时，该流函数出现了上下两个环流中心，位于该流函数扭转处附近的上部环流中心范围较小，而位于下部的环流中心范围较大，两者构成“猫眼”结构。随着扰动波长的增加，流函数结构仍然为正负相交的单圈环流，但海洋内部流函数的扭转消失，出现了垂直方向略有倾斜的单圈环流（见图2c,d）。

图3 流函数不稳定结构

在内波波长分别为8 km、22 km、80 km 时只出现了一个不稳定模态，其即为最大不稳定模态；当内波波长为10 km时，不稳定模态增多，此时出现了4 个不稳定模态；最大不稳定模态的增长率上面已给出，为2.87×10-6s-1，相应流函数的结构也在图2b 中给出，其余3 个模态的不稳定增长率分别为2.08×10-6s-1、1.24×10-6s-1和1.055×10-6s-1。图3分别给出了其所对应流函数模态的垂直结构。由该图可见，次大不稳定增长率的流函数的垂直结构（见图3a）与最大不稳定增长率的结构（见图2b）相似，均呈现正负相间的单圈环流结构，流函数出现了上下两个环流中心，两者构成“猫眼”结构，只是其垂直方向配置与最大不稳定模态大致相反。对第3、4 个不稳定模态，其流函数结构则有明显的变化，此时在海洋内部上、下的局部范围则分别出现了流函数的扭转，即有两处流函数的扭转。此时流函数的大值中心分别出现在流函数扭转处附近（见图3b、c）。

综上可见，对内波波长8—80 km的最大不稳定海洋内波的流函数，其垂直方向的结构总体上表现为单圈环流；通常有一个环流中心，有时也出现两个环流中心，形成“猫眼”结构。对固定波长，当其最大不稳定模态的流函数出现“猫眼”结构时，则会出现多个不稳定模态，此时增长率最大的流函数模态其垂直结构最简单，而随着增长率的减小，相应流函数模态的垂直结构也越复杂。

方欣华[9]曾分析了海洋孤立波发生时的观测结果；他指出，孤立波的第一模态占优。张效谦[10]在南海北部陆坡，利用2000年8月—11月2 个半月的锚系定点观测资料，分析了南海北部陆坡海区内波的分布特征。他也指出，观测点的流动在大部分时刻均以第一模态的含能为主，该模态的水平动能所占的比例能达到总水平动能的70%—80%，但有时第二、三模态其含能也会明显增加。以上学者的分析表明，内波发生时其通常以第一模态占优，但某些情况下高模态也可能占优[4-5]；而本文则得到，具有最大不稳定增长率的内波其流函数的垂直结构最简单。虽然本文所讨论的在垂直切变背景流下失稳的内重力惯性波其条件与情况与他们所研究的内波不完全相同，但是两者仍有一致之处。

4 结语

由于海洋内波的特殊性，对其观测不仅难度较高，且耗资巨大；利用SAR 卫星虽具有同时获取大面积其海表特征的优点，但仅能获取大振幅内孤立波的海表特征，且受天气限制较大。当前无论是海洋工程上还是在军事应用均要求对海洋内波有更深刻的认识和研究，故本文的工作也成为研究内波失稳的一条途径。本文提出了一个基于海洋动力学的线性海洋内重力惯性波的数学模型，给出了对其数值求解的方法，并对沿垂直切变背景流传播的海洋内波的不稳定做了探讨，得到的结论有：

（1）在不考虑海底地形和采用刚盖近似的条件下，在稳定层化海水中，当不存在背景剪切流即背景流为常数时，则内重力惯性波均是稳定的；

（2）在较小的正层结参数下，即在较弱的稳定层化海水中，具有垂直切变的背景流会导致内重力惯性波的不稳定；

（3）不稳定内重力惯性波的增长率对其波长具有选择性并可有短波截断，而增长率最大处则出现在波长为几十公里的范围内；

（4）对固定的内重力惯性波波长，背景流垂直切变越强则其最大增长率越大。若此时有多个不稳定模态，则增长率最大的模态其垂直结构最简单；

（5）不稳定内重力惯性波流函数的结构在垂直方向大体呈单圈环流形态，环流中心可以是一个，也可以是2个，后者则呈“猫眼”结构。

本文为了凸现背景流对海洋内重力惯性波不稳定的影响，只分析了当背景流有垂直线性切变且层结参数为较小常数时，沿背景流传播的不稳定海洋内重力惯性波的增长率及其流函数的结构。在实际海洋中，背景流的变化和层结的变化都较这里要复杂，不过本文的结果也大体不失一般性。本文采用的方案也能用于这些复杂的情况。

[1]Luc R, Robert P. Observations of Energetic High-Wavenumber Internal Waves in the Kuroshio[J]. Journal of physical oceanography,2005,34:1495-1505.

[2]徐肇廷.海洋内波动力学[M].北京:科学出版社,1999.

[3]司宗尚,范植松,于万春,等.南黄海非线性内波的数值模拟研究(2)—内潮的非线性演变[J].中国海洋大学学报,2011,41(5):015-022.

[4]Xu Z,Yin B,Hou Y,et al.Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea[J]. J Geophys Res Oceans, 2013, doi: 10.1029/2012JC008212

[5]Xu Z,Yin B, Hou Y. Multimodal structure of the internal tides on the continental shelf of the northwestern South China Sea[J].Estuarine,Coastal and Shelf Science,2011,95(1):178-185.

[6]张远凌.内波数值模拟若干特性分析[D].青岛:中国海洋大学博士论文,2010.

[7]张铭,张立凤,安洁.大气波谱分析及其不稳定性（第一卷）[M].北京:气象出版社,2008.

[8]邓冰,张铭.海洋内部波动的波谱和谱函数I-数学模型和计算方法[J].水动力学研究与进展A辑,2006,21(2):259-266.

[9]方欣华,杜涛.海洋内波基础和中国海内波[M].青岛:中国海洋大学出版社,2005.

[10]张效谦.南海北部陆架陆坡区内波与混合研究[D].青岛:中国海洋大学硕士论文,2005.