基于BP神经网络的船舶航迹控制技术

郭文刚

(中国电子科技集团公司电子科学研究院，北京100041)

0 引 言

神经控制是基于人工神经网络控制的简称，是神经网络控制自动控制领域的前沿学科之一，是在20世纪80年代末期发展起来的。它是智能控制的一个新的分支，在复杂的不确定、非线性、不确知系统控制问题的解决方面开辟了新途径。神经网络控制是(人工)发展中的学科，也是神经网络理论与控制理论相结合的产物。它汇集了生物学、神经生理学、脑科学、遗传学、自动控制、计算机科学等学科的理论、技术及研究成果。神经网络控制属于智能控制系统。在控制领域，将具有学习能力的控制系统称为学习控制系统。神经控制属于学习控制，因此它是智能控制的一个分支。

1 神经网络及船舶航迹理论

1.1 神经网络

人工神经网络也简称为连接模型或称作神经网络，由大量生物神经元的处理单元互连并联而成，或者与生物神经细胞相类似的大量的人工神经单位互连组成，它是一种进行分布式并行信息处理的算法数学模型，人工神经网络是在现代认识科学和神经生物学对人类信息处理研究的基础上提出来的。这种网络通过调整内部大量节点之间相互连接的关系，依靠系统的复杂程度，从而达到处理信息的目的，具有仿真控制功能。

神经网络是由大量神经元相互连结组成，每个神经元基本单位的结构与功能比较简单，但神经元基本单位组合而成的神经网络系统非常复杂。神经网络系统能对信息进行大规模分布存储、并行处理，具有良好的容错性、自组织性和自适应性。同时，具有较强的学习、识别、联想、记忆等功能。神经网络具有逼近任意复杂的非线性函数的能力，这一能力已经被证明。因此，神经网络系统广泛应用于系统建模、优化、状态估计等方面。在未来，自适应控制与神经网络结合形成的神经自适应控制将有可能应用于强干扰、控制非线性、难建模系统等。

1.2 BP 神经网络

神经网络按照网络信息传递的方向可以分为反馈型网络和前向网络。误差反向传播神经网络简称BP 网络。BP 神经网络能学习和存贮大量的输入－输出模式映射关系，是一种单向传播的多层前向网络，在存储信息前无需事前揭示映射关系的数学方程。输入层、输出层、隐层构成BP 神经网络模型拓扑结构。广泛应用于自适应控制、图像处理、模式识别、优化计算、系统辨识、最优预测、函数拟合等等领域。图1 为BP 网络示意图。

图1 BP 神经网络的示意图Fig.1 Diagram of the BP neural network

正向传播和反向传播组成BP 神经网络的算法学习过程。在正向传播过程中，网络信息从输入层经过隐含层，逐层处理，最后传向输出层。在传输过程中，每层神经基本单位的状态只影响下一层基本单位的状态。如果在输出层不能得到期望的输出结果，那就转入反向传播，系统误差信号将沿原来的连接通路原路返回，并且修改各层神经元的权值，最大程度降低使误差信号。

如图1所示，BP 网络的结构图中有M 个输入节点，每个输入层节点的输入等于这个节点的输出。输出层隐含层有q 个神经元，有L 个输出的节点，Wki是隐含层和输出层间的连接权值，Wij是输入层和隐含层间的连接权值。前一层节点的输出的加权和是隐含层和输出层节点的输入的总数，节点的激发函数、和、输入信号和决定节点的激励程度。

设有N 个训练样本，假定样本p 的输入/输出模式对Xp和{dpk}进行网络训练，隐含层的第i 个神经元在p 作用下的输入为:

第i 个神经单位(神经元)的输出为:

其中是激发函数:

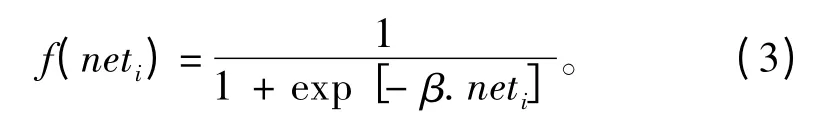
当β 的值趋于无穷时，激发函数趋于阶跃函数，设定β 的取值为1。将β=1 代入式(3)求导可得:

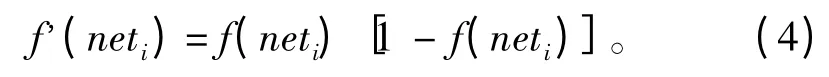
通过加权系数Wki，第i 个节点的输出向前传播到第k 神经元，并作为第k 神经元的输入之一，输出层的第k 个神经单位(神经元)的总输入个数为:

由此可知，输出层的第k 个神经单位(神经元)的总输出个数为:

如果给定模式的期望输出值dk 与神经基本单位的输出不一致，那么误差信号将沿着原路线从输出端反向传播，并且在传播过程中，神经元不断修正加权系数，使在输出结果最大可能的接近dk。对样本p 的加权系数的调整完成后，再送入下一个样本模式进行类似操作，直到完成N 个样本的训练为止。

1.3 船舶航迹控制发展现状

自动舵主要用于完成对航迹保持的控制、船舶航向、船舶航向保持等，它是船舶航向控制系统中最关键的控制设备。自动舵的研制主要经历以下4个发展阶段:

1)机械式自动舵

机械式自动舵具有比例控制功能，降低控制增益才能避免振荡。当船舶惯性很大时，比例控制的方法不能将船舶控制在制定航向上，且机械式自动舵燃料消耗高，因此，未被广泛应用。

2)PID 自动舵

PID 自动舵在船舶航向控制中，只要比例、微分和积分系数选择合适，就能实现良好的控制性能。PID 自动舵很大程度上提高了船舶的航向控制精度，并且，结构简单，参数调整方便，在当时得到了广泛应用。但它也存在不足，例如在大风浪中，转舵角较大会引起船舶偏航严重，非常危险。

3)自适应自动舵

随着自适应自动舵的发展成熟，自适应自动舵在船舶航向控制方面取得了突破性的进展。但是，自适应自动舵设计是建立在线性系统之上的，实际船舶运行是大干扰、实际船舶运行状态是非线性、大干扰的过程，因此自适应控制应用于船舶航迹控制的效果受到影响。

4)智能自动舵

智能自动舵采用知识表示、符号信息处理、启发式程序设计等相关技术对实际事件进行规划和决策，在实践过程中实现实际问题的求解。属智能控制技术包括神经网络、模糊原理等控制方法。

目前，国外已经将智能控制和船舶航向控制相结合。但是它仍然处于仿真实验阶段，还需要进一步研究才能运用于实际。

2 基于BP 神经网络的船舶航迹控原理

2.1 航迹控制方式

船舶航迹控制分为分离控制和综合控制。分离控制是间接式控制，综合控制是直接式控制。船舶航迹控制大体上可以分为3 个部分，如图2所示。

航迹控制根据船舶航迹可以分解为以下3 个问题:

1)船舶初始进入状态，即图2 中1－＞2 路线，此时航迹偏差较大，要求船舶快速返回航迹;

2)船舶在直线段航迹状态，即图2 中2－＞3路线，此时，船舶的航迹应按要求精度保持;

3)航迹转向点状态，即见图2 中3－＞路线位置，此时注意附近的转向问题。

根据船舶航迹控制原理，针对3 个问题的具体要求也不相同，具体如下:

当船舶初始进入状态，首先要确定航迹段，然后快速返回航迹，最后是跟踪航迹向;船舶在直线段航迹状态就要保持航迹;航迹转向点状态就要求船舶转向后，尽量减小航迹偏差的情况下，快速跟踪新航迹。

图2 航迹保持示意图Fig.2 Schematic diagram of track keeping

2.1.1 间接式航迹控制

间接式控制方案把控制分成互相嵌套的2 个环，如图3所示。

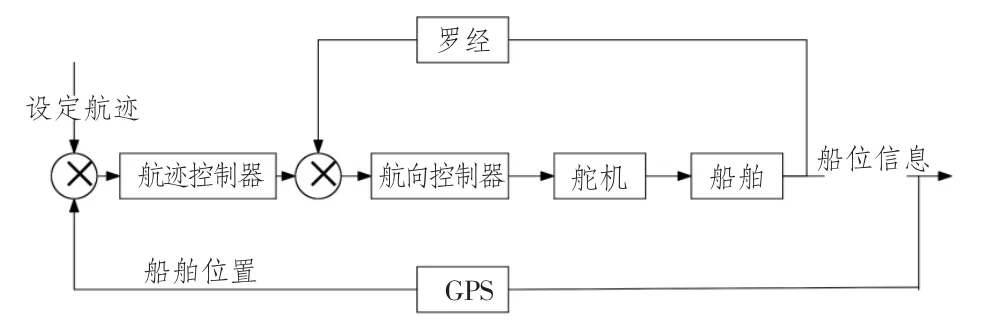
图3 间接式传播航迹控制原理图Fig.3 Indirect communication tracking control schematic

2.1.2 直接式航迹控制

直接式控制方案用于对船舶航迹进行高精度控制，此时，航迹控制器实际上是综合了分离控制方案中航向保持和航迹保持两部分的功能，如图4所示。

2.2 传播航迹误差计算方法

在船舶航行过程中，船舶航迹误差是船舶与船舶直线段航迹的垂直距离。航迹误差的计算对船舶航迹控制有重要意义。

已知设定(x1，y1)，(x2，y2)，(x3，y3)为航迹上的3 个位置点，在惯性坐标系下，假设船舶的位置为坐标(x1，y1)，船舶的航向角为ψ。

图4 直接式传播航迹控制原理图Fig.4 Schematic diagram of direct dissemination of track-keeping control

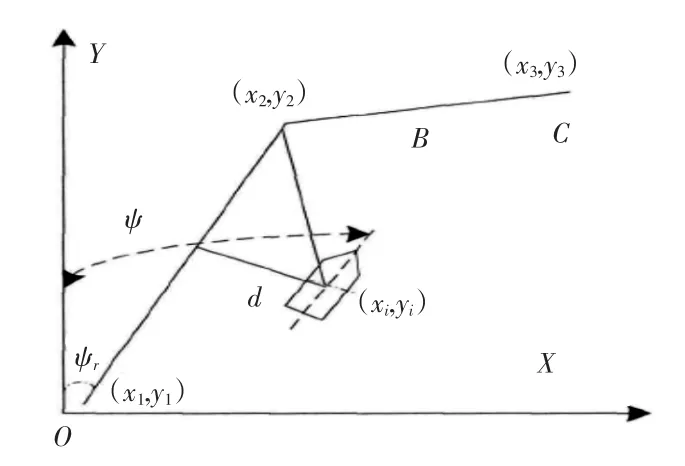
图5 航迹位置控制误差示意图Fig.5 Schematic diagram of track position control error

根据船舶的航迹误差算法可知，航迹直线段的距离为

期望航向角为:

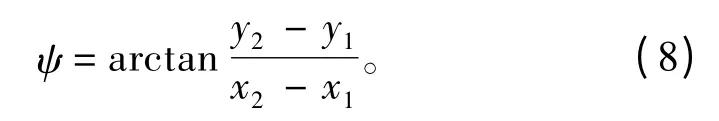
在惯性坐标系中，此航迹段的方程为:

根据点到直线距离定义及公式可以得到:

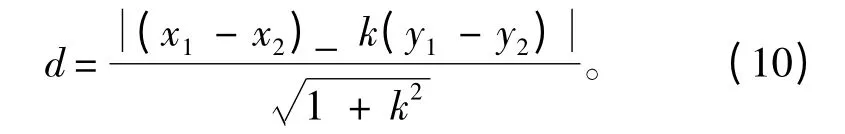
将式(1)、式(3)代入式(4)得到航迹的偏差为:

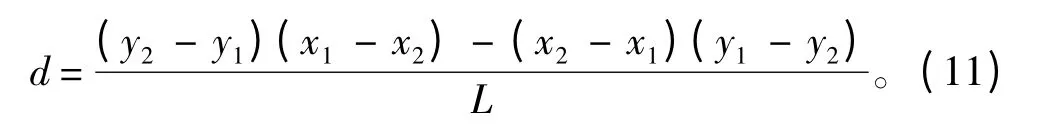
d(航迹偏差)的正负与船舶所在的位置有关，当d ＜0 时，船舶航迹段设定在左侧;当d ＞0 时，船舶航迹设定在右侧。在船舶航迹的间接式控制中，能够得到航迹偏差，就能得到航迹偏差引起的航正角Δθ，进而得到船舶航迹控制器输出的航向指令。

3 基于BP 神经网络的船舶航迹控实现

3.1 直接式航迹控制的实现

航迹直接控制中，传播航迹控制器是一个双输入、单输出的航迹控制器，输入量为航向偏差e=ψ1－ψ和航迹偏差d，输出量为命令舵角δ。2 个误差变量统一定义为E(t)，其值为:

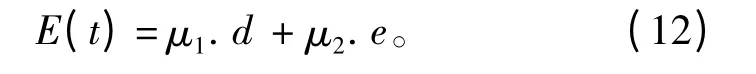
式中μ1，μ2为加权系数，μ1，μ2的大小根据船舶航迹控制的经验选取，选择PID 航迹控制器，得到舵角值为:

输出的命令舵角值为

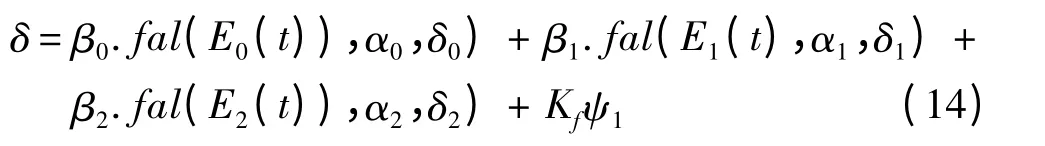
选定基于神经网络的非线性PID，设定初始控制参数为R1=100，R2=100，h0=4h，β0=14，β1=0.01，β2=20，αp=1.25，αi=0.45，αd=0.7，δ=0.1，Kf=0.5。

设定基于神经网络的常规PID 控制器的初始参数为Kp=22，Kl=0.001，KD=248。结果如图6 ～图11所示。

图6 静水条件下船舶航迹控制比较图Fig.6 Tracks under hydrostatic condition control comparison chart

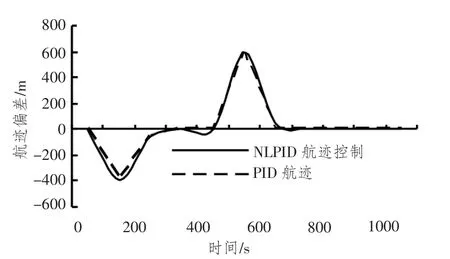
图7 静水条件下船舶航迹误差比较图Fig.7 Tracks errors under hydrostatic condition comparison chart

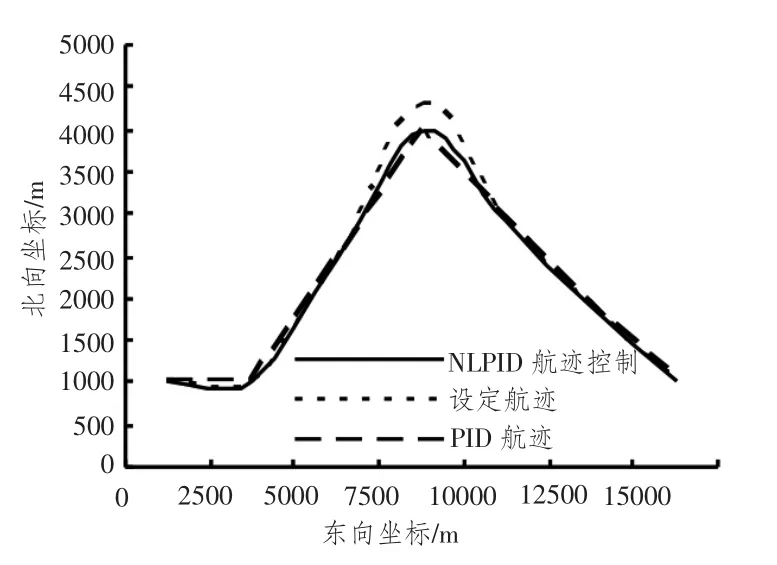
图8 四级海情下船舶航迹控制比较Fig.8 Four-tier ship track-keeping control under the sea

图9 四级海情下船舶航迹误差比较Fig.9 Four-tier ship track error under sea comparison chart

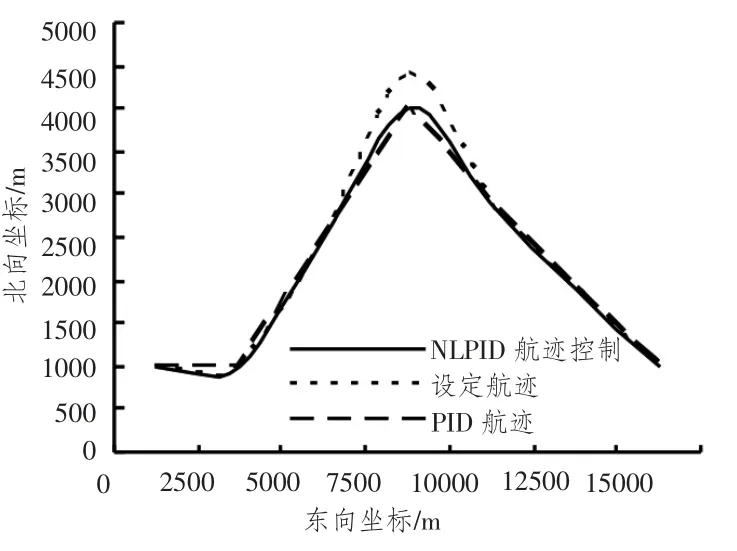
图10 六级海情下船舶航迹控制比较Fig.10 Six tracks under the sea control comparison chart

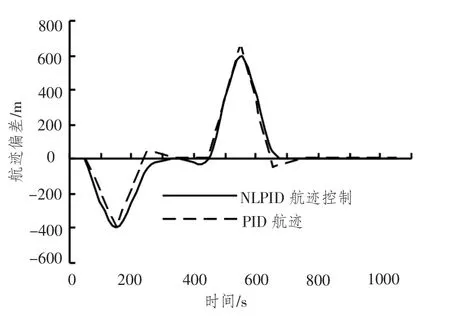
图11 六级海情下船舶航迹误差比较Fig.11 Six tracks under the sea errors comparison chart

图6 ～图11 表明，在静水条件下，基于BP 神经网络的自适应PID 与基于BP 神经网络的自适应非线性PID 控制器都能够很好的跟踪设定航迹，加上外部环境干扰，所以传统的船舶航迹偏差变得比较大，而基于BP 神经网络的自适应非线性PID 控制器能够使船舶航迹偏差消除快，舵角响应幅度小、速度快，操舵不频繁，机械损耗较小。同时，控制器具有前馈环节，能有效降低网络延迟对船舶航迹控制的影响。

3.2 间接式航迹控制的实现

在间接式船舶航迹控制中，以船舶航迹偏差d为输入是船舶航迹控制器，以航向指令ψ=ψr+Δθ为输出，ψr为船舶航迹期望航向，Δθ 为修正角，其值为k×d。修正角Δθ 使船舶航迹转向航迹设定的一边，船舶航迹偏差逐渐减小。航向偏差为e=ψr+Δθ－ψs，ψs为船舶的实际航向。非线性PID 控制器是基于船舶航迹误差的船舶航向控制器，以船舶的舵令为输出，船舶的航向偏差为输入。选定基于BP 神经网络的自适应非线性PID 控制器的初始控制参数为:

R1=100，R2=100，h0=4 h，β0=14，β1=0.01，β2=20，αp=1.25，αi=0.45，αd=0.7，δ=0.1，Kf=0.5。

选定BP 神经网络常规PID 控制器初始参数Kp=22，Kl=0.001，KD=248，结果如图12 ～图17所示。

图12 静水环境下船舶航迹控制比较Fig.12 Tracks under the water environment control comparison chart

图12 ～图17 可以看出，无论是静水还是在不同海洋情况下，本文选定的基于BP 神经网络的自适应非线性PID 控制器都能够使船舶快速的跟踪新航迹，甚至是在航运转向点处，舵角响应速度快，幅度较小，航迹偏差消除快，操舵不频繁，减少对舵机的消磨损耗，满足转向航迹段控制精度高的要求。同时，非线性PID 控制器具有前馈环节，能有效地降低网络延迟对控制性能的影响。采用基于BP神经网络的自适应非线性PID，比较船舶航迹的直接控制方式和间接控制方式，具体仿真比较结果如图18 ～图20所示。

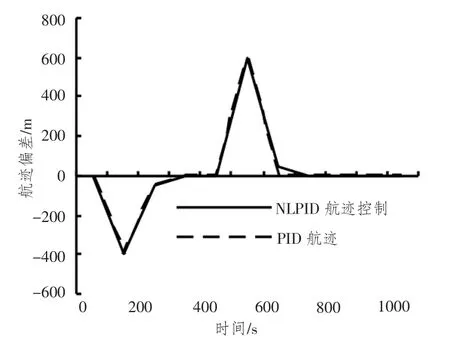
图13 静水条件下船舶航迹误差比较图Fig.13 Tracks under hydrostatic condition error comparison chart

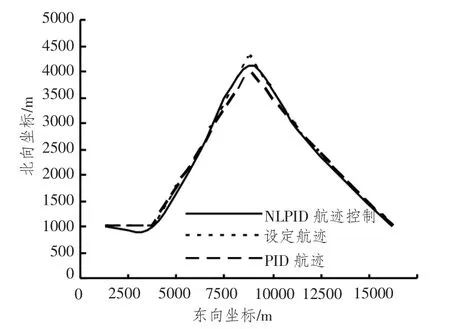
图14 四级海情下船舶航迹控制比较图Fig.14 Four-tier ship track-keeping control under the sea

图15 四级海情下船舶航迹误差比较图Fig.15 Four-tier ship track error under sea comparison chart

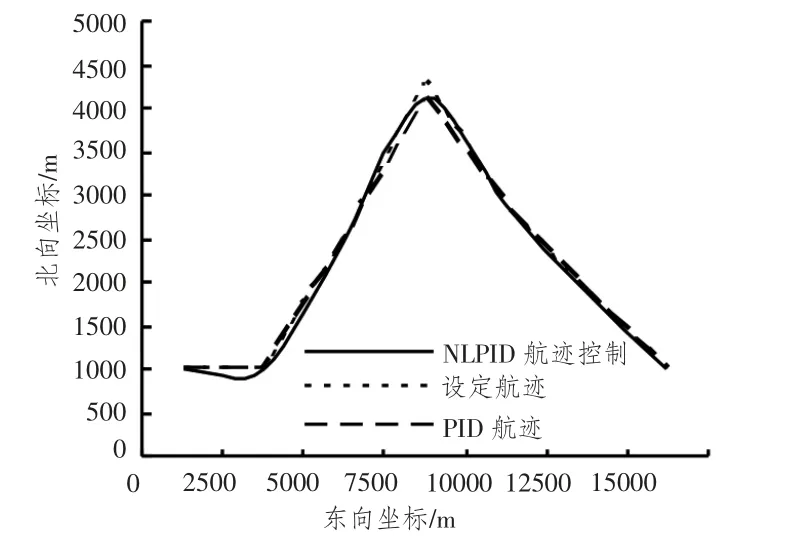
图16 六级海情下船舶航迹控制比较图Fig.16 Six tracks under the sea control comparison chart

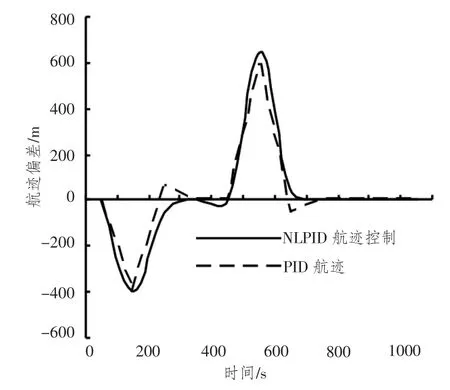
图17 六级海情下船舶航迹误差比较图Fig.17 Six tracks under the sea errors comparison chart

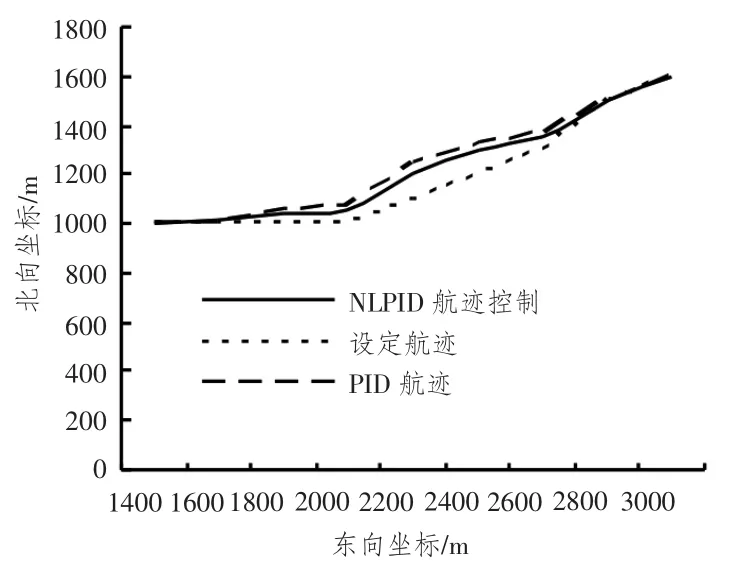
图18 转向处船舶航迹变化曲线Fig.18 Turning tracks changes

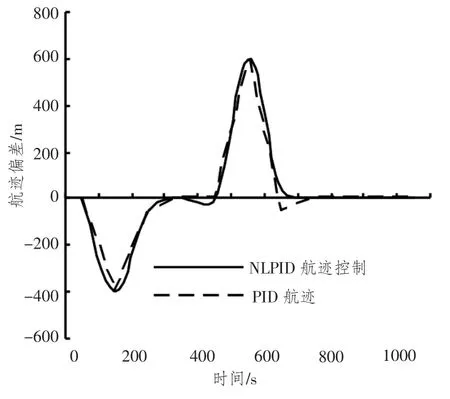
图19 航迹误差变化曲线Fig.19 Tracking error curve

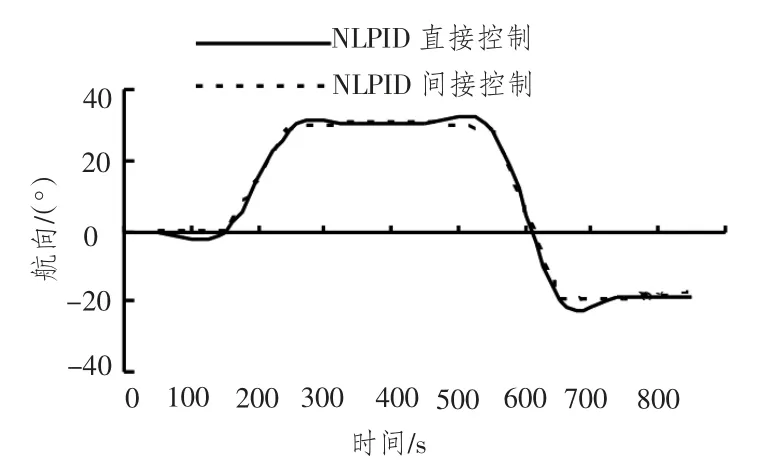
图20 船舶航向变化曲线Fig.20 Ship curves

从图18 ～图20 可以看出，间接式航线控制和直接式航线控制的跟踪设定航迹效果明显。从图中也可看出，直接控制方式比间接控制方式能够快速的跟踪新航迹，它转弯半径小，舵角响应速度快，航迹偏差消除快，舵机能耗小，操舵不频繁，控制精度高。

4 结 语

本文针对船舶在不同航速条件下航迹控制的问题，提出了一种基于BP 神经网络的控制算法，并通过仿真加以实现。文章首先阐述了网络神经、船舶航迹控制发展等相关问题的理论概述，为下文的研究奠定理论基础;然后详细基于BP 神经网络的船舶航迹控原理，包括船舶航迹控制方式、航迹误差计算方法等;最后，基于BP 神经网络的船舶航迹控的实现，主要从船舶航迹控制的2 种方式入手，对不同航海情况下船舶航迹控制情况进行比较，仿真设计，采用BP 神经网络计算，将实际的船舶视为非线性系统，利用神经网络的函数逼近特性实现控制器中非线性部分的在线估计。采用同时调整输入层－隐层、隐层－输出层间的权值阵的方法进行神经网络权值调整，最终实现船舶航迹控制技术。

［1］周涛．基于非线性PID 的船舶航向自动舵设计［J］．船电技术．2009，29(6):46－49．

ZHOU Tao．Ship steering autopilot design based on nonlinear PID［J］．Marine Technology，2009，29(6):46－49．

［2］孟浩．船舶航行的智能自适应控制研究［D］．哈尔滨:哈尔滨工程大学，2009:1－2．

MENG Hao．Research on the intelligent adaptive control for ship navigation［D］．Harbin:Harbin Engineering University PhD Thesis，2009:1－2．

［3］何玉彬，李新忠．神经网络控制技术及其应用［M］．北京:科学出版社，2010．

HE Yu-bin，LI Xin-zhong．Neural network control technology and its applications［M］．Beijing:Scientific Publishing Houses，2010．

［4］杨旭华．神经网络及其在控制中的应用研究［D］．杭州:浙江大学，2009:2－3．

YANG Xu-hua．Research on neural networks and its application in control［D］．Hangzhou:Zhejiang University PhD Thesis，2009:2－3．

［5］秦永祥．基于自适应神经模糊系统的船舶航向控制［D］．大连:大连海事大学，2010．

QIN Yong-xiang．Ship course control based on Adaptive neuro-fuzzy inference system［D］．Dalian:Dalian Maritime University Master Thesis，2010．

［6］罗四维．大规模人工神经网络理论基础［M］．北京:清华大学出版社，2009．

LUO Si-wei．Large-scale artificial neural network theories［M］．Beijing:Tsinghua University Press，2009．

［7］袁曾任．人工神经元网络及其应用［M］．北京:清华大学出版社，2009．

YUAN Zeng-ren．Artificial neural networks and its applications［M］．Beijing:Tsinghua University Press，2009．

［8］高雪鹏．BP 网络改进算法的性能对比的研究［J］．控制与决策，2011，16(2):167－171．

GAO Xue-peng．Research on improved BP network algorithm performance comparison［J］．Controlling and Decision Making，2011，16(2):167－171．

［9］曾军．神经网络PID 控制及Matlab 仿真［J］．现代电子技术，2008，27(2):51－52．

ZENG Jun．Neural network PID control and simulation of MATLAB［J］．Modern Electronic Technology，2008，27(2):51－52．

［10］谢立春．BP 神经网络算法的改进及收敛性分析［J］．计算机技术与自动化，2007，26(3):52－56．

XIE Li-chun．Improvement of BP neural network algorithm and its convergence analysis［J］．Computer Technology and Automation，2007，26(3):52－56．

［11］史春朝．基于改进BP 神经网络的PID 控制方法研究［J］．计算机仿真，2006，23(12):156－159．

SHI Chun-zhao．Study of PID control method based on improved BP neural networks［J］．Computer Simulation，2006，23(12):156－159．