独立学院数学改革之数学实验——Matlab 平台上“四步法”研究函数的单调性与凹凸性

刘亚轻LIU Ya-qing；沈大庆SHEN Da-qing

（北京工业大学耿丹学院，北京 101301）

（Gengdan Institute of Beijing University of Technology，Beijing 101301，China）

0 引言

高等数学是各高等院校的公共基础课程，根据非数学专业学生的特点，教学理念倾向于弱化繁琐的计算，注重数学的思想传授，侧重数学应用能力和创新能力的培养。而借助数学软件，使高等数学直观化，是高等数学改革的一个新动向[1]。Matlab 是一套功能强大的计算机数学软件系统，具有书写简单，内容丰富，功能强大，直观生动等特点。函数的单调性与凹凸性是高等数学中导数应用部分的一个重要内容，本文借助Matlab 软件，应用画图功能，给出了直观的研究函数图像性质的详细有效的求解步骤—四步法，该方法采用先求导函数零点再画图的顺序，能够准确，简捷地得出函数的单调性与凹凸性，且不容易丢掉极值点或拐点。

1 函数单调性、极值与凹凸性、拐点的判定

高等数学中导数的应用部分的一个主要内容是应用导数研究函数的单调性、极值与凹凸性、拐点，相应的判定定理有：

定理1：设f（x）在（a，b）内可导，如果在区间（a，b）内，有f′（x）>0，（f′（x）＜0），那么函数y=f（x）在区间（a，b）内单调递增（递减）。

定理2：设函数y=f（x）在（a，b）内具有二阶导数，如果在（a，b）内，f″（x）＞0，（f″（x）＜0）那么函数y=f（x）的曲线在（a，b）内是凹的（凸的）。

设函数f（x）在点x0附近有定义，如果对x0附近的所有的点，都有f（x）＜f（x0）（f（x）>f（x0））则称f（x0）是函数f（x）的一个极大（小）值，称x0函数f（x）的一个极大（小）值点。极大值与极小值统称为极值，极大值点与极小值点统称为极值点。连续曲线凹的曲线弧和凸的曲线弧的分界点叫做曲线的拐点。

2 Matlab 平台上“四步法”研究函数的单调性与凹凸性

Matlab 是一套强大的数学软件，具有高性能的数值分析和计算功能。借用Matlab 软件的画图功能，为直观、准确、迅速地研究出函数的单调性与凹凸性，提出“四步法”，即①求导；②求零点；③画图；④确定单调性或凹凸性。下面通过实例进行详细的说明。

例1：研究函数f（x）=2x3-9x2+12x-3 的单调区间与极值。

解：①求函数的一阶导函数。

②求一阶导函数的零点。

③做出原函数与导函数的图像。

fplot ('2*x^3-9*x^2+12*x-3',[0,3],'b-) %选定的作图区域（[0,3]）需包含一阶导函数的零点。

运行输出图1。

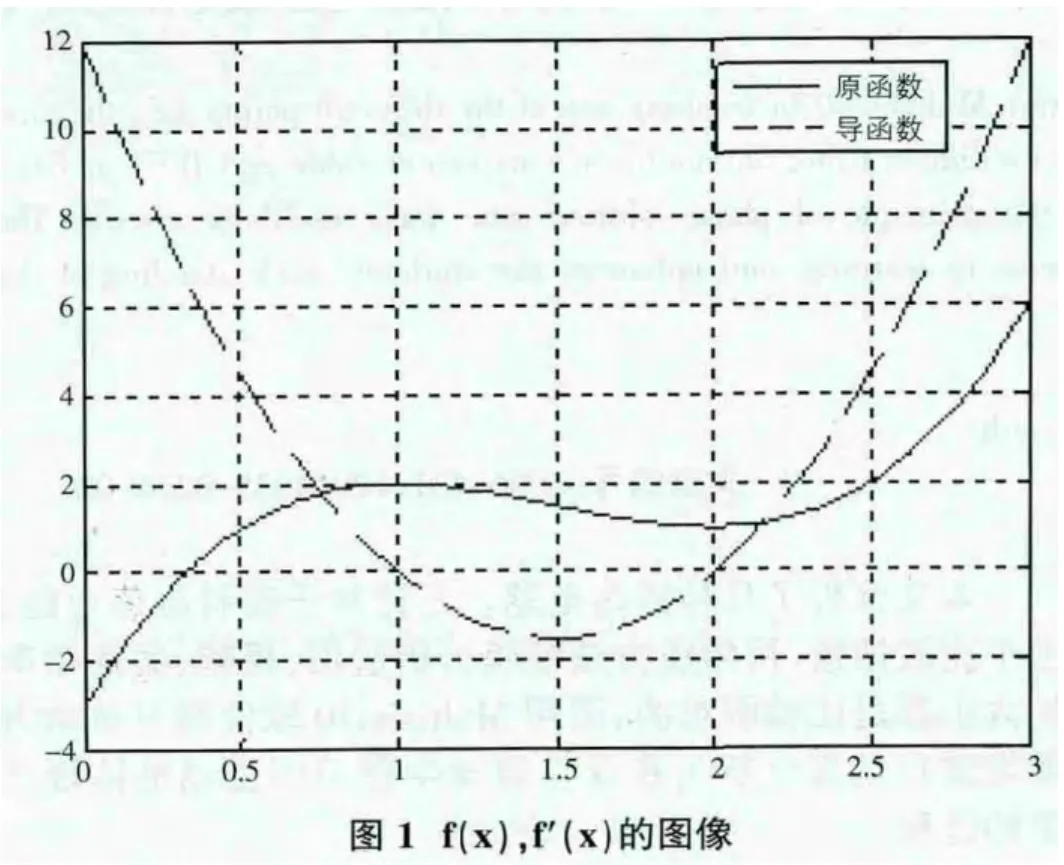
④确定函数的单调性与极值。

从图1 可以看出，函数f（x）在区间（-∞，1]，[2，+∞）单调递增，在区间[1，2]单调递减。极大值点xmax=1，极小值点xmin=2。

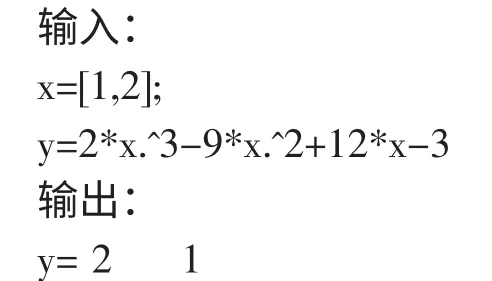
即极大值ymax=2，极小值ymin=1。

②求二阶导函数的零点。

f=inline(‘32/(1+2*x^2)^3*x^2-4/(1+2*x^2)^2’)；% 求一般函数的零点。

③做出原函数与二阶导函数的图像。

fplot ('1/(1+2*x^2)',[-1,1],'b-')%选定的作图区域（[-1,1]）需包含二阶导函数的零点。

运行输出图2。

④确定函数的凹凸性与拐点。

从图2 可以看出，函数f（x）在区间（-∞，-0.4082]，[0.4082，+∞）上是凹函数，在区间[-0.4082，0.4082]上是凸函数。拐点的横坐标为x=-0.4082 和x=0.4082。

即函数f（x）的拐点为（-0.4082,0.7500），（0.4082,0.7500）[2]。

3 结论

通过上面数学实验的实现，本文对应用Matlab 软件研究函数的单调性、极值与凹凸性、拐点给出了详细有效的步骤—四步法，不仅使学生对函数的特点有了直观的认识，对抽象的定理加深了理解与认识，而且弱化了高等数学中繁琐的数学计算，同时也使学生掌握了函数画图，求导，求多项式和一般方程的零点等数学运算的方法。本文巧用Matlab 软件研究高等数学问题，使数学问题变得通俗、直观、简单，该特点对于非数学专业的学生尤其明显，是顺应目前高校高等数学教学改革的一个有效途径。

[1]崔秋珍，李龙星，Matlab 平台上函数单调性与凹凸性判定的数学实验[J].河南：洛阳工业高等专科学校学报，2003，13（2）：46-47.

[2]章栋恩，马玉兰，等，Matlab 高等数学实验[M].北京：电子工业出版社，2008，11：50-55.

[3]丁永胜，李朝红.Mathcad 平台上函数间断点的数学实验[J].高师理科学刊，2001（03）.