基于MATLAB的工程项目管理多目标优化问题的解析求解及算法研究

薛亚宏，王加毅

（1.甘肃工业职业技术学院电信学院，甘肃 天水 741025；2.同济大学土木工程学院，上海 200092）

0 引言

工程项目管理以最低成本均衡资源，控制工程质量为目标，由工期子系统、费用子系统、质量子系统和资源控制子系统组成，从经济学角度来看，工程项目管理中进度目标、质量目标和环境保护目标的相互制约关系产生了多目标协同问题，即多目标优化。

“多目标优化”（Multiobjective Optimization Problem，MOP）是作为最优化的重要组成部分，它主要研究在某种意义下多个数值目标的同时最优化问题。在国防建设、工程设计、工程管理、数量经济学等领域都具有重要作用。近年来，传统多目标优化方法得到了很大发展，遗传算法、模糊优化、神经网络等现代技术也被应用到多目标优化中，使多目标优化方法取得很大进步。理论上，因素和指标考虑越全面对深入地研究问题越有价值，但这样会使问题变更为复杂和庞大，在条件允许的情况下，通常将目标减少到最少程度进行研究，即“单目标最优化问题”。尽管如此，多目标线性规划问题仍然是运筹学所面临的主要课题。

本文将从工程项目管理中所涉及的多目标优化问题的数学模型、无约束多目标函数的最小二乘求解、单目标转换、多目标优化问题的Pareto解集、极值问题、目标规划问题求解等方面进行基础性研究，并对每一种解析求解思路给出基于的算法设计。

1 多目标优化的数学模型

多目标优化问题的数学模型一般表示为

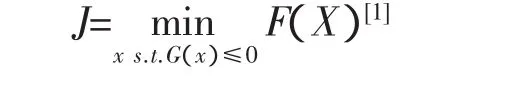
其中

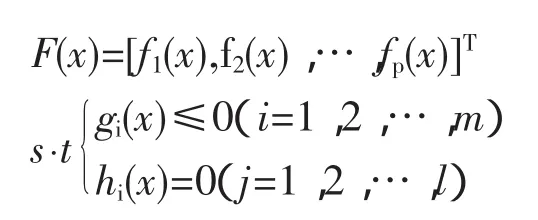
以上表示形式又称为多目标最优化问题的标准数学模型，下面将给出几种多目标最优化问题的求解途径及其算法实现。

2 无约束多目标函数的最小二乘求解

假设多目标规划问题的目标函数F(x)=[f1(x),f2(x),…，fp(x)]T，则可以按照以下方式将其转化为单目标问题

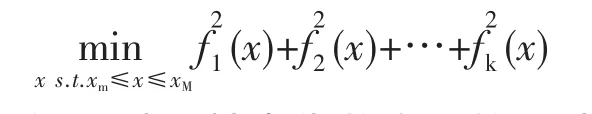
这样，便可以用基本代数方程的形式求解。在Matlab 中，调用 lsqnonlin（）函数

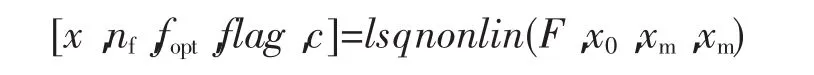
其中，F为给定目标函数写的M函数、匿名函数或inline（）函数，该函数为向量函数。x0为初始搜索点。最优化完成后，结果将在变量x中返回，其范数由nf返回。

如对如下无约束非线性多目标规划问题

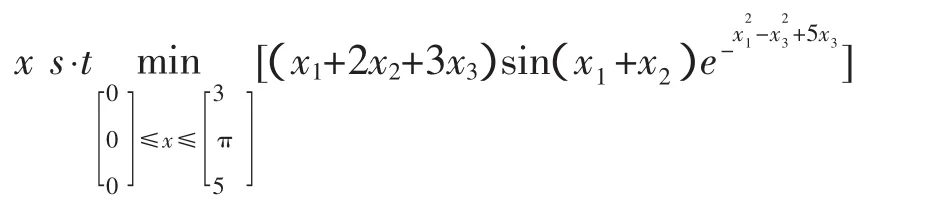
取 xm=[0；0；0]；xM[3，pi；5]；x=lsqnonlin（f，xm，xm），求最小值为 x=[3，3.1415，0]。

3 多目标问题转换为单目标问题求解

在多目标问题中，根据问题的实际情况，确定一个目标为主要目标，其余作为次要目标，并选取一定的界限值，即将其作为约束来处理，于是就将原多目标问题转化成一个在新的约束条件下，求主要目标的单目标最优化问题，如加权或最小二乘处理等。

3.1 线性加权变换及最小二乘解

对于一般多目标问题单目标化，最为常见的方法是对两个指标的侧重情况引入加权，使得目标函数改写成标量形式

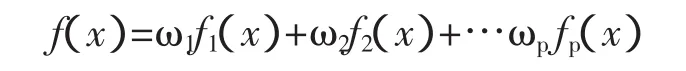
其中，ω1+ω+…ωp=1，且 0≤ω1，ω，…，ωp≤1[2]。对于这类加权变换后的目标函数使用linprog（ω1，ω2，…Aep，Bep，xm）进行优化，最终构造出不同加权系数下的最优化方案。

多目标线性规划问题的最小二乘表示

可由函数 zeros（d1，d2），Aep=[]；Bep[]；xm[]；xM=[]以及lsqlin（）直接得出。

3.2 一类线性规划问题的最佳妥协解

对于特殊线性规划问题

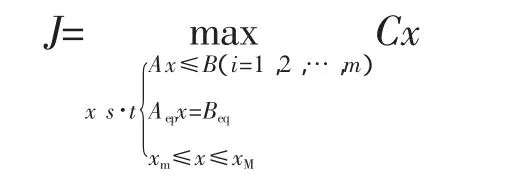
和传统线性规划问题不同，其目标函数是矩阵而非向量。每一个目标函数fi(x)=cix可以理解为第i方的利益分配[3]，所以这样的最优化问题可以认为是各方利益的最大分配。在约束条件的相互制约下，不可能每变量能真正最大化，此时各变量需作出适当妥协，得出唯一的最佳妥协解。其解析算法及程序实现如下：

①单独求解每个单目标函数的最优化问题，得出最优解 fk，k=1，2，…，p。

②通过规范化构造单独的目标函数

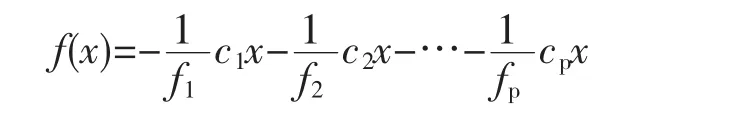
③应用单目标线性规划问题求最佳妥协解。根据以上算法，设计最佳妥协解的求解程序

4 多目标优化问题的求解Pareto解集

由于一般情况下多目标优化问题的解是不唯一的，其解可能随着决策倾向不同而不同。若重新考虑原始多目标优化问题，假设某一个目标函数分量取一系列离散点，则原来问题的目标函数的个数将减少，这样的处理将会产生新的解析结果[4]。

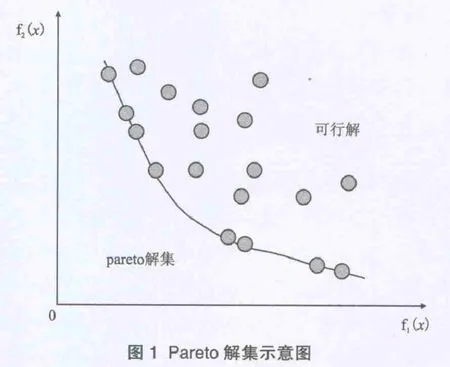
图1 Pareto解集示意图

考虑一个双目标函数的问题，可以先得出可行解的离散点，将这些点先在二维平面上显示出来（图 1）。

因为原始问题是求取两个坐标系 和 的最小值，所以可以从得出的可行解离散点提取出区域左下角的一条曲线，这条曲线就是原问题的解，称之为Pareto front解集[5]。主函数K=Pareto fron t([f1,f2,…,fp])的调用格式为

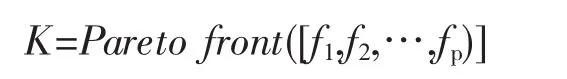
其中，M-为可行解离散点构成的列向量，K向量指示可行解离散点是否为Pareto解集中的点。

5 极大极小问题求解

多目标优化的一类重要问题是极大极小问题。假设某一组有p个目标函数fi(x)，对于各个目标的最大值，考虑进行最小化搜索，即。极大极小问题是在最不利的条件下寻找最优决策方案的有效方法。考虑到各类约束条件，极大极小问题可以改写成

使用fminimax（）函数求其最优解，调用格式为

本次调用格式接近于之前的fmincon（）函数，不同的是目标函数为向量形式描述。事实上，用匿名函数、inline（）函数和M-函数也可以作为新目标函数的一种表示形式，只是变量调用过程稍显复杂。

6 结语

在现实工程中，很多问题都是多目标优化问题，需要同时满足两个或者更多的目标要求，而且要同时满足的多个目标之间往往互相冲突、此消彼长。因此，在多目标优化问题中，不存在唯一的全局最优解，而是产生一组可选的折中的解集，由决策过程在可选解集中作出最终选择。文章在对最优化求解算法分析的基础上给出了每一类算法的实现，其它如分布估计算法、协同进化算法等新的范例也陆续被用于求解多目标优化问题。

[1]林锉云，董加礼.多目标优化的方法与理论[M].吉林：吉林教育出版社，1992：58-90.

[2]薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京：清华大学出版社，2002：201-215.

[3]魏静萱.解决单目标和多目标优化问题的进化算法[J].西安电子科技大学博士论文，2009.

[5]王雪松，郝名林，程玉虎.一种多目标优化问题的混合优化算法[J].系统仿真学报，2011，55（16）：15-21.

[5]刘仁云，张仪民，刘巧伶.基于多目标优化策略的结构可靠性稳健设计[J].应用力学学报，2012，40（02）：25-29.

[6]吴亮红，王耀南，袁小芳.多目标优化问题的差分进化算法研究[J].湖南大学学报（自然科学版），2012，53（02）：12-26.