高频振动压路机压实机理及参数选取探讨

2014-12-04庞瀛洲田建涛冉宝山

建筑机械化 2014年11期

庞瀛洲，田建涛，冉宝山

(长安大学道路施工技术与装备教育部重点试验室，陕西西安 710064)

压实方法可以分为静压、振动、揉搓和冲击这四类。最早期的压路机是人力或畜力牵引的光轮碾，19世纪的工业革命之后出现了蒸汽动力的自行式三轮压路机，1919年美国出现了以内燃机为动力的压路机，1930年德国人最先使用了振动压实技术，在20世纪80年代德国悍马（HAMM）公司又首先开发出振荡压路机，1999年日本酒井株式会社（Sakai）又开发出频率为4 000次/m in（约66.67Hz）高频振动压路机[1～2]。

高频振动压路机是随着压实技术不断发展产生的新型压实技术。

1 高频振动压实原理

1.1 振动机构振动及变幅原理

振动压路机振动轮由轮体、激振器和减震器3个主要部件构成，此外还包括传动轴、轴承和轴承座等。一般情况下，振动轴上装有2个固定偏心块，并横穿1个挡销，中间有1个空套的活动偏心块，振动轴支撑在2个调心滚子轴承上。振动马达输入动力驱动激振轴，激振轴带动偏向片产生离心力即为压路机的激振力。通过改变振动马达的转向，在挡销作用下固定偏心块和活动偏块产生2种不同组合来产生2组激振力和振幅，激振器的不同状态如图1所示。

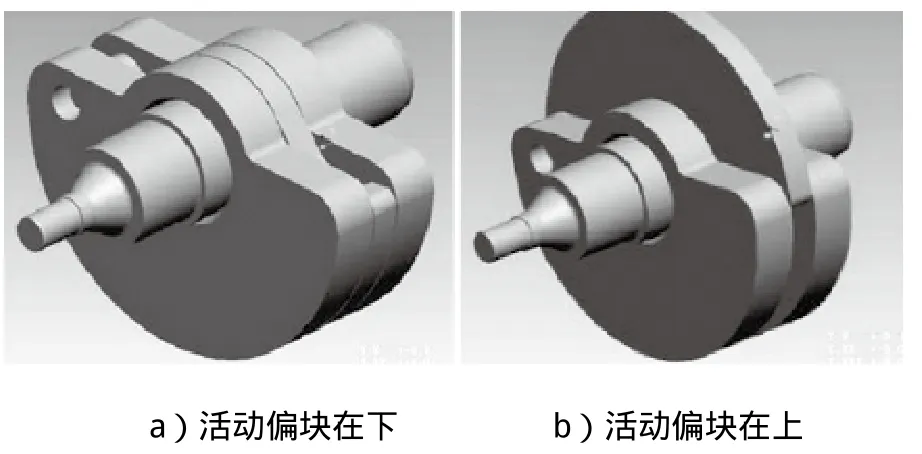
图1 振动机构示意图

在振动方向激振力F表达式如下式

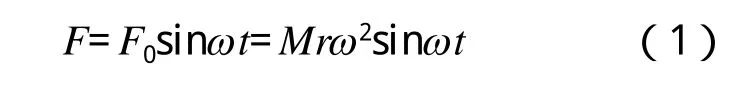
其中，M为偏心块偏心质量，r为偏心距；激振力F随时间变化规律如图2所示，为周期变化的正弦曲线。在高频振动下，压路机偏心块转速大于普通模式压路机的偏心块转速，反应在式(1)中则为ω较大。由式(1)可知，一方面，激振力F与ω的二次方成正比，ω增大使激振力F迅速增大；另一方面，ω增大代表着振动频率增大，即产生高频振动。

图2 振力F随时间变化规律

1.2 与作业介质相互作用原理

如图3所示，振动压实时，压路机钢轮产生的重力即静压力和振动产生的竖直方向的激振力作用于被压实材料。大颗粒材料由于质量大会得到较大的惯性力，它们将首先脱离周围材料向下运动，而小颗粒在大颗粒向下运动的同时，一方面在外力作用下也缓慢向下运动，另一方面在自身重力作用下填补大颗粒向下运动的空隙。这个过程中（图4）大小颗粒重新排列、相互“融合”，挤出水分和空气，与此同时，部分颗粒的棱角被磨掉，进一步加剧了密实过程。整个压实过程应在压实材料达到最大密实度以及大小颗粒排列均匀、相互填满空隙时结束。

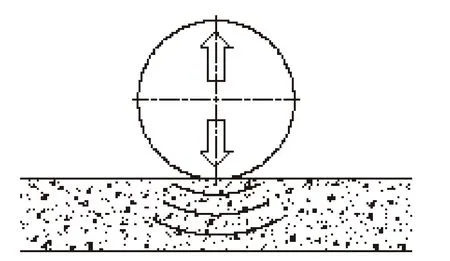
图3 振动钢轮与压实介质相互作用示意图

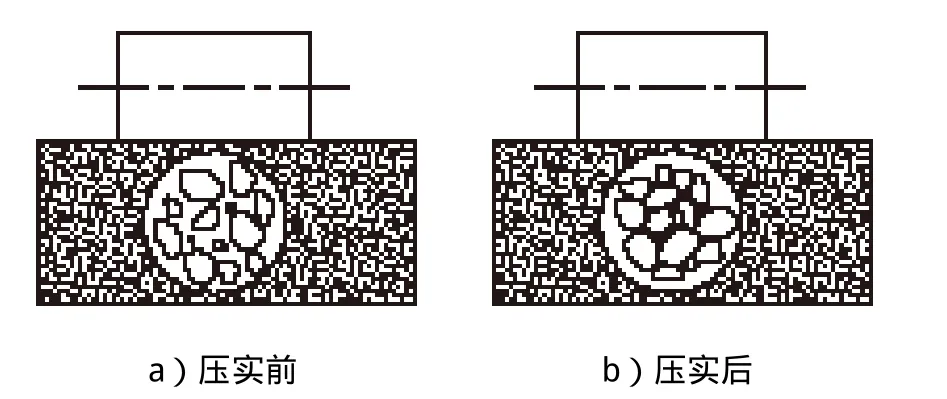
图4 实前后物料颗粒位置对比图

高频振动压实过程中，钢轮以大于3 600次/m in（60Hz）的频率快速、连续冲击待压实物料，使物理颗粒处于高频振动状态，根据“土壤液化学说”和“土壤共振学说”，此时物料颗粒间内摩擦力减小甚至丧失，在此状态下物料密实过程更容易进行；其次，颗粒棱角在高频振动和冲击作用下更容易被敲掉，也有利于密实过程；再次，高频振动对应更大的激振力，即钢轮对待压实物理的冲击力远远高于普通振动压路机；此外，振动频率越高，压实后路面平整度越好（图5)；与此同时，高频振动和桥梁的固有频率相差更大，对桥梁几乎没有影响，故高频振动压路机可以更安全地进行桥面压实施工。

图5 振动频率与平整度的关系

2 频率选取及振幅匹配

由表1可知，市场上的小吨位高频振动压路机多采用单一的高频低幅模式，大吨位的高频振动压路机多采用高频低幅+低频高幅模式。传统的双频率双振幅双钢轮振动压路机频率和振幅的组合难以适应各种复杂工况，而现行的高频双钢轮振动压路机则能够很好解决上述问题——工程实用性更强，施工效率更高。高频低幅工作模式，特别适用于薄层和桥梁面层压实，面层平整度好；低频高幅模式相当于传统的振动压路机，可用于厚层压实[3]。

衡量压路机压实效果的重要参数是压实度，故高频振动压路机频率的选取应该使得压实度最大。相关文献表明[4～5]，压实度与振动压路机的振动参数和工作参数有以下函数关系

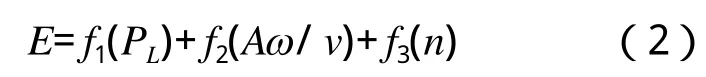
式中 E——压实度，%；

PL——振动压路机钢轮线载荷，N/cm；

A——振动压路机工作振幅，mm；

ω——振动压路机角频率，rad/s；

v——振动压路机工作速度，m/s；

n——碾压次数。

由式(2)可知：①当压路机的工作参数PL、v、n及振动参数A一定时，压实度E是振动参数ω的单值函数，故可通过试验找出压实度E与振动参数ω的关系，并绘制压实度E与振动频率ω的对应关系曲线图；②当压路机的工作参数PL、v及振动参数A一定，在振动参数ω取不同值时，压实度E是碾压次数n的单值函数，故可通过试验找出不同振动频率ω下，压实度E与碾压次数n的关系，并绘制不同振动频率ω下，压实度E与碾压次数n的对应关系曲线图。

图6所示为压实度与振动频率的对应关系曲线图，由图6可知：①压实度随着压实频率的升高先增大后减小；②当压实频率为70Hz左右时，对应的压实度最大。

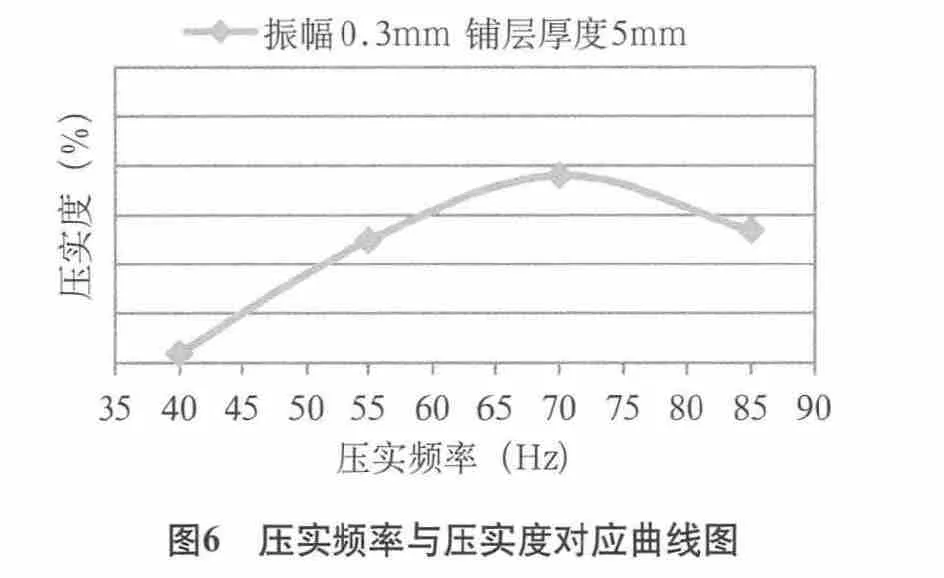
图6 压实频率与压实度对应曲线图

图7所示为70Hz和40Hz振动频率下，压实度与碾压次数的对应关系曲线图，由图7可知：①相同碾压次数下，70Hz对应的压实度大于40Hz对应的压实度；②40Hz碾压8次对应的最终压实度仅与70Hz碾压4次对应的压实度相当；③70Hz碾压8次对应的最终压实度远远大于40Hz碾压8次对应的最终压实度。

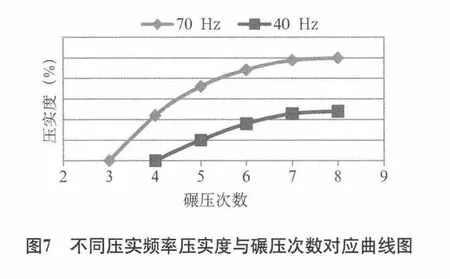
图7 不同压实频率压实度与碾压次数对应曲线图

综上所述，试验结果表明：高频振动压路机高频应该选取70Hz左右，此时对应的压实度值最大，即压实效果最好，通常情况下，高频一般取 67Hz或 70Hz。

将被压实材料视为弹性体，则振动压路机压实过程可视为该弹性体与压路机上、下车组成的一个共同的振动系统。建立振动压路机整机与作业介质组成的系统动力学模型如图8所示[6]，其运动学方程为

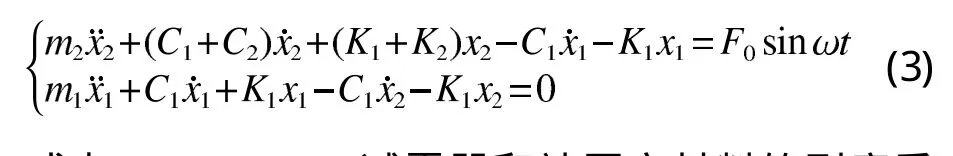
式中 K1、K2—— 减震器和被压实材料的刚度系

数N/mm；

C1、C2—— 减震器和被压实材料的阻尼系

数(Ns)/mm；

m1、m2——上车和下车质量；kg；

x1、x2—— 上车和下车的瞬时位移，mm；

ω、F0——激振力的角频率和幅值rad/s，N。

解微分方程(3)可得

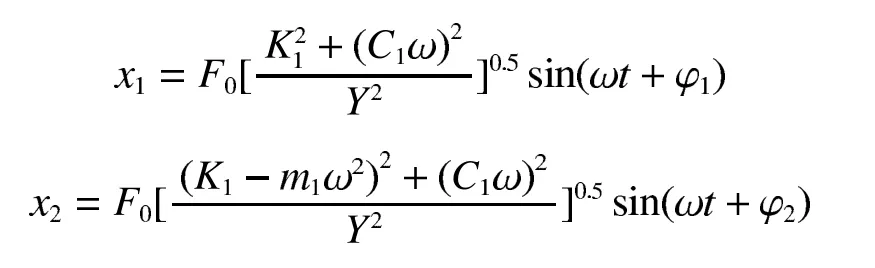
式中

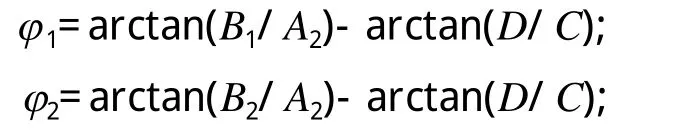
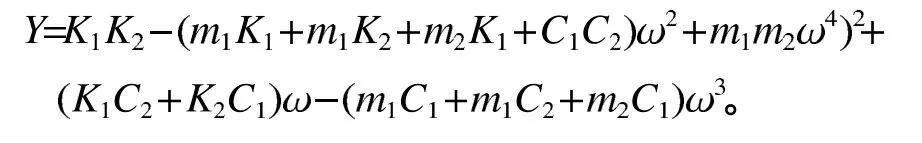
由微分方程的解可知压路机振幅的表达式为

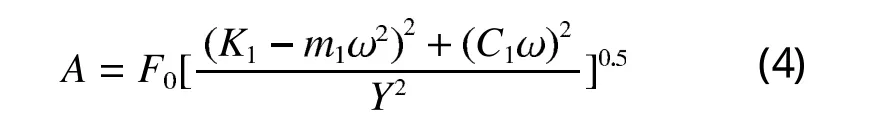
上述理论分析奠定了振幅选取的基础，但是通过计算机仿真技术得到的结论实际参考意义并不理想，故下面通过试验研究探讨振动压路机振幅A的选取的合理选取。试验采取“控制变量法”——在保持其他参数（包括压路机参数和介质参数）不变的情况下，只改变振幅来研究随着碾压次数的增加，振幅与压实度的关系。由于高频振动压力机适合压实面层，故以上层压实度为压实效果的衡量值。

试验结果统计如表2所示。根据表2可绘制各碾压次数下不同幅值下的上层压实度对比图(图9)。

表2 不同振幅对应上层压实度值

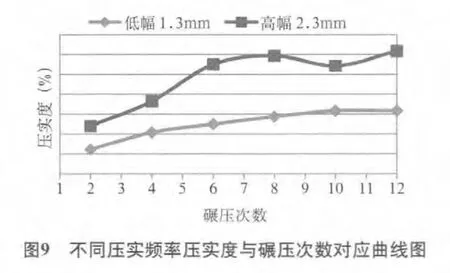
由图9可知：①相同碾压次数时，高幅对应的上层压实度值高；②随着碾压次数的增加，高幅对应的最终压实度大于低幅对应的最终压实度；③高幅时，随着碾压次数的增加当碾压次数大于8时，压实度反而降低，到12时又增大。

故根据试验结果可得出以下结论：①为取得较好压实效果，在振动压路机技术条件允许的情况下，振幅应取大值，但由于受到材料、轴承、减振等技术的制约，振幅的上限受到限制，现今市场上常见的产品振幅取值为0.3～0.4mm；②振幅取大值时应该对压路机压实度—碾压次数曲线进行测定，并根据测定结果制定合适的碾压工艺。