基于Matlab和Isight对发动机悬置元件优化结果的比较

张学萍，李 静

Zhang Xueping1，Li Jing2

（1.合肥工业大学 机械与汽车学院，安徽 合肥 230009；2.合肥工业大学 交通运输工程学院，安徽 合肥 230009）

0 引 言

随着人们生活水平的提高和汽车行业突飞猛进的发展，人们对汽车性能的要求也越来越高。在考虑汽车动力性、燃油经济性、制动性和操纵稳定性等性能的同时，乘车舒适性的需要更加倾向于对汽车行驶平顺性的考虑。发动机通过悬置元件安装在车身上，成为了汽车最大的振源，所以悬置元件应具有良好的隔振作用，尽可能降低发动机和汽车车架或车身之间的振动。

文中采用Matlab中的Pareto算法和Isight多目标优化法对发动机悬置元件的刚度分别进行优化分析，以某款客车为例，比较两种优化方案的解耦率，解耦率越高，优化方法越好。

1 Adams/View中建立模型及仿真分析结果

根据某款客车的发动机悬置系统的惯性参数和位置参数确立动力学模型，建立左右对称的 6自由度悬置系统，如图1。用Adams中的Vibration插件对模型前 6阶振动固有特性进行分析，结果如表1。

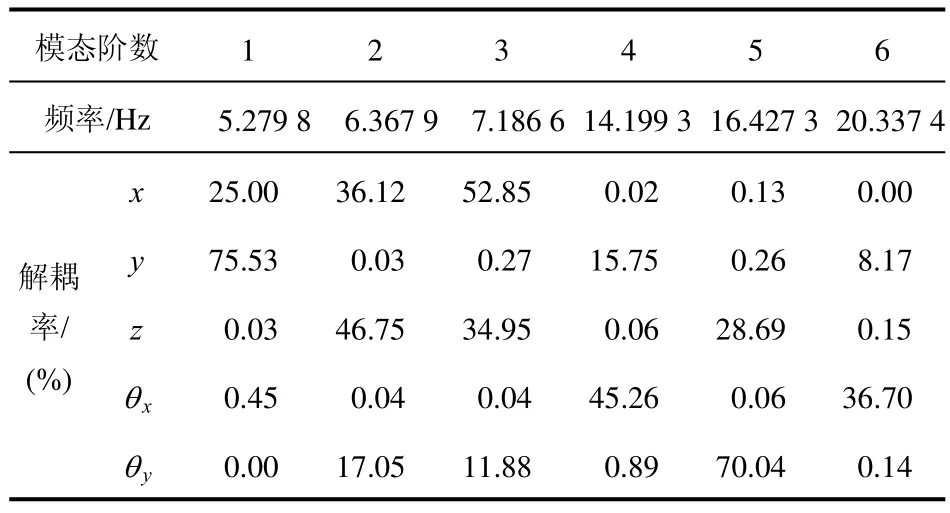
表1 优化前系统各阶固有频率和解耦率

θz23.78 0.02 0.01 38.67 0.83 54.16

文中研究的发动机是 4缸四冲程，根据隔振原理可知，此悬置系统的频率范围是 5≤f≤17.7 Hz。由表1看出悬置系统的最大振动频率过高，不利于隔振。解耦率的最大值为75.53%，其余5阶解耦率都低于75%，其中Z轴方向的平动和绕X轴的转动的解耦率只有46.75%和45.26%，耦合效果不好，为优化提供了依据。

2 基于 Matlab中的 Pareto遗传算法优化

2.1 设计变量

采用悬置元件的各向刚度为设计变量，悬置参数分布是左右对称的，所以左右悬置的各向刚度是相同的，则设计变量的个数为 6个，分别为前悬置的各向刚度u1、v1、w1，后悬置的各向刚度u2、v2、w2。

2.2 约束条件

1）频率约束：考虑避开路面不平的振动激励和怠速时的隔振，发动机悬置元件的频率范围为5≤f≤17.7 Hz。

2）刚度约束：采用普通的橡胶悬置，压剪刚度比值应在3～8之间才能满足材料的性能和工艺要求。

3）添加约束：利用惩罚函数，添加1个新的目标函数

其中，q1为频率约束的罚函数；q2为刚度约束的罚函数，其中

其中，λ1和λ2为常数，且λ1>λ2>1，w为固有频率，B1和B2为压剪比的上下限。

2.3 目标函数的建立

悬置系统优化的目标是使振动频率合理配置、解耦率值最大和振动传递率最小，三者综合考虑，得到较好的隔振效果。文中采用能量解耦法，由Adams分析可知，Z轴方向的平动和绕X轴方向的转动的耦合效果不好，所以要重点解除这两个方向的振动耦合。因此，建立目标函数

其中，Pz和Pθx分别为Z轴垂直方向和绕X轴旋转方向的能量解耦率。这是一个多目标优化问题，可以将多目标优化函数简化成含有权重的单目标优化问题，其单目标优化函数

其中，∂=0.5，为加权因子。

在Matlab中编写目标函数和约束函数的M文件，然后运行M文件，得出最优解，如表2。

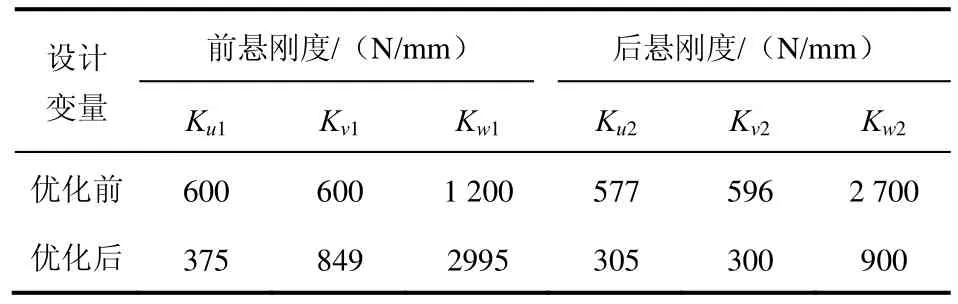
表2 Matlab优化前、后悬置刚度对比

表3 Matlab优化后系统各阶固有频率和解耦率

由表2、表3可以看出，一方面，优化后悬置系统的固有频率变为5.1178～15.9547 Hz，优化后的固有频率在频率约束的范围内；另一方面，重点考虑Z轴方向平动和绕X轴方向转动的解耦率也变为95.32%和97.00%，相对于优化前大大提高。总之，Matlab优化后的悬置刚度使隔振性能大大提高。

3 基于Isight优化

1）设计变量：设计变量的选取与Matlab中设计变量一样，只是在设定设计变量的变化范围时尽量选大一些。

2）约束条件：适当选取各个方向的固有振动频率作为约束，经过查阅资料可得固有频率参考范围如表4，而且相邻阶固有频率值的差应尽量大于1Hz，以免发生共振。

表4 各个方向固有振动频率参考范围

3）优化目标：选取各阶振动解耦率达到最大化，即x，y，z，θx，θy，θz解耦率值达到最大。

根据上述条件在Isight中设定好，然后运行，经过多次调节设计变量和约束条件的范围得到理想解，如表5所示。

表5 Isight优化前、后悬置刚度对比

表6 Isight优化后系统各阶固有频率和解耦率

由表5、表6可以看出，一方面，悬置系统的固有频率由原来的5.2798～20.3374 Hz变为优化后的5.1221～16.2601 Hz，优化后的固有频率在频率约束的范围内；另一方面，重点考虑的Z轴方向平动和绕X轴方向转动的解耦率也变为62.04%和55.77%，相对于优化前有所提高，但变化不大。

4 Adams/View中优化前、后动态响应分析

根据上文所述 Isight优化出的悬置刚度，其各阶振动的固有频率虽然满足了隔振要求，但其解耦率值明显低于Matlab优化后的解耦率值。比较两种方法的优化结果，最终选择优化效果好的悬置刚度值在 Adams/View中做动态响应分析，得出优化前、后右前和右后的悬置系统的 Z向支承响应。动态响应分析图如图 2和图 3可知。优化后的系统，Z轴方向的支承响应比优化前有了明显的降低。由此可以看出，采用Matlab优化的方案是可行的。

5 结 论

把Matlab优化结果和Isight优化结果作对比，可以看出两种优化方案都能使振动的固有频率满足隔振要求，优化后的解耦效果也比优化前有所提高。但比较两种方案的结果表明，Matlab优化后的解耦率远远大于 Isight优化后的解耦率，解耦效果更加明显，故选用 Matlab优化后的悬置刚度值。然后在Adams/View中建立模型并仿真分析，分析优化前、后悬置的振动情况，结果表明优化后的悬置系统提高了隔振效果，为发动机悬置系统的设计提供了参考。

[1]胡金芳，陈无畏，叶先军.计及弹性支撑的汽车动力总成悬置系统解耦研究[J].中国机械工程，2012，23（23）：2879-2885.

[2]熊伟.发动机悬置性能及优化研究[D]：重庆：重庆大学，2003.

[3]陈秋莲，王成栋.基于 MATLAB遗传算法工具箱的优化计算实现软件技术[J].现代电子技术，2007（2）：124-126.

[4]赖宇阳.Isight参数优化理论与实例讲解[M].北京：北京航空航天大学出版社，2012.