一类一阶微分方程的奇解

(怀化学院 数学系，湖南 怀化 418008)

1 引言

求一阶微分方程的奇解是非常困难的.文[1]给出了p-判别曲线法.先求出p-判别曲线，再验证所求曲线中的某一支是一阶微分方程的积分曲线.文[2]对形如

和

的方程研究了奇解存在的条件.文[3]得到了一阶常微分方程a(y)y'3-xy'+b(y)=0 有奇解的充分条件是2a(y)= a'(y)b(y)+2b'(y)a(y).本文进一步研究方程a(x)y'3-b(x)y'+c(y)=0的奇解存在的充分条件，进一步推广了文[3]的部分结果.

引理[1]对于一阶微分方程

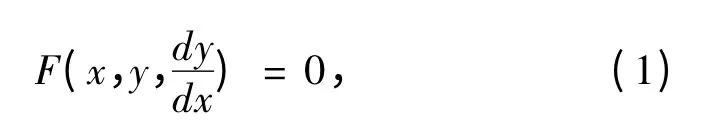
设函数F(x，y，p)对(x，y，p)∈G是二阶连续可微的.又设其p-判别式

(消去p后)得到的函数y =ψ(x)(x∈J)是微分方程(1)的解.而且设条件

以及F'p(x，ψ(x)，ψ'(x))=0 对x∈J成立.则y =ψ(x)是微分方程(1)的奇解.

下面用该定理研究微分方程a(x)y'3-b(x)y'+c(y)=0 存在奇解的充分条件，得到了以下结果.

2 主要结果

定理1 对于方程a(x)y'3-b(x)y'+c(y)=0，若函数a(x)，b(x)，c(y)在某个区间上满足

其中c'(y)≠0，则由方程0所确定的隐函数y =φ(x)是该一阶常微分方程的一个奇解.

证 由

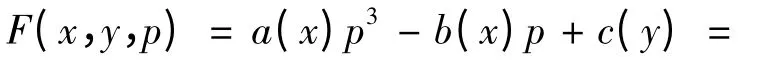
(2)-p(3)得-2a(x)p3+c(y)=0，则p3=代入(2)得

由(4)确定的函数记为y =φ(x).由(4)得，

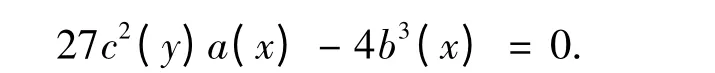
由隐函数存在定理，

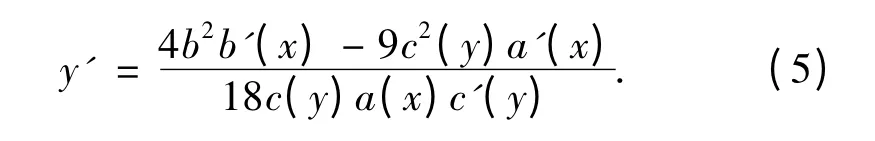
要使F'p(x，y，y')=0，即

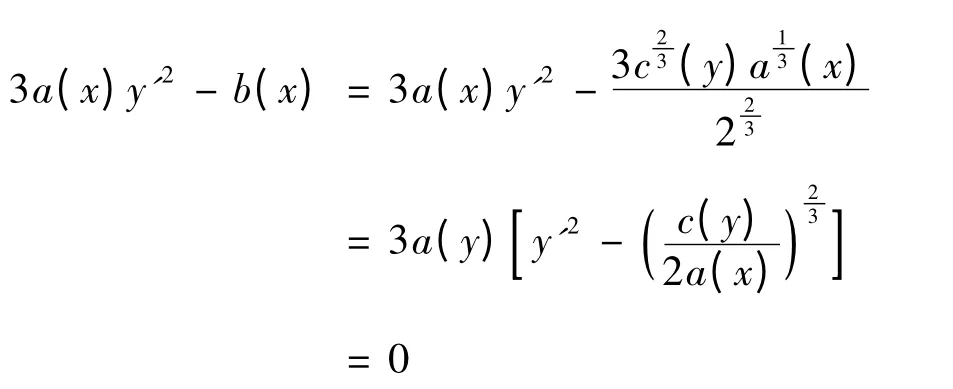
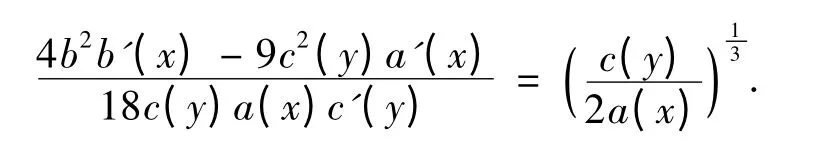
3 应用

例1 判断方程y'3-xy'+y =0是否有奇解.

解 由于a(x)=1，b(x)= x，c(y)= y，因此成立.奇解为所确定的隐函数即

[1]丁同仁，李承志.常微分方程教程(第二版)[M].北京:高等教育出版社，2004:109.

[2]何永葱.两类一阶常微分方程有奇解的条件[J].重庆教育学院学报，2007，20 (6):5-6.

[3]何永葱.一阶常微分方程的奇解的存在定理的应用[J].重庆教育学院学报，2009，22 (3):5-6.