具有初始相前曲率的光束在热非线性介质中的动力学研究
2014-12-03许飞张华峰韩立波长江大学物理与光电工程学院湖北荆州434023
许飞,张华峰,韩立波 (长江大学物理与光电工程学院,湖北 荆州434023)
近几年来,国内外的一些学者发现空间光孤子在全光控制、全光开关、光信息处理、光波导、光学互联器件等方面有着很大的应用价值,空间光孤子成为了光信息领域的研究热点之一。光束子的形成是介质的非线性引起的自聚焦效应和光束自身的衍射效应相互作用,达到平衡的结果。常见的能形成光孤子的介质有热非线性介质、向列液晶和非局域kerr介质等。特别值得注意的是,在热非线性介质中,发现了一些新奇的光学特性。Carmel Rotschild等通过实验发现,对于椭圆孤子来说,非线性折射率发生改变的区域远大于光束本身的分布区域,并且还指出孤子的形成显著受边界条件的影响,即使边界离中心很远[1]。文献 [2]研究发现,不对称的边界条件可以使孤子在传输过程中发生偏移和振荡,并得到了振荡轨迹和周期的解析解,而且发现振荡周期与入射功率、入射位置以及样品横截面的纵横比有关,这就为远距离地控制孤子提供了理论基础。另外,在时域中,光脉冲的初始啁啾会影响脉冲的传输,而在空域中,初始向前曲率(空间啁啾)会对光束产生什么影响鲜见报道。为此,笔者具体研究了具有初始向前曲率的光束在热非线性介质中的传输特性。
1 热非线性介质理论
在热非线性介质中,激光的热致非线性起主导作用,当光束进入介质时,由于介质可以吸收光的能量,而使自己成为一个热源,热源的扩散会引起温度在介质中的分布不均匀。温度的不均匀分布会导致介质折射率的改变。其温度用泊松方程[3]表示:

式中,k为热传导系数;a表示介质的热吸收率;T(x,z)表示介质中温度的分布函数;q(x,z)表示光场振幅包络;x表示横向坐标;z表示光束传播方向上坐标。笔者取k=a。
光束的传输用非线性薛定谔方程[4]描述:

式中,σ表示非线性调制系数。
令σ=1,则表示热非线性介质本身均匀分布的。方程(1)和方程(2)组成了光束在热非线性介质中传播理论的模型。
2 热非线性介质中的稳态解
光束在热非线性介质中的传输演化可以由方程(1)、(2)描述,边界条件为光束强度和温度在两端边界上的值均为0,即q|x=±L/2=0,T|x=±L/2=0,L为介质的宽度。笔者用LU分解和分布傅里叶方法[5]进行求解。
首先,对方程(2)用分布傅里叶方法,得到线性项和非线性项的迭代格式。在前h/2的步长只考虑线性项,用线性项迭代格式,计算q(x+h/2),在h/2处加入非线性项时先计算T,对方程(1)用LU分解的方法来求解T。
再用非线性项迭代格式重新计算加入非线性项后的q(x+h/2),然后在后h/2的步长上只考虑线性项,得到q(x+h),如此反复迭代,直到满足收敛条件。求解结果如图1所示。

图1 方程的稳态解(实线)和温度分布(虚线)
3 具有初始相前曲率的光束在热非线性介质中的传输特性
初始相前曲率也叫做空间啁啾,其物理本质是光束偏离束腰入射,就可能对光束的传输演化产生影响。文献 [6]讨论了在实验上如何得到各种初始相前曲率。
首先由方程(1)和(2)得到热非线性介质中的稳态解,然后利用相位打印技术给入射光束加入初始相前曲率:

式中,w(x)为前面求出的稳态解;B为初始相前曲率。
用数值模拟的方法可以得到具有初始相前曲率的光束在热非线性介质中的传输演化图和光束宽度随传播距离的变化规律。
从图2可以看出,加入初始相前曲率以后,光束的振幅会发生周期的扰动。由图3可以看出,当初始相前曲率为负时,即在束腰后入射,使光束在初始阶段的衍射作用大于自聚焦作用,导致在最初是展宽的(见图3(a));当初始相前曲率为正时,即在束腰前入射,使光束在初始阶段的自聚焦作用大于衍射作用,导致在最初是压缩的(见图3(b))。
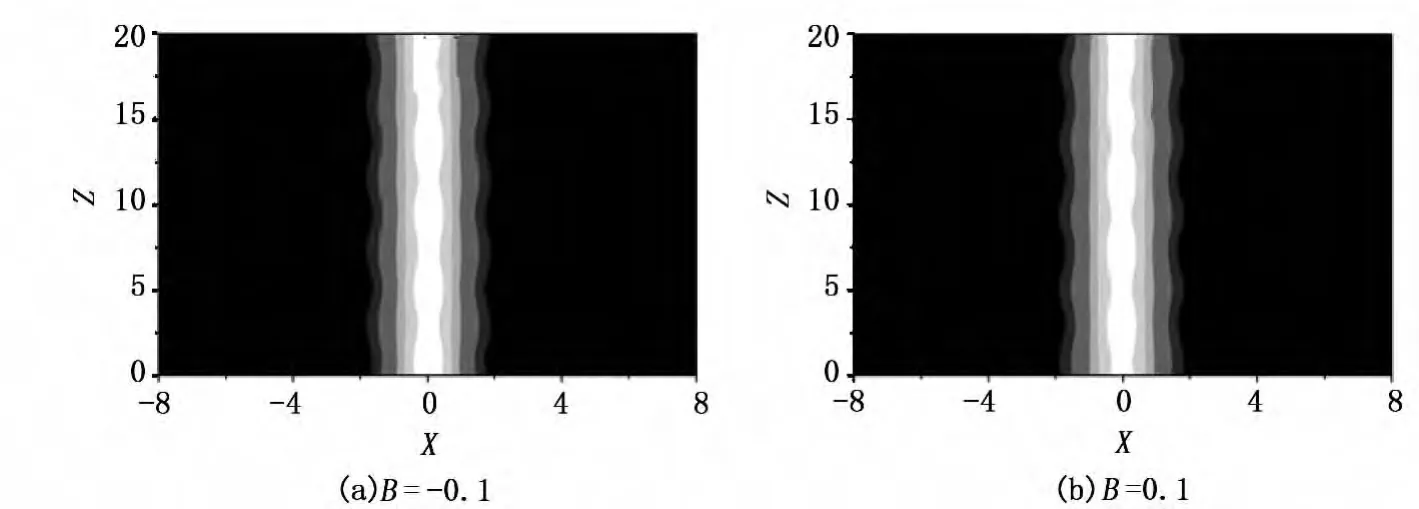
图2 带有初始相前曲率光束的传输演化图
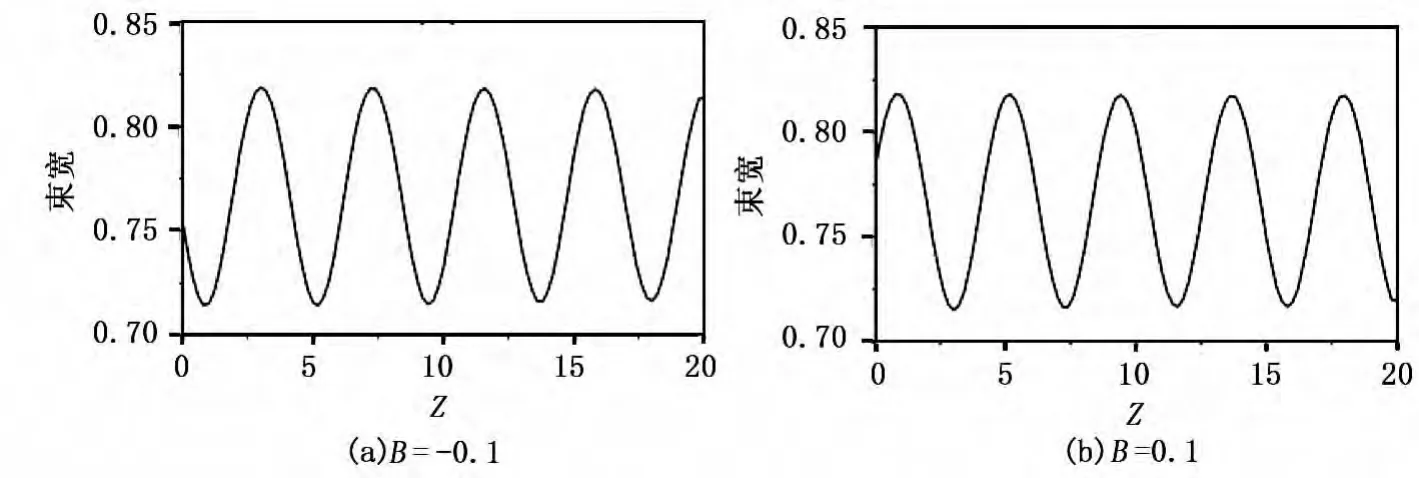
图3 光束宽度随传输距离的演化图
4 结语
用数值的方法研究了具有初始向前曲率的光束在热非线性介质中的传输特性。首先得到了在热非线性介质中的稳态解以及介质温度的分布;然后让稳态光束在介质中传输,通过数值计算发现,当初始相前曲率为负时,光束在开始的时候是展宽的,当初始相前曲率为正时,光束在开始的时候是压缩的,这个结果可能对于全光控制有一定的意义。
[1] Rotschild C,Cohen O,Manela O,et al.Solitons in Nonlinear Media with an Infinite Range of Nonlocality:First Observation of Coherent Elliptic Solitons and of Vortex-Ring Solitons[J].Phys Rev Lett,2005,95(21):213904.
[2] 梁炎斌,郑亚建,杨平保 .有界非局域非线性介质中空间光孤子传输的研究 [J].物理学报,2008,57(9):5690-5698.
[3] 曹雅平,黄春福 .非局域铅玻璃介质中偶极孤子解探究 [J].天津师范大学学报,2011,4(31):33-38.
[4] Dong L W,Ye F W.Stability of multipole-mode solitons in thermal nonlinear media[J].Phys Rev A,2010,81(1):013815.
[5] Govind P A.非线性光纤光学原理及应用 [M].第2版 .贾东方,余震虹译 .北京:电子工业出版社,2010.
[6] Guo Q,Xu C B.Influence of off-waist incidence on evolution of the Gaussian beam in the nonlocal nonlinear media[J] .Acta Phys Sin,2004,53(9):3025-3032.
