向量评估遗传算法优化聚乳酸载药微球工艺Δ

王婷，冯瑞梅，戴帅，仇丽霞（山西医科大学卫生统计教研室，太原030001）

在药物最优制备条件的多目标优化问题中，传统方法是将多目标问题转化为一个或一系列的单目标优化问题来解决，这样存在极大的主观性。通过这种方式得到的优化解，往往在某一个目标上是最优的，而在另一个目标上可能是较差的，不能保证所有目标都存在最优解，在实际应用中存在不合理的现象。实际上多目标的优化解不是唯一的，是将各个子目标进行协调权衡和折中处理，使各个子目标函数尽可能达到最优，是一组可供选择的、非受控的解方案集，称为Pareto非劣解集[1]。

向量评估遗传算法[2-5]（Vector evaluated genetic algorithm，VEGA）在解决均匀设计试验的多目标优化问题中，提供合理的Pareto非劣解集。VEGA是1985年由Schaffer提出的，其开创了多目标优化遗传算法的先河，利用内在并行的方式给出了多目标优化问题的Pareto非劣解集，解决了多目标优化的难题[5]。

聚乳酸（Polylactic acid or polylactide，PLA）的主要原料为速生资源玉米，经发酵制得乳酸，再以乳酸为主要原料而得到聚合物。其在人体内最终代谢为二氧化碳和水，是经美国FDA批准可用于人体的生物降解材料[6]。载药微球（Microspheres）是一种新型给药体系，粒径一般较小（1～250µm），其以高分子材料为载体，制成包裹药物的球形或类球形微粒，可以被细胞融合或被网状内皮系统内吞或被溶酶体中的酶降解后释放出药物[7]。聚乳酸载药微球具有良好的生物相容性、生物降解性、靶向性和控释性，在药学领域有着广阔的发展前景。本文将对聚乳酸载药微球的制备工艺用VEGA进行多目标优化，进而与原文献比较优化结果。前期本课题组已对VEGA进行了效果评价及程序测试，结果可靠，可用于实际问题的分析，为决策者提供选择的空间，达到节省人力、物力，降低研究成本的目的。

1 材料

1.1 仪器

UV2300紫外-可见分光光度计（上海天美科技有限公司）；IKA R20.DM型机械搅拌机（广州仪科设备有限公司）；KQ2200-E型超声分散机（江苏昆山市超声仪器有限公司）；LA-920激光粒度分析仪（日本Horiba公司）。

1.2 药品与试剂

线形聚d，l-乳酸（华南农业大学合成，相对分子质量：1.2×104）；二氯甲烷（广州化学试剂厂，分析纯）；亮蓝（英国Kris公司，分析纯）；PVA-224聚乙烯醇（日本Nopco公司，相对分子质量：6000，水解度：95%）。

2 方法与结果

2.1 两目标（药物包封率与平均粒径）的测定

聚乳酸载药微球用线形聚d，l-乳酸、二氯甲烷、聚乙烯醇等试剂合成，并通过一系列精密仪器测定其含量。以0.4%二氯甲烷的乙醇溶液为空白样，通过绘制标准曲线得出亮蓝的质量浓度（c）在1.0、1.5、2.0、5.0、7.5、10.0 µg/ml范围内与吸光度（A）的线性关系良好，相关系数达到0.9999。影响工艺制备的因素有内水相体积、二氯甲烷质量浓度、聚乙烯醇质量浓度、搅拌速度及氯化钠质量分数，评价工艺的指标有药物包封率（y1，%）和产物平均粒径（y2，µm）。进而确定目标值药物包封率与平均粒径的测定方法，按照以下公式进行计算。

载药量＝（微球中亮蓝的质量/微球的质量）×100%

包封率＝（微球中亮蓝的质量/所投亮蓝的质量）×100%

取适量的聚乳酸载药微球，用少量的注射用水分散后，用激光粒度分析仪即可测定载药微球的平均粒径。

2.2 试验设计及模型拟合

2.2.1 均匀设计试验。采用复乳法制备聚乳酸载药微球，影响工艺的因素有5个，即内水相体积（x1）、二氯甲烷质量浓度（x2）、聚乙烯醇质量浓度（x3）、搅拌速度（x4）及氯化钠质量分数（x5），每个因素各有8个水平，按均匀设计试验U8（85）进行8次试验，评价工艺的指标有包封率和平均粒径，试验结果见表1[8]。

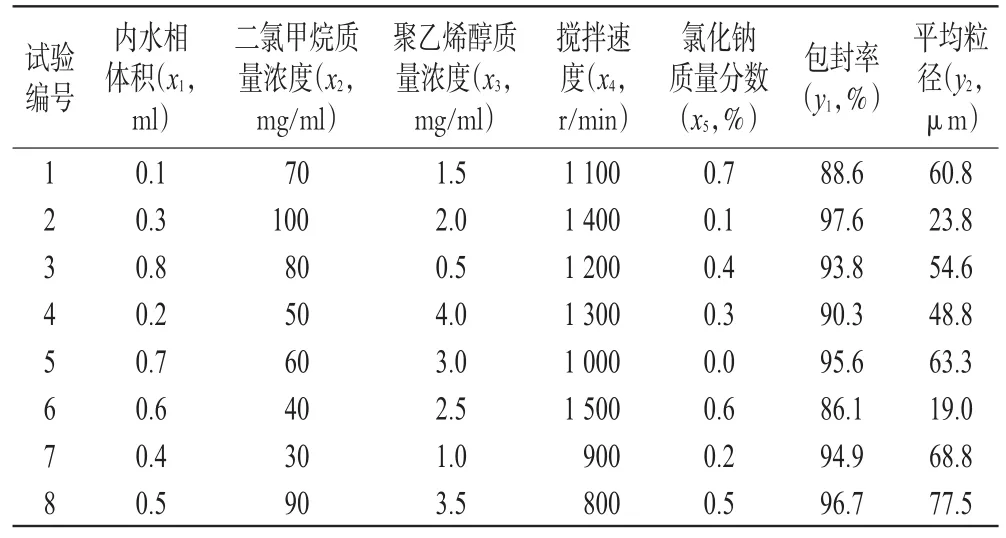
表1 复乳法制备聚乳酸载药微球均匀设计试验U8（85）结果Tab 1Results of uniform design U8（85）of Polylactic acid-loaded microspheres prepared by W/O/W emulsion

由表1可见，2号方案包封率最大，6号方案平均粒径最小，两个最优目标不在同一个方案中，于是将8次试验结果根据建立的二次回归模型中一次项、二次项的符号，得出最优制备工艺为较高的二氯甲烷质量浓度、较高的搅拌速度及较低的氯化钠质量分数，但并未给出具体解集。

2.2.2 模型拟合。文献数据采用逐步回归方法筛选变量，并对两目标（包封率与平均粒径）分别建立了二次型回归模型[8]。以包封率和平均粒径作为评价指标，得到与x2、x4、x5的回归模型。

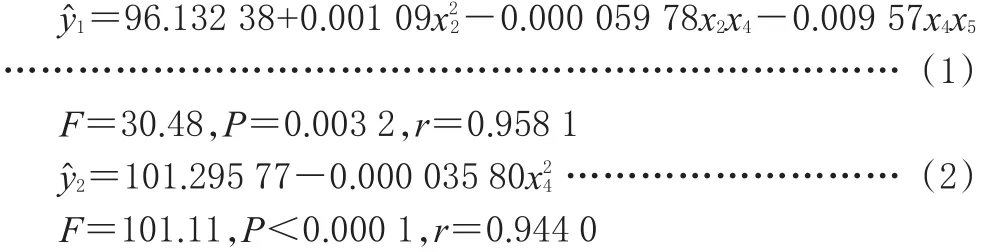
从公式（1）、（2）可知，两个目标值与因素之间拟合出的模型效果均良好，遗传算法可利用此模型进行两个目标值的优化分析。

2.3 单目标及多目标遗传算法的参数设置

分别以y1和y2为目标函数，用单目标遗传算法分别搜索药物包封率最大值的工艺条件及产物平均粒径最小值的工艺条件：初始种群为30、单点交叉概率为0.9、单点变异概率为0.01、最大进化代数为100，分别进行10次随机搜索。用VEGA进行两目标优化，参数设置同单目标优化，进行12次随机搜索。

2.4 软件及统计方法

利用课题组编写的Matlab 2009a外挂SGALAB工具箱Beta 5008完成遗传算法寻优，需设置参数和方程，在Current directory窗口中，Input text处设置参数，设置参数有最大进化代数、初始种群、单点交叉概率、单点变异概率，在SGA.FITNESS.MO_function.m处设置方程，再打开遗传算法程序SGALAB_demo_MO_VEGA.点击运行键开始运行程序，即可得出适应度曲线图与一组Pareto非劣解集。用SPSS 17.0软件进行统计分析，对运行VEGA得到的Pareto非劣解集及目标函数值用中位数、四分位数间距来描述。

2.5 模型转化

由于目标值产物y2要求得到最小值，而VEGA搜索得到的结果均为最大值，所以需将y2的模型进行转换，y2′即为y2的最大转化值，公式如下：

由公式（3）可知，用VEGA求得的最大转化值y2′通过模型转化即可求出y2的最小值y2。

2.6 VEGA搜索两目标Pareto非劣解方案

以y1和y2作为两个目标函数值，采用VEGA进行两目标优化分析，以达到y1最大、y2最小的目的。从回归模型公式（1）与（2）可看出，进入模型的因素有二氯甲烷x2、x4及x5，则VEGA搜索的因素也只有3个因素，结果详见表2。

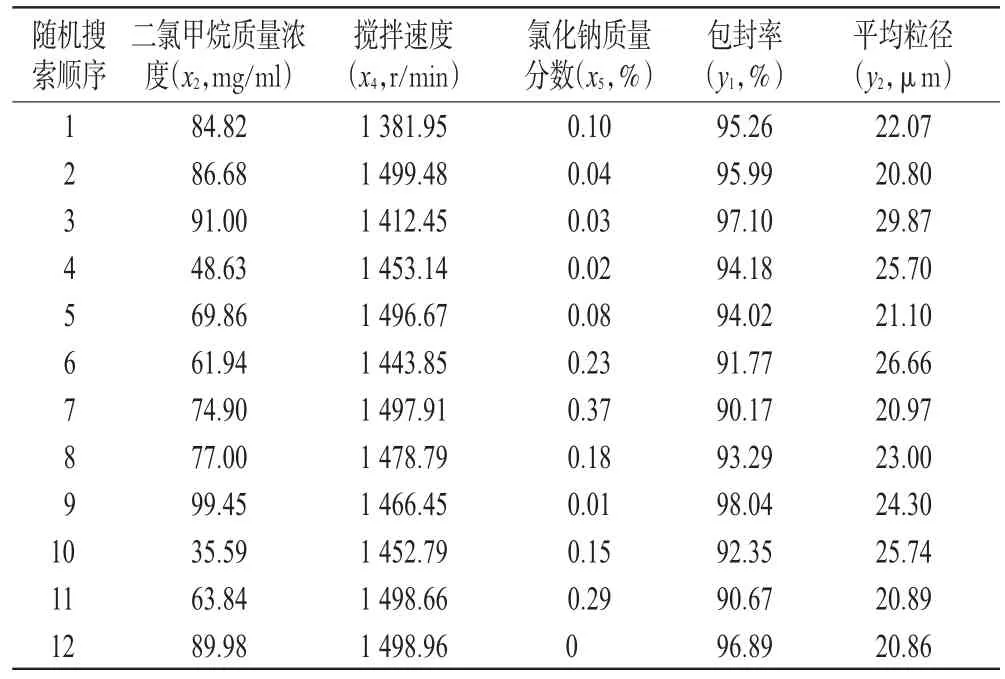
表2 VEGA两目标随机搜索结果Tab 2 Randomized search results of two-objective by VEGA

从表2可知，第2号与第12号试验搜索的两目标结果均较优，具有较大的包封率和较小的平均粒径，VEGA两目标随机搜索聚乳酸载药微球最优制备工艺即：2号试验x2为86.68 mg/ml，x4为1499.48 r/min，x5为0.04%，y1最大达到 95.99%，y2最小达到20.80µm；也可选择12号试验工艺，即x2为89.98 mg/ml，x4为1498.96 r/min，x5为0，y1最大达到96.89%，y2最小达到20.86µm。可根据试验的具体条件来选择不同工艺。

两目标最大适应度曲线见图1，平均适应度曲线见图2。

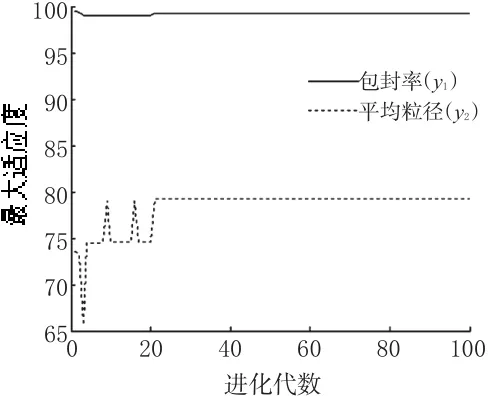
图1 两目标最大适应度曲线Fig 1 Two-objective maximum fitness-generation

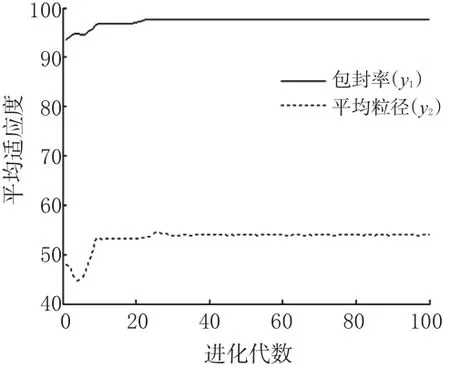
图2 两目标平均适应度曲线Fig2 Two-objectivemean fitness-generation

从图1、图2可知，VEGA在进化22代后y1和y2的最大适应度曲线和平均适应度曲线均达到稳定，分别反映出VEGA具有良好的收敛性和动态性。最大适应度进化曲线反映解的变化，用来评价算法的收敛性；平均适应度进化曲线用来评价遗传算法的动态性能。

两目标VEGA搜索的Pareto非劣解方案平均水平见表3。

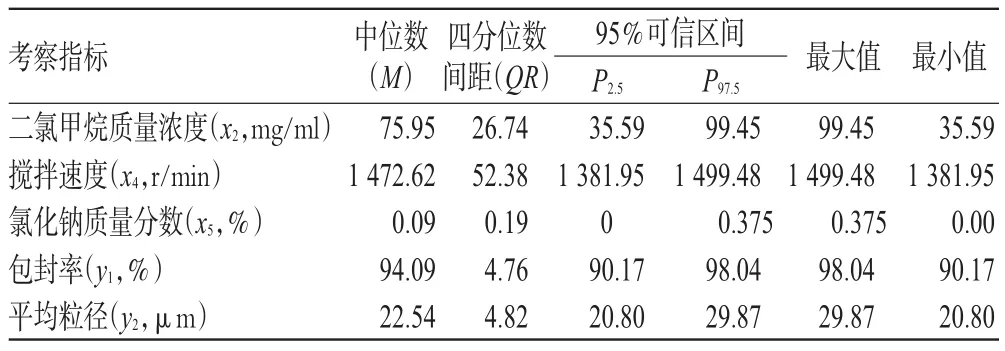
表3 两目标VEGA搜索的Pareto非劣解方案平均水平Tab 3 Average level of Pareto non-inferior solution of VEGAtwo-objective

由表3可知，12次随机搜索结果中，y195%可信区间的精度很高，其中位数为94.09%，四分位数间距为4.76%；y2的中位数为22.54µm，四分位数间距为4.82µm，95%可信区间的精度很高，由此可知VEGA的搜索结果是理想的。

2.7 VEGA两目标遗传算法与单目标搜索最优制备工艺的比较

单目标与VEGA两目标Pareto非劣解方案的比较见表4。

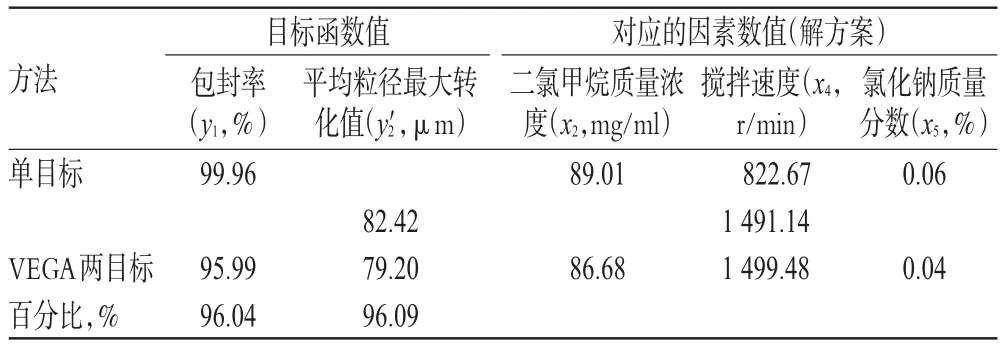
表4 单目标与VEGA两目标Pareto非劣解方案的比较Tab 4 Comparison of Pareto non-inferior solution between single-objective and VEGAtwo-objective

从表4可知，VEGA两目标遗传算法搜索的目标函数值均小于单目标搜索的函数值，目标函数值偏低正体现了多目标遗传算法的特点，因为多目标优化时将各子目标进行折中处理，尽可能获得各子目标最大的解集[1]。VEGA两目标搜索的y1达到单目标的96.04%，y2达到单目标的96.09%，VEGA遗传算法的多目标搜索的结果达到了单目标最大函数值的96%以上，结果较为满意。

2.8 VEGA两目标遗传算法与原文献最优制备工艺的比较

原文献数据利用均匀试验设计，将8次试验结果根据建立的二次回归模型中一次项、二次项的符号，得出最优制备工艺为较高的x2、较高的x4及较低的x5，并无给出具体解集，这种结论带有较强的主观性。VEGA两目标搜索出的最优工艺制备条件为y1最大达到95.99%，y2最小达到20.80µm，结果优于原文献中均匀试验设计的结果，并给出一组Pareto非劣解集，如表2中的12次随机搜索结果，可供试验者进行合理的选择。

3 讨论

VEGA搜索多目标问题时，能给出优化分析后的解集，即在因素范围内寻出一组Pareto非劣解集，这正是VEGA比原文献的优势之处。对于实际问题的方案决策，必须依据客观存在的条件，从Pareto非劣解中挑出一个或部分解作为所求大目标优化问题的最优解。结果表明：VEGA在均匀试验设计药物最优制备工艺选择的应用是满意的；确定的最优制备条件的效果较好，为研究者提供了精确度较高的试验条件方案，可推广到正交试验设计、析因试验设计的最优条件选择。

[1]仇丽霞.基于遗传算法的最优决策值选择及医药学应用研究[D].太原：山西医科大学，2007：1-3.

[2]王小平，曹立明.遗传算法-理论、应用及软件实现[M].西安：西安交通大学出版社，2001：115-117.

[3]Wu JZ，Hao XC，Chen FC，et al.A novel bi-vector encoding genetic algorithm for the simultaneous multiple resources scheduling problem[J].Journal of Intelligent Manufacturing，2012，23（6）：2255.

[4]崔逊学.多目标进化算法的研究及其应用[M].北京：国防工业出版社，2002：17-19.

[5]周建淞.基于向量评估遗传算法的多目标优化效果评价及程序测试[J].中国卫生统计，2012，29（2）：181.

[6]曹婷颖，顾月清，高向东.聚乳酸载药微球的制备和给药方法[J].药学进展，2006，30（10）：448.

[7]张海龙，高铃美，邵洪伟.聚乳酸载药微球的制备及应用研究进展[J].西北药学杂志，2010，25（2）：158.

[8]林雅铃.均匀试验设计在水溶性药物聚乳酸微球制备中的应用[J].中国医院药学杂志，2009，29（7）：531.