集成选址—路径—库存问题的逆向物流网络优化
2014-12-02李昌兵张斐敏
李昌兵,张斐敏
(重庆邮电大学 经济管理学院管理工程系,重庆 400065)
0 引言
逆向物流指在供应链管理中,生产者对从消费者处回收到的全部或部分废旧产品进行再利用、再制造或直接废弃处理的过程[1]。逆向物流系统具有高度复杂性、多样性、供应失衡性等特性,这些特性使得系统的运作更依赖于物流网络,因此在管理中的首要任务是优化设计逆向物流网络[2]。设施选址、运输线路安排和库存策略是逆向物流网络优化中的三大关键问题,传统上一般将其作为独立的决策分别进行研究[3-4]或者两两组合进行研究[5-7]。但事实上,三者之间具有密切的联系,任何一方的变动都会影响其他两方的决策。从系统的角度看,有必要对集成的“选址—路径—库存问题”(Location-Routing-Inventory Problem,LRIP)进行研究。
目前,集成的物流网络优化研究多集中在正向LRIP[8-11],只有少部分学者研究了逆向LRIP。文献[12]提出多周期的废旧汽车系统网络优化模型,该模型通过路径优化的方法计算回收的运输成本,并运用混合整数规划方法对配送进行优化,以确定最佳的处理中心位置和每周期库存数量;文献[13]建立了一个回收商管理库存模式下的多周期逆向物流网络优化模型,根据客户点的废旧产品数量决定当期是否对客户点进行回收,并设计了一种基于系统总成本最小的两阶段启发式算法进行求解;文献[14]建立了一个企业闭环物流系统中的LRIP模型,综合考虑了物流设施选址、车辆配送/回收路线安排和新产品/回收产品的库存控制等问题;文献[15]研究了垃圾回收系统的LRIP模型,集成考虑了回收中转站选址、车辆路线安排和回收中转站库存控制问题,建立了一个多周期LRIP模型。
上述逆向LRIP 模型主要存在两类不足:①多数研究仅限于独立的逆向物流系统,未将逆向物流系统与传统的物流系统有机整合在一起;②多数研究都假设回收产品当期均要回载完毕,未考虑回收产品回载的可分性。显然,利用前向配送车辆的回程来回载回收产品,比派出车辆分别进行配送和回收活动节约成本;又由于回收产品没有新产品那么强的时效性要求,可以根据实际运载能力对回收产品进行分批回收,从而降低成本。为此,本文对定位—运输路线安排问题进行扩展研究,建立了一个逆向物流的LRIP 模型。其中,在路径优化部分考虑正向配送和逆向回载相整合的运输策略,在库存控制方面考虑回收产品的可分批运输特点,引入库存限制和库存成本惩罚,以解决更加复杂的逆向物流网络布局问题,进而合理设置物流网络中的设施节点,优化运输路线,调节各节点的库存方案,从而有效降低逆向回收物流系统的运作成本。
1 模型的建立
1.1 问题描述
建立一个同时考虑正向配送和回载可分的闭环物流网络优化系统,包括若干个配送中心和相对应的客户点。每个周期各车队从配送中心出发,一一访问服务范围内的客户点,同时完成配送和回收任务,最终返回配送中心。各客户点的取/送货量不能超过车辆的载重能力,同时受冗余库存限制。根据冗余库存限制,将回收产品分为两部分:①为满足冗余库存必须回收的部分;②可当期回收也可滞留下期回收的部分。当期滞留的回收产品在客户处有库存成本。为使系统总成本最小,需要考虑的问题包括建立配送中心的数量、地址、每个周期运输车辆路径安排,以及各客户点的滞留回收产品的数量等。
1.2 假设条件
模型的假设条件如下:
(1)各类物流设施之间的距离已知。
(2)各个周期要回载的回收产品已经从单个用户回收到各客户点,不考虑单个用户到客户点之间的运输费用。
(3)各个客户点每周期新产品的需求数量和新产生的回收产品数量满足正态分布。
(4)新产品的配送必须在当期完成,而回收产品除了为满足冗余库存必须回收的部分外,剩余部分可选择部分回收或不回收。
(5)库存费用指当期未被回收的回收产品的存储费用。
(6)产品的运输费用与距离呈简单线性关系。
(7)各客户点每周期的冗余库存已知。
(8)运输车辆从配送中心发车时会产生发车费用。
1.3 模型参数和变量
(1)模型参数
N为客户点数量;
i为客户点编号(1≤i≤N);
M为候选配送中心数量;
j为配送中心编号(N+1≤j≤N+M);
g为客户点或配送中心编号(1≤g≤N+M);
h为客户点或配送中心编号(1≤h≤N+M);
K为车辆数量;
k为车辆编号(1≤k≤K);
T为计划期长度;
t为周期编号(1≤t≤T);
NQit为i客户点在t周期的新产品需求量;
RQit为i客户点在t周期新产生的回收产品数量;
Sit为i客户点在t周期末的待回收产品数量,Sit=Si,t-1+RQit-RDjtk;
Dgh为物流设施之间的距离;
Ctr为单位距离的运输成本;
Cs为单位周期单位数量的库存成本;
Fj为j配送中心的建设费用;
C为车辆的容量;
Ri为i客户点的冗余库存;
Vi为i客户点的最大库存容量。
(2)模型决策变量
NDtki为i客户点在t周期由车辆k配送的新产品数量;
RDtki为i客户点在t周期由车辆k回收的回收产品数量;

1.4 模型
根据以上分析,构建一个混合整数非线性规划的数学模型。
目标函数:

目标函数表示在满足各种约束的情况下,使系统的总成本最小。其中:第一部分表示配送中心建设成本;第二部分表示发车费;第三部分表示运输成本;第四部分表示未被回收的产品的库存成本。
约束(2)和约束(3)是车容量限制。约束(2)保证车辆k在t周期所经沿线的送货量小于车容量;约束(3)保证从该客户点回载的回收产品数量不超过当前车辆的剩余运载能力;约束(4)确保每个客户点在每周期至少被访问一次;约束(5)为线路的连续性限制;约束(6)表示车辆只能从所属的配送中心出发,且每周期内只能出发一次;约束(7)表示车辆只能服务所属配送中心对应的客户点;约束(8)必须满足每周期各客户点的配送需求;约束(9)表示回载产品数量不能超过可回载数量;约束(10)表示剩余产品数必须满足冗余库存限制。
2 算法步骤
同时考虑正向配送和回载可分的闭环LRIP模型是一个NP难题,随着问题规模的增大,可行解的数量呈指数增长,用传统的优化方法求解将非常困难。参考文献[8,16],针对所建模型的特点,本文设计了一种两阶段启发式算法:阶段一采用先“选址—分配”、后安排运输路径和库存的方法,求得满足问题约束条件的初始解;阶段二在阶段一所得初始解的基础上采用改进的搜索算法搜寻更优解。算法如下:
(1)获得初始解
步骤1 模型各参数初始化赋值,并令t=1;将各客户点分配给离其最近的配送中心,将配送中心j对应的客户点放入集合Fj(t)中;令j=N+1。
步骤2 对Fj(t)中客户点i计算bit=NQit-Pit。其中:Pit=Ri+Sit-Vi为i点在t周期必须回载的最小回收产品数量;bit为i点在t周期的正向配送数量与必须回收产品数量的差额。
步骤3 计算j回收中心在t周期的单车平均剩余量时原问 题有解;为j配送中心t周期需要的车辆数。
步骤4 将所有bit平均分成Kjt个子集θ1,θ2,…,θKjt。对每个子集都有:①为bit的标准差;②t≤T。在所有满足这种条件的子集空间中寻找一条总路径最短的子集集合,设为θ′1,θ′2,…,θ′Kjt,该集合即为综合正向和逆向物流的最优分组。
步骤5 进一步优化所得的最优子集集合。集合中的单个子集表示单个车辆所要服务的客户点集合,组内优化即相当于一个旅行商问题(Traveling Saleman Problem,TSP),而某些客户点受冗余库存限制有bit<0,因此解决TSP 问题的传统方法不完全适用于本问题。这里设计一种插入启发式算法来求解最优路径,然后运用线性规划求解最优回载配置策略。关于子集中路径和回载配置的详细优化方法请参见文献[17]。将未被回载的回收产品滞留到下一周期回收。
步骤6 令j=j+1,若j>N+M,则执行步骤7;否则执行步骤2。
步骤7 令t=t+1,若t≤T,则执行步骤2;否则执行步骤8。
步骤8 输出求得的各周期最优路径安排和回载配置方案,计算此时的配送中心建设成本、发车费、运输成本和库存成本,各项成本之和即为初始解Cost。
(2)改进初始解
步骤9 记此时被选中的配送中心数目为NUM。按照系统总成本最小原则选择关闭一个回收中心。令NUM=NUM-1,t=1,并执行步骤1~步骤8,求得此时的系统总成本,记为Cost′。
步骤10 若Cost′<Cost,则令Cost=Cost′,执行步骤11;否则直接转步骤11。
步骤11 若NUM=1,则执行步骤12;否则,返回步骤9。
步骤12 随机选择一个开放的配送中心和一个关闭的配送中心,将其状态互换,并执行步骤1~步骤8,求得此时的系统总成本,记为Cost′。
步骤13 若Cost′<Cost,则令Cost=Cost′,执行步骤14;否则令max_swap=max_swap+1,再执行步骤14。
步骤14 若max_swap>default_value,则执行步骤15;否则执行步骤13。
步骤15 算法结束,输出最终结果。
3 实验与计算
本章构建了一个闭环物流网络。该网络有5个候选配送中心(编号为1~5)和60个客户点(编号为6~65),其位置在100×100的平面随机产生,各节点之间的距离用平面坐标上的欧氏距离表示。设车容量C=600,各客户点各周期的新产品需求数NQit服从正态分布N(120,252),待回收产品数RQit服从正态分布N(100,502),单位距离运输费用Ctr=1,单位周期单位数量待回收产品的库存费用Cs=2,最大库存量Vi=200,冗余库存Ri=180,五个候选回收中心的建设费分别为Fj=(180 000,90 000,130 000,105 000,95 000),周期T=500。
采用Visual C++6.0 设计程序实现上述算法,运行环境为:3.30GHz CPU,4G 内存。得到该物流网络的最佳物流运作总成本为1 015 340,该最优解选中第2,3,4配送中心。其中:分给2号回收中心的客户点为(10,14,18,19,31,33,44,49,53,59,60,62,64),分给3 号回收中心的客户点为(9,16,21,22,27,29,35,36,37,38,41,42,43,45,46,48,50,51,54,58),分给4 号回收中心的客户点为(6,7,8,11,12,13,15,17,20,23,24,25,26,28,30,32,34,39,40,47,52,55,56,57,61,63,65)。在此以t=2时为例,给出各节点的运输路径安排和各客户点的被回载产品数量的计算结果。运输路径安排如图1所示。分别为2-10-18-14-31-33-2,2-19-60-62-53-2,2-44-49-64-59-2,3-37-50-9-16-3,3-35-43-36-46-3,3-48-27-51-21-22-3,3-58-29-45-41-3,3-38-54-42-3,4-34-6-7-55-4,4-25-57-15-4,4-47-61-39-40-32-4,4-8-28-30-13-12-4,4-24-11-56-26-63-4,4-65-52-23-20-17-4。

各客户点的回载数量如表1所示。

表1 t=2时各客户点的回载量
计算出传统模式下(正向物流活动和逆向物流活动独立进行,且回收产品当期都要回载完毕)对同一组示例数据的优化结果,并与本文提出的模型优化结果进行对比,比较结果如表2所示。从表2可以看出,前一种模式下虽然增加了客户点的库存费用,但总费用却降低了29.06%。这是因为正向物流与逆向物流的运输整合大大降低了系统的运输费用。另外,本文提出的回收产品部分回载、部分滞留的库存策略也在一定程度上减少了派车次数,降低了发车费用。
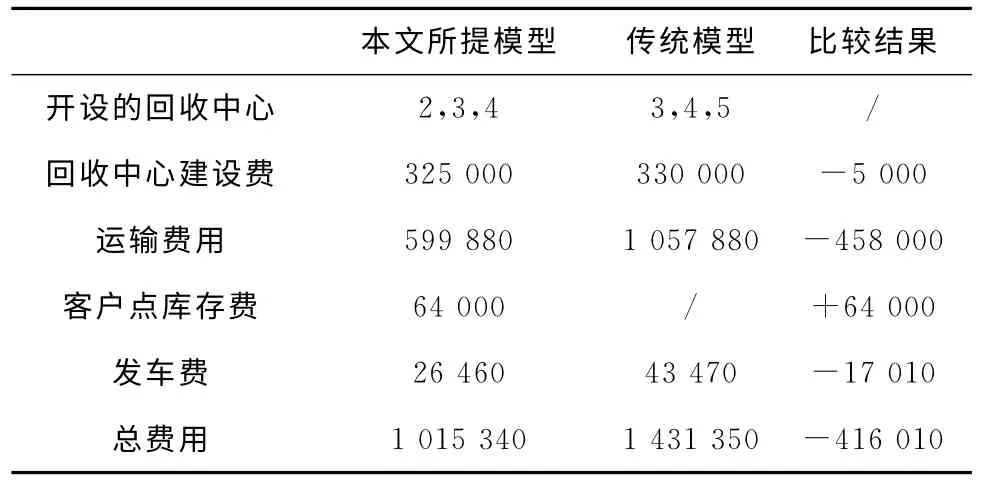
表2 不同模型优化结果对比
4 结束语
本文从逆向物流系统集成优化的角度,针对配送中心选址、车辆路径安排以及客户点的库存控制的联合决策问题,提出一个非线性混合整数规划模型,并设计了一种两阶段启发式算法来求解模型。最后通过算例验证了模型和算法的可行性。仿真结果表明,本文所考虑的正/逆向物流的运输整合和客户点的库存控制策略在优化逆向物流方面效果显著。此外,逆向物流系统存在高度的不确定性,主要体现在回收产品在数量和时间上的不确定性,同时其质量和组成成分也不确定,因此进一步的研究可考虑解决不确定环境下的逆向物流网络系统优化问题。
[1]DYCKHOFF H,LACKES R,REESE J.Supply chain management and reverse logistics[M].Berlin,Germany:Springer-Verlag,2004.
[2]DA Qingli,HUANG Zuqing,ZHANG Qin.Current and future studies on structure of the reverse logistics system:a review[J].Chinese Journal of Management Science,2004,12(1):131-138(in Chinese).[达庆利,黄祖庆,张 钦.逆向物流系统结构研究的现状及展望[J].中国管理科学,2004,12(1):131-138.]
[3]ZHOU Gengui,CAO Zhenyu.A genetic algorithm approach to location-allocation problem in reverse logistic network[J].Chinese Journal of Management Science,2005,13(1):42-47(in Chinese).[周根贵,曹振宇.遗传算法在逆向物流网络选址问题中的应用研究[J].中国管理科学,2005,13(1):42-47.]
[4]LI Bo,ZENG Chengpei.Method of multi-period dynamic location in reverse logistic network[J].Journal of Management Science in China,2008,11(5):76-84(in Chinese).[李 波,曾成培.一种逆向物流网络的多期动态选址方法[J].管理科学学报,2008,11(5):76-84.]
[5]NAGY G,SALHI S.Location-routing issues,models and methods[J].European Journal of Operational Research,2007,177(2):649-672.
[6]LIU S C,CHUNG C H.A heuristic method for the vehicle routing problem with backhauls and inventory problem[J].The International Journal of Advanced Manufacturing Technology,2005,26(4):372-381.
[7]KLEYWEGT A J,NORI V S,SAVELSBERGH M W P.Dynamic programming approximations for a stochastic inventory routing problem[J].Transportation Science,2004,38(1):42-70.
[8]LIU S C,LEE S B.A two-phase heuristic method for the multi-depot location routing problem taking inventory control decisions into consideration[J].The Inventory Journal of Advanced Manufacturing Technology,2003,22(11/12):941-950.
[9]CUI Guangbin,LI Yijun.Study on the combined location routing and inventory problem in logistics system based on bi-level programming[J].Systems Engineering—Theory &Practice,2007,27(6):49-55(in Chinese).[崔广彬,李一军.基于双层规划的物流系统集成定位—运输路线安排—库存问题研究[J].系统工程理论与实践,2007,27(6):49-55.]
[10]TAI H W,LOW C,BAI J W.Heuristic solutions to multidepot location-routing problems[J].Computer Operational Research,2002,10(29):1393-1415.
[11]WANG Yunfa,LI Bo.Research on coordinated productioninventory-distribution planning problem based on tabu search[J].Information and Control,2012,41(3):391-396(in Chinese).[王运发,李 波.基于禁忌搜索的生产-库存-配送协同计划问题研究[J].信息与控制,2012,41(3):391-396.]
[12]LEBLANC H M,FLEUREN H A,KRIKKE H R.Redesign of a recycling system for LPG-tanks[J].OR Spectrum,2004,26(2):283-304.
[13]DAI Ying,MA Zujun,ZHU Daoli.Multi-period locationrouting-inventory problem for reverse logistics with collector managed inventory[J].Industrial Engineering and Management,2010,15(5):1-6(in Chinese).[代 颖,马祖军,朱道立.回收商管理库存下逆向物流多周期LRIP[J].工业工程与管理,2010,15(5):1-6.]
[14]WANG Chanchan,MA Zujun.Stochastic dynamic location-routing-inventory problem in closed-loop logistics system for reusing end-of-use products[C]//Proceedings of the 2008International Conference on Intelligent Computation Technology and Automation.Washingtion,D.C.,USA:IEEE,2008,2:691-695.
[15]LI Huajun,MA Zujun.The stochastic location-routing-inventory problem in reverse logistics systems for municipal solid waste[C]//Logistics:The Emerging Frontiers of Transportation and Development in China.Reston,Va.,USA:ASCE,2008:3565-3571.
[16]WANG Fahong,DA Qingli.The multiple-depot &multiplevehicle transportation strategy in closed-loop chain with split pick-ups[J].Journal of Industrial Engineering/Engineering Management,2008,22(2):46-50(in Chinese).[王发鸿,达庆利.回载可分的闭环供应链多配送中心多车辆运输策略[J].管理工程学报,2008,22(2):46-50.]
[17]WANG Fahong,DA Qingli.Transportation strategy of single vehicle in reverse logistics[J].Journal of Southeast University:Natural Science Edition,2006,36(1):156-160(in Chinese).[王发鸿,达庆利.逆向物流单车运输策略[J].东南大学学报:自然科学版,2006,36(1):156-160.]
