一种基于设备运行的预防性维护与生产批量联合决策模型

张岳君，陆志强

（1.上海交通大学 机械与动力工程学院，上海 200240；2.同济大学 机械与能源工程学院，上海 201804）

0 引言

有限产能批量问题（Capacitated Lot-Sizing Problem，CLSP）在生产计划制定过程中引入设备的产能约束来保证计划的最终可行性，研究者就此提出不少扩展模型及相应算法，用以解决生产系统在不同作业环境中的产品批量决策问题［1-3］。在实际生产过程中，生产计划的最终实现还取决于设备的稳定性，故障及事后维修都将占用生产系统有限的产能资源并导致初始计划不可行，因此在生产计划决策过程中必须兼顾设备的预防性维护，以减少这些不确定性对计划的影响。同时，设备维护的费用支出在制造型企业的运营成本中占有相当高的比例［4］，将生产计划与预防性维护进行联合决策，有助于优化系统的作业安排，减少相应的成本支出。

目前生产与维护联合决策的相关研究多侧重于生产系统的调度层面［5］，从中长期层面进行两者整合研究的文献相对较少且存在一定问题。Weinstein等［6］提出基于设备运行（run-based）和基于时间间隔（interval-based）的预防性维护策略与生产计划相结合的多层次模型，两种维护策略的主要区别在于：前者的维护节点取决于设备的实际运行时间，当设备负荷不一致时可柔性调整维护周期；后者仅在设定的周期对设备进行维护，较适合设备负荷比较平稳的生产过程。Aghezzaf等［7］提出周期性预防维护与CLSP相结合的数学模型，主要采用基于时间间隔的预防性维护策略，即维护决策主要根据设备所经历的生产周期而不是周期内的实际运行时间，导致在设备负荷较低时容易造成过度维护，该联合模型和独立的维护与生产批量决策过程相比，降低的总成本不足1%。在此基础上Fitouhi等［8］提出非周期性的预防性维护与CLSP的联合模型，设备在建模过程中仍主要受生产周期的影响而非实际运行时间，与Aghezzaf等［7］的周期性维护建模方法相比，总成本降低1.5%，意味着基于时间间隔的预防性维护策略在建立联合模型中的改进效果均不明显。Aghezzaf［9］和Najid［10］等同样采用基于时间间隔的策略对生产批量和预防性维护进行联合建模研究。因为CLSP在每个生产周期的动态需求容易导致设备负荷不均衡，所以在理想状态下预防性维护计划需根据设备负荷做出相应调整，以避免设备过度维护或维护不足，故采用基于设备运行的维护策略更加合理。另一方面，上述联合模型均假设预防性维护仅在生产周期开始阶段执行，因此维护的最短时间间隔为一个生产周期，不能处理维护周期小于一个生产周期的情况，而在实际生产环境中这种情况经常出现［6］。针对以上问题，本文提出一种基于设备运行的预防性维护与生产批量的联合决策模型，同时将设备维护节点扩展到生产周期的任意范围，且允许在同一生产周期内进行多次预防性维护作业，最后引用相关文献中的算例，将本文模型与Aghezzaf［7］和Fitouhi等［8］的联合模型进行对比分析，来说明该建模方法的优越性。

1 生产批量与预防性维护的联合建模

1.1 问题描述

考虑某一单设备生产系统需在T 个生产周期内安排N 种产品的批量，设备在每个生产周期的最大产能为Kmax，第i种产品在周期t 内的需求量为dit，单位加工时间为ai，允许缺货发生。设备setup、产品生产、库存持有及缺货的单位成本分别为sit，cit，hit和bit，对应的决策变量为yit，xit，Iit和Bit。同时需要决策设备的预防性维护计划，以减少故障，提高产能的实际利用率。维护可在生产周期的任意节点进行并使设备修复如新，维护周期可以大于或小于一个生产周期，设备的状态只受其实际运行时间影响，非生产时间范围内不发生故障，生产期间发生故障时立刻进行小修并使设备修复如旧，预防性维护和遇故障小修所需的时间分别为tpm和tcm，单位成本分别为cpm和ccm。

1.2 设备的有效役龄

因为一个生产周期内最多生产N 个产品批量，所以假设一个生产周期内可最多执行N 次预防性维护，用0-1变量upt表示在生产周期t内第p 个批量之前是否执行预防性维护，用0-1 变量Ypit表示是否在第p 个预防性维护之后生产第i种产品。用τpt表示第p 个生产批量之后设备的有效役龄（effective age），即最近一次预防性维护至第p 个生产批量之间设备的累计运行时间：

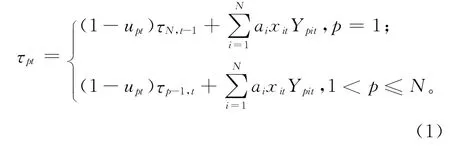
式中：（1-upt）τN，t-1和（1-upt）τp-1，t为第p 个产品批量开始时的设备役龄，表示生产第p个批量后新增的设备役龄。如果执行第p 个预防性维护（upt=1），则设备获得完全更新，之前生产过程中累积的设备役龄将归零，否则役龄将继续进行累加。同时可建立yit与Ypit之间的关系：

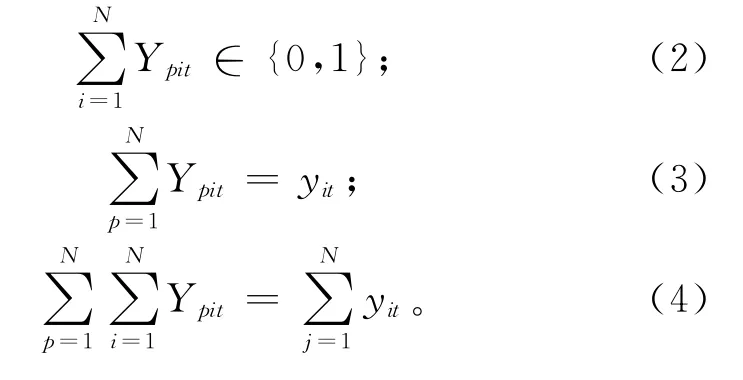
1.3 预期的故障次数和维护节点

用wpt表示周期t内第p 个产品批量生产过程中故障发生的预期次数，

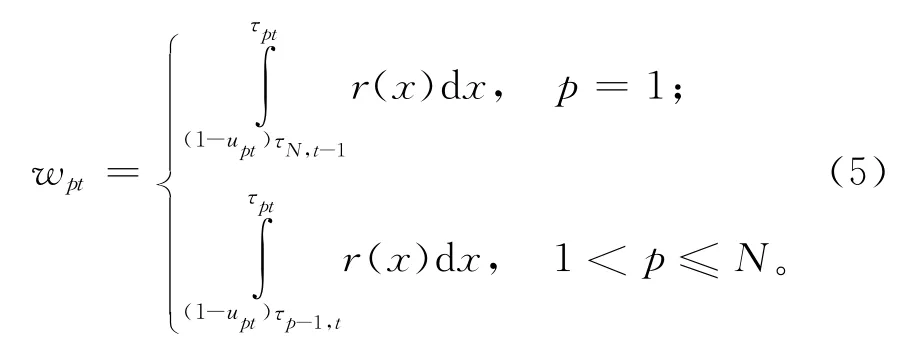
式中r（x）为设备故障率，可通过已知的故障概率密度函数f（x）进行推导。如果不考虑产品批量之间的设备闲置问题，则预防性维护的执行节点可表示为

1.4 设备的产能约束

由于设备的预防性维护与故障后的小修活动都会耗损相应的产能，一个生产周期内有效用于生产的时间将会减少，原先有限产能批量问题中的产能约束需相应调整：

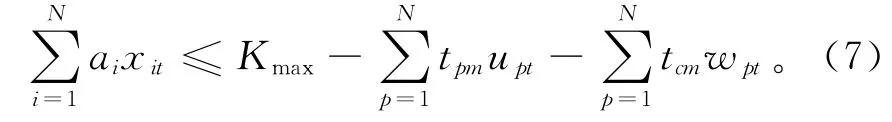
1.5 联合建模

上述生产批量和预防性维护联合决策模型（CLSP-R）可表示为：

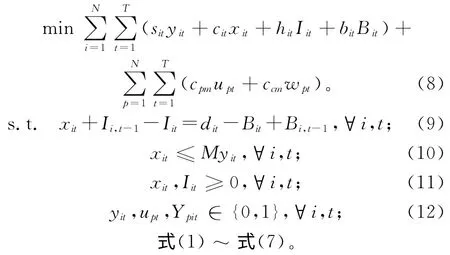
其中：联合模型的目标函数（8）是最小化生产与维护相关的总成本，式（9）是不同生产周期的物料平衡表达式，式（10）判断不同产品批量的设备调整准备操作与产量的一致性，式（11）～式（12）是对变量取值的约束，式（1）～式（7）涉及生产与预防性维护决策变量之间的相互关系。若要求预防性维护仅在生产周期开始阶段进行决策，则仅需增加每个生产周期内关于维护次数的约束

2 算例分析

将Aghezzaf等［7］和Fitouhi等［8］的联合模型分别记为CLSP-CI和CLSP-NCI，这里采用Fitouhi等［8］中的算例对三个模型进行对比，以下计算过程中用表示生产成本（PC），用表示维护成本（MC），总成本（TC）为上述两项成本之和，由于三个模型均存在非线性化表达式，采用Lingo对上述模型进行求解。

综上所述，情景教学法可以将抽象的知识更为形象地展示给学生，加深学生对知识的理解。在小学科学课堂教学中应用情景教学法，调动学生学习的积极性，增强学生学习科学知识的兴趣。将实际生活融入到教学情境中，使学生获得情感上的满足，改变以往单一、沉闷的课堂氛围。利用多媒体创设情境，丰富教学资源，可以帮助教师开展高效的教学课堂，提高学生的学习效率。

2.1 算例

假设需安排两种产品在8 个生产周期内的生产批量，表1 所示为生产两种产品的单位加工时间和生产相关的成本参数。生产设备故障服从Weibull分布，规模与形状参数分别为η=100与β=2，一个生产周期内的最大产能Kmax=50，其他设备相关的参数分别为cpm=4 000，ccm=1 000，tpm=1，tcm=4.5。

表2 所示为每个生产周期内的产品需求及CLSP-R 模型的计算结果。表3对三个联合模型的生产、维护和总成本进行了比较，因为CLSP-R 排除了设备闲置、预防性维护及小修期间的发生故障的可能性，并且增加了用于生产决策的实际产能，所以各项成本均小于其他两种建模方法。表4比较了不同建模方法条件下每个生产周期内预期的故障次数，CLSP-CI和CLSP-NCI中的故障次数主要与预防性维护计划相关，一旦维护节点确定，每个生产周期内预期的故障次数就可直接计算获得（请参阅Aghezzaf等［7］和Fitouhi等［8］的模型求解过程），而CLSP-R 中的故障个数由生产与维护计划共同决定，体现了生产与维护之间的关联性。

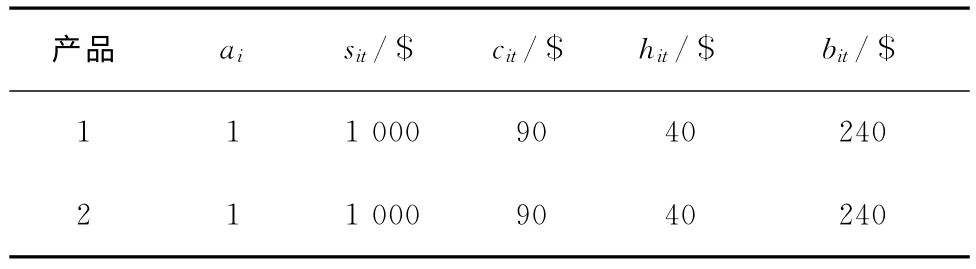
表1 生产时间和生产相关成本参数

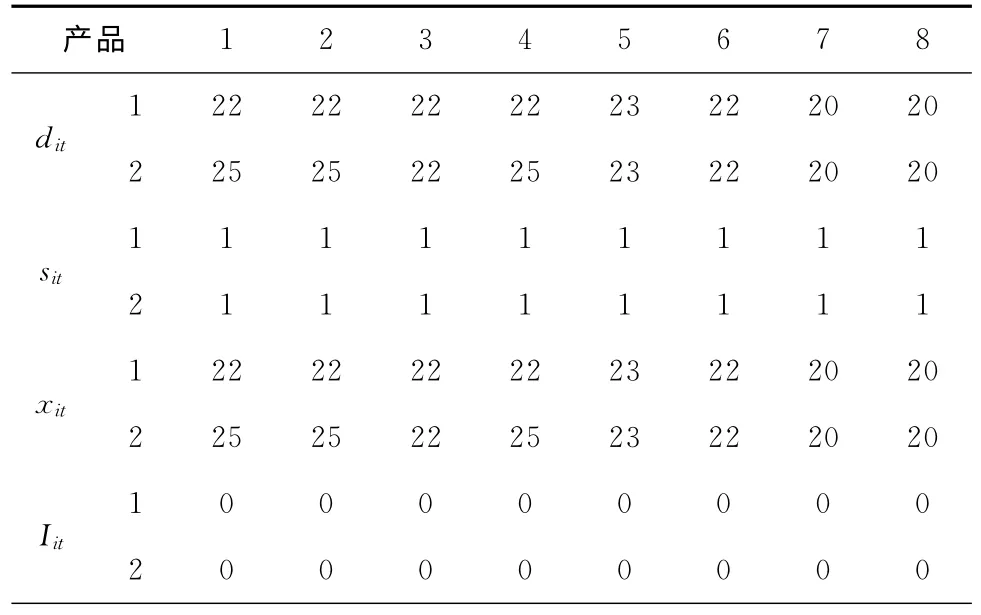
表2 产品需求及CLSP-R模型的计算结果

续表2

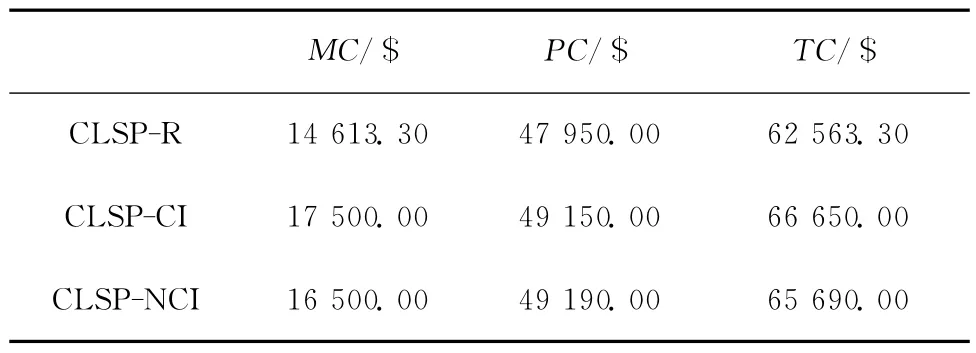
表3 生产、维护及总成本对比

表4 每个生产周期内预期的故障次数

2.2 不同设备负荷条件下的联合模型比较

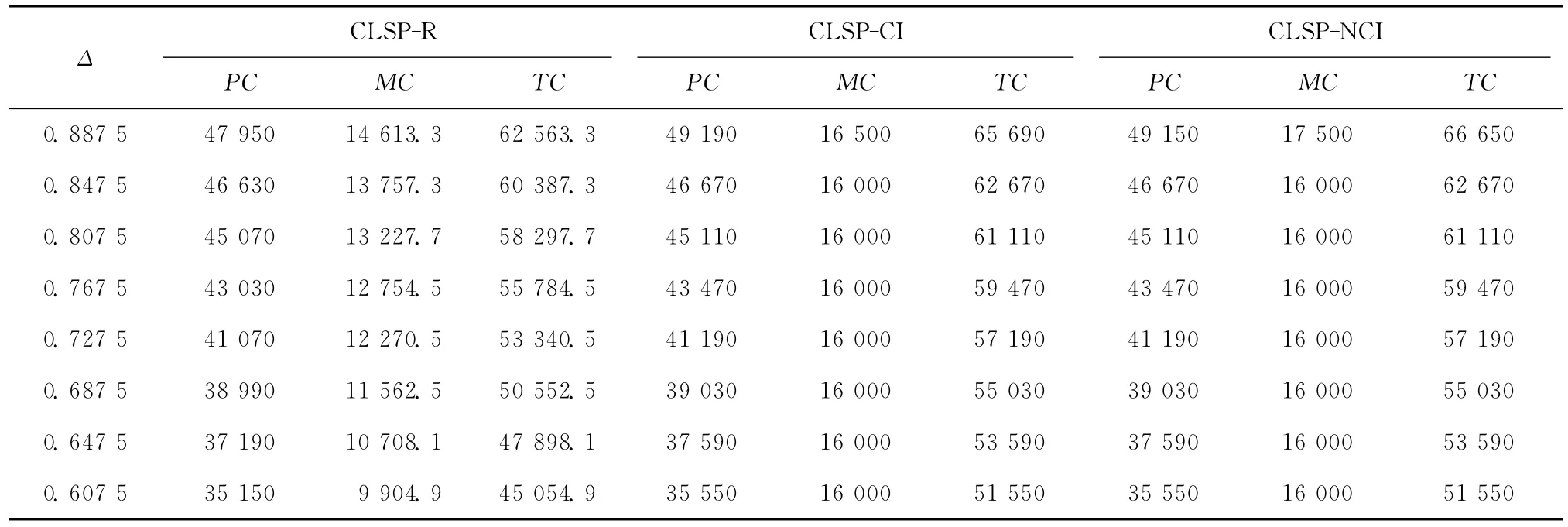
表5 不同设备负荷条件下生产、维护和总成本比较

平均维护成本是维护领域一个重要的决策依据［11］，其最优值可由最小化式（14）获得。

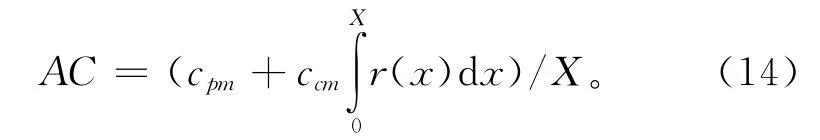
式中X 为需要决策的预防性维护周期。根据表5中的维护成本及设备累计运行时间即可计算三个联合模型的平均维护成本

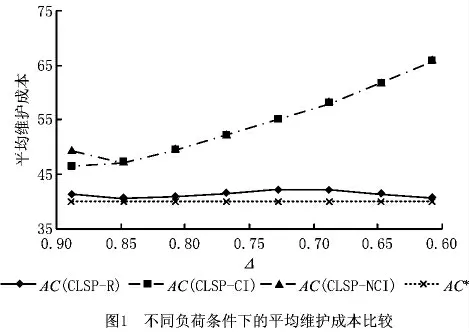
由图1可以看出，CLSP-CI和CLSP-NCI的平均维护成本随设备负荷的降低而上升，而CLSP-R的平均维护成本在不同设备负荷条件下均与最优值（AC＊）较为接近，表明基于设备运行维护策略可以随生产负荷的变化动态调整维护计划，从而降低相应的维护成本。

2.3 不同η 条件下联合模型的比较

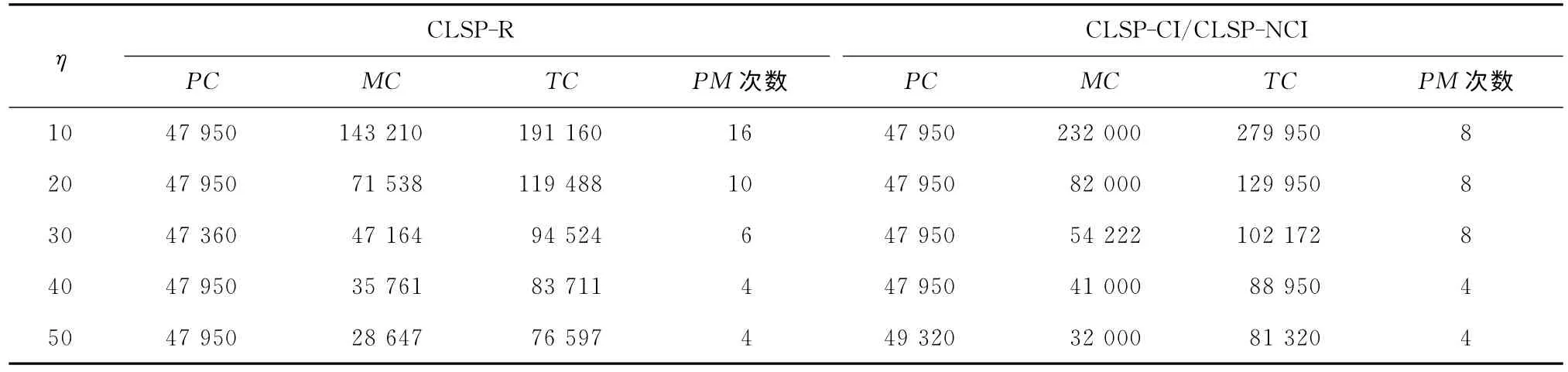
表6 不同η 条件下生产、维护和总成本比较

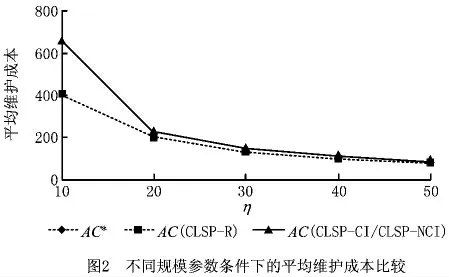
3 结束语

一般而言，设备的实际运行时间是评估设备状态和相应预防性维护决策的重要依据，因此本文提出一种基于设备运行的预防性维护和生产批量联合模型，排除了设备闲置等因素对设备状态的影响，同时假设预防性维护可以在生产周期的任意节点执行，解决了维护周期小于一个生产周期的情况。算例表明，与采用基于时间间隔预防性维护策略的建模方法相比，本文所提联合模型有助于同时减少生产与维护成本，避免设备过度维护及维护不足的问题，而平均维护成本与最优值较为接近的事实验证了该联合模型的有效性。

与单设备问题相比，多阶段生产系统（如流水线）在制造型企业中更为常见。由于包含了设备之间的缓冲区间、在制品及不同设备的维护关联性，这类不可靠系统的运行机制、产能评估与数学建模更为复杂，进一步考虑将设备维护对系统微观层面运作的影响反馈到宏观的批量决策中，从而有助于这类复杂系统生产计划制定的科学性与可行性，这对多阶段生产系统的绩效研究也是很有意义的拓展。

［1］JANS R，DEGRAEVE Z.Meta-heuristics for dynamic lot sizing：a review and comparison of solution approaches［J］.European Journal of Operational Research，2007，177（3）：1855-1875.

［2］KARIMI B，GHOMI S M T，WILSON J M.The capacitated lot sizing problem：a review of models and algorithms［J］.Omega，2003，31（5）：365-378.

［3］QUADT D，KUHN H.Capacitated lot-sizing with extensions：a review［J］.A Quarterly Journal of Operations Research，2008，6（1）：61-83.

［4］ALSYOUF I.Maintenance practices in Swedish industries survey results［J］.International Journal of Production Economics，2009，121（1）：212-223.

［5］MA Y，CHU C，ZUO C.A survey of scheduling with deterministic machine availability constraints［J］.Computers &Industrial Engineering，2010，58（2）：199-211.

［6］WEINSTEIN L，CHUNG C H.Integrating maintenance and production decisions in a hierarchical production planning environment［J］.Computers &Operations Research，1999，26（10／11）：1059-1074.

［7］AGHEZZAF E H，JAMALI M A，AIT-KADI D.An integrated production and preventive maintenance planning model［J］.European Journal of Operational Research，2007，181（2）：676-685.

［8］FITOUHI M C，NOURELFATH M.Integrating noncyclical preventive maintenance scheduling and production planning for a single machine［J］.International Journal of Production Economics，2012，136（2）：344-351.

［9］AGHEZZAF E H，NAJID M N.Integrated production and preventive maintenance in production systems subject to random failures［J］.Information Sciences，2008，178（17）：3382-3392.

［10］NAJID M N，ALAOUI-SELSOULI M，MOHAFID A.An integrated production and maintenance planning model with time windows and shortage cost［J］.International Journal of Production Research，2011，49（8）：2265-2283.

［11］WANG H.A survey of maintenance policies of deteriorating systems［J］.European Journal of Operational Research，2002，139（3）：469-489.