基于亲和度的改进引力搜索算法

周少武，陈 微，唐东成，张红强，王 汐，周 游

(1.湖南科技大学信息与电气工程学院，湖南 湘潭 411201;2.湖南大学电气与信息工程学院，长沙 410082)

1 概述

在工程实践中，许多问题都涉及优化，如成本最低问题、距离最短问题、电力系统中无功补偿配置问题等。而启发式搜索算法就是解决优化问题的一类方法，它不同于经典的数学算法。这些启发式搜索算法是受大自然现象和运动规律启发得到的，如萤火虫算法［1］、人工鱼群算法［2］、粒子群算法［3］等。这些算法已被事实证明，它们能解决复杂的非线性的优化计算问题，因此，在各个领域得到广泛的应用。值得指出的是，对于所有函数集合，并不存在万能的最佳优化算法［4］，某种算法可能解决某些函数极值的求解，因此，启发式算法的研究是一个开放性的问题。

引力搜索算法(Gravitational Search Algorithm，GSA)［5］是由伊朗的克曼大学教授Esmat Rashedi 等人于2009 年提出的。GSA 算法思想来源于牛顿万有引力定律，它通过群体中各粒子之间的万有引力相互作用产生的群体智能指导优化搜索［6］。它从可行域中随机地产生一组初始解，且把它们看成是带有一定质量的粒子，这个质量决定了粒子对种群中其他粒子吸引的强弱——质量越大，吸引能力就越强;反之，质量越小，吸引力越小，之后求出合力、加速度，再对粒子进行速度、位置更新。

引力搜索算法是一个新兴的算法，在文献［7］中证明GSA 的收敛性明显优于粒子群算法［8］和遗传算法等其他智能算法，同时引力搜索概念简单、容易实现，而且需要调整的参数少。自从GSA 提出以来，从不同的方面对其进行了改进，如文献［9］将宇宙中的黑洞操作引入到GSA，在解决单峰函数问题时效果很好，文献［10］将GSA 推广至离散时间系统，提出了一种快速离散的GSA 算法。本文受到文献［11］对类电磁机制改进的启发，通过引入亲和度概念来改进GSA。

2 基本引力搜索算法

假设在搜索空间中，每一个粒子的位置用如下向量表示:

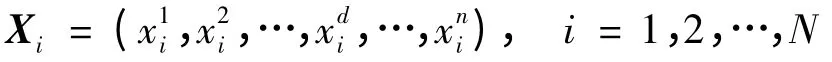
其中，N 表示种群数量;xdi 表示第i 个粒子在第d 维的位置。

根据如式(1)和式(2)计算出粒子的惯性质量并得出质量的归一化:

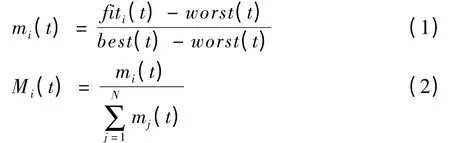
对于最小值问题，best(t)和worst(t)的定义为:

对于最大值问题，best(t)和worst(t)的定义为:

其中，fiti(t)是粒子i 在t 时刻的适应度值。

接着根据式(7)可以计算各个粒子在每一维空间上的引力，在第d 维上第i 个粒子与第j 个粒子之间的万有引力为:

G(t)是引力系数，它随时间而递减:

其中，G0和α 为时间常数;T 为最大迭代次数。

在引力搜索算法中，为了增加算法随机特性，认为第d 维作用在第i 个粒子上总的作用力来自其他所有粒子作用力的总和，其大小定义如下:

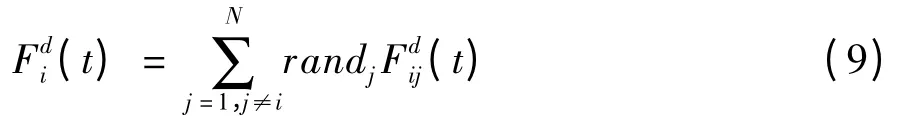
其中，randj是范围在［0，1］之间的随机数。

根据牛顿第二定理，第i 个粒子在第d 维上t 时刻的加速度定义如下:

其中，Mi(t)是第i 个粒子在t 时刻的惯性质量。

最后根据式(11)和式(12)更新粒子的速度和位置:

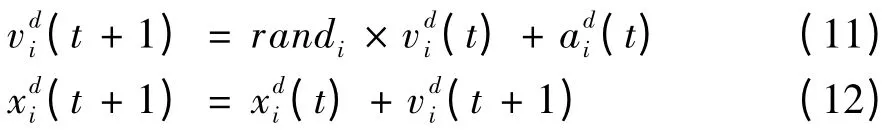
其中，randi为［0，1］的随机数。

3 改进的引力搜索算法

3.1 算法分析

引力搜索算法的关键在于粒子质量的计算，粒子质量是由适应度来衡量的，适应度越好，粒子质量越大，对作用粒子的吸引力越大，使作用粒子偏向粒子质量大的运动。对于群体，作用粒子将受到群体粒子质量的影响，从而产生一个合力，影响作用粒子的最优方向。

根据以上过程可知引力与粒子的质量(或函数的适应度)息息相关。因此，通过改变粒子的引力合力计算公式来对引力搜索算法进行改进。

3.2 改进的合力公式

根据上文对算法的分析，在式(9)中添加了一个系数λ 来修正算法中的合力公式。系数λ 的计算公式为:

其中，λ 为式(9)需要添加的系数;k1，k2为可调整参数，可以根据不同函数设置;C 为参数，与k2有关，即y(x)为一分段函数，它由x 得来，通过式(14)可以使y(x)在［0，π×2-1］内变化，x 的计算由式(13)得到，其中，M(i)和M(j)分别为粒子i 和粒子j 的质量;x 的作用是对函数值进行亲和度检测。x 值越小即2 个粒子的质量值的差越小，表示其亲和度越大，且两者之间的引力越大;反之，两者之间的引力就越小。此关系通过式(15)体现出来，因此，将上式代入式(9)得到改进的合力计算公式为:

从式(16)可以看出，通过添加λ 改变合力表达式，可以加快粒子向最优方向运动。

由于粒子的质量是由目标函数适应度值确定的，其目标函数适应度值的大小越接近，粒子质量的大小也越接近，进而使得的值越小，代入式(15)得到一个系数λ 的值，且由式(15)可以看出，x 越小，λ 的值越大，其亲和度越大，进而使得两粒子间的引力也越大。故由上述分析可得，粒子间目标函数适应度值越接近，粒子间的引力也越大，从而在理论说明可以加快种群的收敛速度。

3.3 改进的算法流程

改进的搜索算法流程如下:

(1)搜索空间的识别，确定问题的搜索空间。

(2)随机初始化粒子的位置，最大迭代次数T，初始化种群N。

(3)对每个粒子根据目标函数计算粒子的适应度值。

(4)根据式(8)计算更新引力函数G(t)，根据式(1)和式(2)计算更新每个粒子的质量M(t)。

(5)根据式(7)计算每个粒子间的引力。

(6)根据式(13)计算各粒子质量差。

(7)根据式(14)映射到区间［0，π/2］。

(8)根据式(15)计算得到系数，并代入式(16)得到粒子受到的合力。

(9)根据式(10)和式(11)分别计算粒子的加速度和速度。

(10)根据式(12)更新每个粒子的速度。

(11)重复步骤(3)～步骤(8)直至满足算法条件，结束。

4 仿真实验

本文仿真实验在Windows 8 系统和Matlab 2012a 下，进行并采用了5 个经典测试函数去验证算法的有效性，在此算法中先初始化:G0=100，α=20，T=1 000，种群数N=50，维数30。计算所得的结果是求取其30 次平均值，所选择的测试函数如表1 所示，均为最小化问题，最小值都为0。

表1 测试函数

在表1 中，f1为Sphere 单峰二次函数，主要用来测试算法寻优精度;f2为Rosenbrock 函数，是一个非凸、病态函数;f3为Rsatrigin 函数，多峰，在S={xi∈(-5.12，+5.12)，i=1，2，…，n}范围内大约存在10n个局部极小点，一般算法较难得到全局最优解;f4为Ackley 函数，是一个具有深度局部最小点的多峰函数;f5为Griewank 函数，多峰，存在大量局部极小点。f3～f5主要用来检验算法全局搜索的性能和避免早熟。

测试结果如表2 和表3 所示。其中，表2 是式(14)和式(15)中的可调参数，是在实验所得结果和收敛性最好的情况下整定得到的。表3 分别为基本GSA、改进GSA(PGSA)、文献［12］的MGSA 和文献［13］的GSAGJ 所得到结果的平均值。

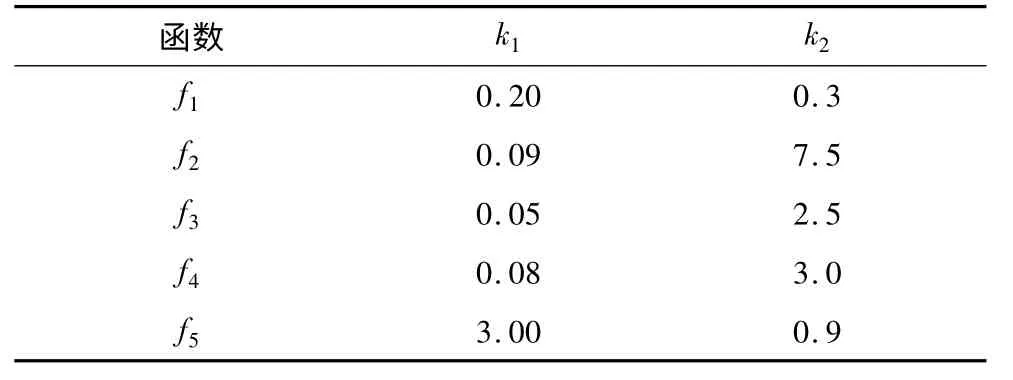
表2 可调参数值

表3 结果平均值

图1～图5 为函数f1～f5的仿真实验曲线。

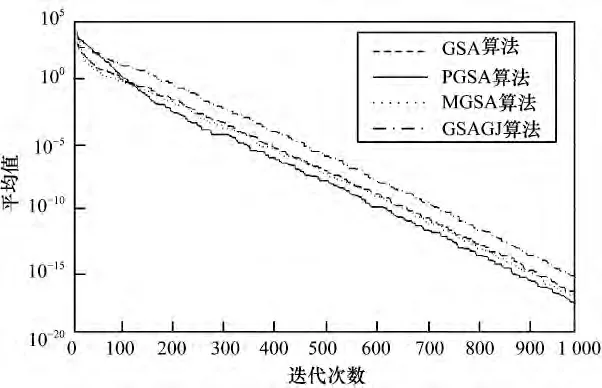
图1 f1函数的进化曲线

图2 f2函数的进化曲线

图3 f3函数的进化曲线

图4 f4函数的进化曲线

图5 f5函数的进化曲线

实验结果分析如下:

(1)由表3 和图1 可知，对于复杂的单模态函数Sphere，PGSA 算法的收敛速度比MGSA 稍快、比GSA 快、比GSAGJ 快得明显。另外，PGSA 收敛精度高，MGSA 次之，同时可以看到，GSAGJ 在求单模态函数Sphere 时不是很好。

(2)对于Rosenbrock 函数，由图2 可以看出，PGSA 算法进化到100 代左右就开始收敛，MGSA 和GSA 均到200 代左右收敛，GSAGJ 到300 代以后才开始收敛，搜索精度相当。

(3)Griewank、Ackley、Rsatrigin 等3 个多模态函数均是复杂的非线性全局优化问题，主要用来测试算法的全局搜索性能［14］，从图3～图5 和表3 可以看出，3 种改进GSA 算法的优化效果均比GSA 好。对于3 个函数，PGSA 算法的收敛速度均高于GSA、MGSA 和GSAGJ 算法。对于Griewank 函数，MGSA算法比其他3 种算法搜索的结果都要好，但PGSA 收敛速度最快，在100 代左右就收敛到了最优值。GSAGJ 算法在收敛精度和收敛速度方面都很不理想，只比GSA 稍好。对于Ackley 函数，PGSA 也能几乎线性收敛，且收敛速度最快，GSAGJ 算法次之，都比GSA 要好。在收敛精度方面，3 种改进算法均优于GSA，其中PGSA 算法最好，GSAGJ 算法稍差，PGSA 算法仅比GSA 好。对于Rsatrigin 函数，在3种改进的GSA 算法中，PGSA 无论在收敛速度还是在收敛精度方面都有绝对的优势，并且达到了理论最优值，GSAGJ 次之，MGSA 比GSA 要好。

通过以上算法改进的理论叙述与仿真实验的结果可知，粒子在搜索解的过程中是不断寻优的，每一个粒子受到来自各个不同质量吸引力的作用，从而产生一个合力，并在这个合力的作用下运动，通过引进粒子质量差，发现质量大的粒子与质量小的粒子，由于其质量差较大，亲和度小，因此它们间的引力小，这样就会减小质量小(即劣解)的粒子对质量大的粒子的作用力，从而减小质量大的粒子所受的合力对最优解的偏差，进而使粒子能更好地朝着所期望即最优的方向运动，这样不仅加快了收敛速度，而且能提高搜索精度。总之，PGSA 在函数优化时有它的有效性和优势。

5 结束语

本文提出了一种基于亲和度的改进引力搜索算法。通过引入质量差来检测粒子间的亲和度，如式(13)所示，然后通过式(14)～式(15)构造了一个系数添加到合力计算表达式中，通过亲和度的大小来反映粒子间适应度的关系，从而反映出粒子间的引力大小，质量差越小，亲和度越大，粒子间引力越大，产生的速度快;反之，质量差越大，亲和度越小，粒子间引力越小，产生的速度越小。仿真实验表明，改进的GSA 算法提高了算法的收敛速度和搜索精度。然而，针对更为复杂的函数，本文算法在寻优速度和精度方面还有待提高。

［1］Krishnanand K N，Ghose D.Detection of Multiple Source Locations Using a Glowworm Metaphor with Applications to Collective Robotics［C］//Proc.of Swarm Intelligence Symposium.［S.l.］:IEEE Press，2005:84-91.

［2］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式:鱼群算法［J］.系统工程理论与实践，2002，22(11):32-38.

［3］Kennedy J.Particle Swarm Optimization［C］//Proc.of IEEE International Conference on Neural Networks.Perth，Australia:IEEE Press，2010:760-766.

［4］江铭炎，袁东风.人工鱼群算法及其应用［M］.北京:科学出版社，2012.

［5］Rashedi E，Nezamabadi-Pour H，Saryazdi S.GSA:A Gravitational Search Algorithm［J］.Information Sciences，2009，179(13):2232-2248.

［6］杨 晶，黎 放，狄 鹏.免疫万有引力搜索算法的研究与仿真［J］.兵工学报，2012，33(12):1533-1538.

［7］Li Chaoshun，Zhou Jianzhou.Parameters Identification of Hydraulic Turbine Governing System Using Improved Gravitational Search Algorithm［J］.Energy Conversion and Management，2011，52(1):374-381.

［8］李 沛，段海滨.基于改进万有引力搜索算法的无人机航路规划［J］.中国科学:技术科学，2012，42(10):1130-1136.

［9］Doraghinejad M，Nezamabadi-pour H，Hashempour S A，et al.A Hybrid Algorithm Based on Gravitational Search Algorithm for Unimodal Optimization［C］//Proc.of the 2nd International Conference on Computer and Knowledge Engineering.Mashhad，Iran:IEEE Press，2012:129-132.

［10］Shamsudin H C，Irawan A，Ibrahim Z，et al.A Fast Discrete Gravitational Search Algorithm［C］//Proc.of the 4th International Conference on Computational Intelligence，Modelling and Simulation.Kuantan，Malaysia:IEEE Press，2012:24-28.

［11］姜建国，王双记，刘永青，等.一种实用的类电磁机制算法［J］.西安电子科技大学学报:自然科学版，2013，40(2):59-64.

［12］李春龙，戴 娟，潘 丰.引力搜索算法中粒子记忆性改进的研究［J］.计算机应用，2012，32(10):2732-2735.

［13］徐 遥，王士同.引力搜索算法的改进［J］.计算机工程与应用，2011，47(35):188-192.

［14］胡超杰，章 兢.一种采用选择的免疫差分进化算法［J］.计算机应用研究，2013，30(6):1640-1651.